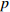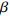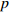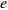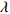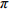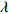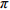The Incentive Contract of Community Supported Agriculture Based on Consumer Risk Aversion
-
摘要:
研究社区支持农业体系中投资型消费者的风险规避度对生鲜农产品公司收益和决策以及其合作机制的影响。构建了新鲜度和价格共同影响的需求函数和风险规避的投资型消费者效用函数,以及生鲜农产品公司和投资型消费者的收益共享函数,通过求解得到完全和不完全信息情况下最优的分红比例、投入的保鲜努力以及各参与者的利润,并对其进行了数值仿真。发现在完全信息情况下,存在帕累托最优结果;在不完全信息情况下,存在均衡解且随着投资型消费者风险规避度的增加,消费者的收益逐渐减少,公司的收益和投入的保鲜努力都增大。在面对风险规避的消费者时,其风险规避度越大公司应投入的保鲜努力也越大,以此来保证和消费者的长久合作,保障社区支持农业的发展。
Abstract:To study the impact of risk aversion of investment consumers on the profits and decision-making of fresh agricultural products companies and their cooperation mechanismin in the community supported agriculture system. The demand function impact by freshness and price and the utility function of risk-averse investment consumers and the revenue sharing function of fresh agricultural products companies and investment consumers are constructed. The optimal profits sharing ratio, preservation effort and profit of each participant under the condition of complete and incomplete information were obtained. And its numerical simulation is carried out. It is found that Pareto optimal results exist under complete information. In incomplete information, there is an equilibrium solution.With the increase of risk aversion of investment consumers, the profits of consumers gradually decrease, while the profits of companies and the preservation efforts of investment increase. In the face of risk-averse consumers, the more risk-averse the consumers are, the more efforts company should invest in preservation, to ensure long-term cooperation with consumers and the development of community-supported agriculture.
-
近年来层出不穷的食品安全事故,让传统的农产品供销方式在消费者心中失去信誉。国家对农业现代化及城乡生态文明的大力倡导,“社区支持农业”(community supported agriculture, CSA)以其保障食品安全、保护生态环境、促进区域发展等作用成为企业、学术界关注的焦点。Lamb[1]将CSA定义为生产者与消费者之间建立的以社区为导向的农产品供销组织,消费者为生产者提供预先的资金支持,生产者负责供应足量和优质的食品以满足消费者的需求,其核心理念是“风险共担、收益共享”。
从2008年石嫣博士建立我国第一个CSA项目起,国内已有超过500个CSA项目[2]。目前,国内外对CSA的研究都集中在发展前景和发展模式、发展方式的探究以及如何建立消费者信任方面[3-5]。学者们普遍认为CSA的消费者具有收入高、受教育程度高、多居住在城市的特点[6-9]。在我国,CSA正处于初期阶段,研究主要集中于如何使CSA项目成功运营[10-11]。学者们对CSA在环境、社会、经济方面发挥的效益普遍持肯定态度,但CSA在本土化中依然存在很多问题[12-13]。付会洋等[14]指出,我国发展CSA面临管理、人才、生产、消费和土地5个方面的困境。
以委托代理机制为背景的农业发展激励机制研究都集中在农产品供应链协调和供应链的特性、定价和补货等管理策略的研究上。王磊等[15]以消费者效用函数为基础,建立两级生鲜农产品供应链利润模型,设计两种促进供应商提高保鲜努力的激励机制。杨果等[16]基于多任务委托代理模型,设计政府激励和约束新型农业经营主体参与低碳农业发展的激励机制。由于农产品的特殊属性,农产品供应链风险规避问题也成了近年来学者们的重要研究对象。郑琪等[17]研究生鲜农产品新鲜度和风险偏好程度对供应链利润的影响,探讨生鲜农产品投入质量安全科技因素后供应链利润的变动趋势。Sheng等[18]设计风险偏好投资人的激励机制,解决农产品龙头企业和投资者之间的信息不对称问题。曲优等[19]研究风险规避生产商绿色投资策略选择的演化过程、演化路径及其影响因素。江世英等[20]考虑风险规避度和产品绿色度、消费者偏好等因素,探讨风险规避度对制造商和零售商效用的影响。
我国农产品供应无论在消费端还是生产端,力量都比较分散,CSA中生产者和消费者的对接必须要依赖生鲜农产品公司,但以CSA为背景研究生鲜农产品公司的文章少之又少。因此本文以CSA为背景,建立以风险规避消费者的效用为基础的委托代理模型。CSA中消费者又是公司投资人,具有不同风险规避度的消费者投资选择具有差异。本文将生鲜农产品的产品新鲜度及消费者的风险规避程度融入到合作契约的设计中,设计合理的契约激励生鲜农产品公司努力提高保鲜水平,并为公司提供面对风险规避的消费者可采取的策略,以期为CSA中生鲜农产品公司的管理提供理论依据。
1. 问题与假设
本文研究由农户、一个风险中性的生鲜农产品公司和风险规避的消费者组成的CSA体系。农户负责生产优质的生鲜农产品;公司承担运输生鲜农产品和运营,协调整个CSA的工作;消费者提前支付一笔用于农户生产、公司运营的费用,在农产品成熟时,消费者不仅能得到一定量的生鲜农产品,还可以得到销售农产品收益分红。本文中消费者既是购买农产品的客户,又是公司的投资人、收益共享人,称为投资型消费者。本文假设如下。
1) 本文研究投资型消费者作为委托人对代理人生鲜农产品公司的激励机制。消费者具有一定的风险规避度,本文用均值−方差理论表示其效用函数
${U_1}$ 。${U_1} = E({\pi _1}) - \lambda {\rm{Var}}({\pi _1})$ 。其中,$\lambda $ ($\lambda {\text{>}} 0$ )表示消费者的风险规避度,$\lambda $ 值越大表示对风险越规避;${\pi _1}$ 表示消费者的收益。2) 生鲜农产品的新鲜度随时间递减,即
${\theta _t}{\rm{ = }}\theta _0^{t}$ ,其中,0<${\theta _0}$ <1。若公司对生鲜农产品进行保鲜,可减缓其新鲜度衰减,但即使公司投入最大的保鲜努力也仍然无法使生鲜农产品新鲜度高于${\theta _0}$ 。因此,将投入保鲜努力后农产品的新鲜度函数设为${\theta _t}{\rm{ = }} \theta _0^{{t}}{\rm{ + }}{k_1}e$ 。其中,$e \in (0,1)$ 表示生鲜农产品公司所付出的保鲜努力水平;$ {k}_{1}\in (0,1-{\theta }_{0})$ 表示保鲜努力对保鲜效果的影响。3) 生鲜农产品公司投入保鲜努力必须付出相应的保鲜成本,设保鲜成本函数为
${C_1}{\rm{ = }}\dfrac{1}{2}{k_2}{e^2}$ 。其中,${k_2}$ >0表示保鲜努力水平对保鲜成本的影响系数,该式表明公司投入保鲜努力水平越高,付出的保鲜成本越高。4) 消费者在购买生鲜农产品时,往往会对生鲜农产品的新鲜度进行判断,并将此作为是否购买的依据。假设消费者同时对生鲜农产品的价格和新鲜度敏感,新鲜度与价格共同影响消费需求,即市场需求率为
$q{\rm{ = }}(a - bp{\rm{)}}{\theta _t}$ 。其中,$a$ 表示市场潜在规模;$b$ 表示消费者对价格的敏感系数;$p$ 表示生鲜农产品的价格。文中使用的其他符号含义如下:
$T$ 表示生鲜农产品的销售周期;$D$ 表示生鲜农产品的需求量;$\varepsilon $ 表示需求的不确定性$\varepsilon \in N(0,{\sigma ^2})$ ;$\beta $ 表示生鲜农产品公司的收益共享系数;${V_1}$ 表示消费者投资金额;${V_2}$ 表示生鲜农产品公司给农户的质量奖励;$ {\pi }_{1}(\beta ,e)$ 表示投资型消费者收益;${\pi _2}(\beta ,e)$ 表示生鲜农产品公司收益;${U_1}(\beta ,e)$ 表示投资型消费者效用;${U_2}(\beta ,e)$ 表示生鲜农产品公司效用。2. CSA合作模型
由假设4可知,一个销售周期T内生鲜农产品的总需求量为
$$\begin{split} &\qquad D = \int_0^T {q{\rm{d}}t} + \varepsilon = \int_0^T {(a - bp)} (\theta _0^{{t}}{\rm{ + }}{k_1}e){\rm{d}}t + \varepsilon = (a - bp) \times \\&\left(\frac{{\theta _0^T - 1}}{{\ln {\theta _0}}} + {k_1}eT\right){\rm{ + }}\varepsilon{\textit{。}} \end{split} $$ 则投资型消费者的利润函数为
${\pi _1}(\beta ,e){\rm{ = }}(1 - \beta )$ $(p - w)\times D - {V_1} $ ,期望利润和方差为$E({\pi _1}) = (1 - \beta )(p - w)$ $(a - bp)\left(\dfrac{{\theta _0^T - 1}}{{\ln {\theta _0}}} + {k_1}eT\right) - {V_1}$ ,${\rm{Var}}({\pi _1}) = E{({\pi _1} - E({\pi _1}))^2} = (1 - \beta {)^2} \times$ ${(p - w)^2}{\sigma ^2}$ 。根据假设1,利用均值−方差理论得到的投资型消费者效用函数为
$$\begin{split} &\qquad{U_1}(\beta ,e) \;=\; E({\pi _1}) \;-\; \lambda {\rm{Var}}({\pi _1}) = (1 - \beta )(p - w)(a - bp) \times\\& \left(\frac{{\theta _0^T - 1}}{{\ln {\theta _0}}} + {k_1}eT\right) - {V_1} - \lambda {(1 - \beta )^2}{(p - w)^2}{\sigma ^2}{\textit{。}} \end{split}$$ 生鲜农产品公司的利润函数为
${\pi _2}(\beta ,e) = \beta (p - w)D + {V_1} - {V_2} - {C_1}$ ,期望利润和效用分别为$$ \qquad E({\pi _2}) = \beta (p - w)(a - bp)\left(\frac{{\theta _0^T - 1}}{{\ln {\theta _0}}} + {k_1}eT\right) + {V_1} - {V_2} - \frac{1}{2}{k_2}{e^2};$$ $$ \begin{split} &\qquad{U_2}(\beta ,e) = \beta (p - w)(a - bp)\left(\frac{{\theta _0^T - 1}}{{{\rm{ln}}{\theta _0}}} + {k_1}eT\right) + {V_1} - {V_2} -\\[-5pt]& \frac{1}{2}{k_2}{e^2}{\textit{。}} \end{split}$$ 基于以上,投资型消费者−生鲜农产品公司的合作模型为
$$\qquad\begin{array}{l} {\rm{max}}\;{U_1}{\textit{。}} \\ {\rm{s.t}}\;\left\{ \begin{array}{l} ({\rm{IR}})\;{U_2} \geqslant 0 {\textit{;}}\\ ({\rm{IC}})\;{e^{\rm{*}}} \in {\rm{argmax}}{U_2}(e) {\textit{。}}\\ \end{array} \right.\; \\ \end{array} $$ IR指参与约束,只有生鲜农产品公司的效用大于零时,生鲜农产品公司才会加入CSA项目中;IC是激励相同约束,是对生鲜农产品公司投入保鲜努力的约束,即在任何情况下生鲜农产品公司都会选择投入最优的保鲜水平。
2.1 完全信息下CSA合作模型
在完全信息情况下,投资型消费者可以观测到生鲜农产品公司投入的保鲜努力。这时IC不起作用,公司通过满足IR来实现最优的合作契约。所以,上述合作模型为
$$\begin{split} &\qquad \max\; \left( {(p - w)(a - bp)(\frac{{\theta _0^T - 1}}{{\ln {\theta _0}}} + {k_1}eT) - {V_2} - \frac{1}{2}{k_2}{e^2} - \lambda (1 - } \right.\\& \Biggr. {\beta {)^2}{{(p - w)}^2}{\sigma ^2}} \Biggr){\textit{。}} \end{split}$$ 根据求导法则分别对
$e$ 和$\beta $ 求导,得到${e^*} = \dfrac{{(p - w)(a - bp){k_1}T}}{{{k_2}}}$ ,$\;{\beta ^{\rm{*}}}{\rm{ = 1}}$ 。将${e^*}$ 、$\;{\beta ^{\rm{*}}}$ 代入IR中,可以得到消费者最优投资为$$\qquad{V}_{1}^{\rm{*}} = {V}_{2} - (p - w)(a - bp) \left[\left(\frac{{\theta }_{0}^{T}-1}{\mathrm{ln}{\theta }_{0}}\right) - \frac{{k}_{1}^{2}{T}^{2}(p-w)(a-bp)}{2{k}_{2}} \right] {\textit{。}}$$ 此时,消费者可以观测到公司付出的保鲜努力,当
$e {\text{<}} e^*$ 时,$V_1 {\text{<}}V_1^*$ 。因此在完全信息情况下,公司投入的保鲜努力为${e^*}$ ,达到帕累托最优。2.2 不完全信息下CSA合作模型
在不完全信息情况下,生鲜农产品公司投入的保鲜努力是私人信息,投资型消费者无法观测。虽然消费者不能观测到公司的努力程度,但通过与公司之间的契约,能够实现自身效用的最大化。
对消费者效用函数
${U_1}(\beta ,e)$ 和生鲜农产品公司效用函数${U_2}(\beta ,e)$ 分别求偏导,得到$$\begin{split} &\qquad\frac{{\partial {U_1}(\beta ,e)}}{{\partial \beta }} = 2\lambda (1 \;-\; \beta ){(p \;- w)^2}{\sigma ^2} \;-\; (p \;-\; w)(a -bp) \times\\& \left(\frac{{\theta _0^T - 1}}{{\ln {\theta _0}}} + {k_1}eT\right); \end{split} $$ $$\qquad\frac{{\partial {U_2}(\beta ,e)}}{{\partial e}} = \beta (p - w)(a - bp){k_1}T - {k_2}e{\textit{。}} $$ 根据一阶偏导数
$\dfrac{\partial {U}_{1}(\beta ,e)}{\partial \beta }=0,\;\dfrac{\partial {U}_{2}(\beta ,e)}{\partial e}=0$ ,联立求解即可得到公司的最优收益共享系数$\beta = \dfrac{{A{k_2}}}{{B(p - w)}}$ 和付出的最优保鲜努力$e = \dfrac{{(a - bp){k_1}TA}}{B}$ 。其中,$A = 2\lambda (p - w){\sigma ^2} - (a - bp) \left(\dfrac{{\theta _0^T - 1}}{{\ln {\theta _0}}}\right)$ ,$B = 2\lambda {\sigma ^2}{k_2} + (a - $ $bp{)^2}k_1^2{T^2} $ 。将$\;\beta $ 、$e $ 代入到消费者效用函数${U_1}(\beta ,e)$ 和生鲜农产品公司利润函数${U_2}(\beta ,e)$ 中,即可得投资型消费者和生鲜农产品公司的效用。2.3 完全信息和不完全信息模型比较
完全信息情况下,生鲜农产品公司投入的最优保鲜努力水平
${e^*} = \dfrac{{(p - w)(a - bp){k_1}T}}{{{k_2}}}$ ,最优共享系数${\;\beta ^{\rm{*}}}{\rm{ = 1}}$ ,消费者最优投资金额$V_1^{\rm{*}} = {V_2} - (p - w)(a - bp) \times$ $\left[{\left(\dfrac{{\theta _0^T - 1}}{{{\rm{ln}}{\theta _0}}}\right) - \dfrac{{k_1^2{T^2}(p - w)(a - bp)}}{{2{k_2}}}} \right]$ ;不完全信息下,公司投入的最优保鲜努力水平$e = \dfrac{{(a - bp){k_1}TA}}{B} {\text{<}} {e^*}$ ,最优共享系数$\;\beta = \dfrac{{A{k_2}}}{{B(p - w)}} {\text{<}} {\beta ^*}$ ,消费者最优投资金额${V}_{1}={V}_{2}-\dfrac{A{k}_{2}(a-bp)}{B}\left[\left(\dfrac{{\theta }_{0}^{T}-1}{\mathrm{ln}{\theta }_{0}}\right)-\dfrac{A{k}_{2}(a-bp){k}_{1}^{2}{T}^{2}}{2B}\right]$ 。生鲜农产品公司在不完全信息情况下节约的保鲜成本为
$$ \qquad\Delta {C}_{1}=\frac{{(p-w)}^{2}{(a-bp)}^{2}{k}_{1}{}^{2}{T}^{2}(1-{\beta }^{2})}{2{k}_{2}}{\textit{。}} $$ 增加的收益为
$$\qquad\Delta {\pi }_{2}=\frac{{(p-w)}^{2}{(a-bp)}^{2}{k}_{1}{}^{2}{T}^{2}(1+3{\beta }^{2}-4\beta )}{2{k}_{2}}{\textit{。}}$$ 消费者由于信息不完全而损失的收益为
$$ \begin{split} &\qquad\Delta {\pi _1} = \frac{{(p - w)(a - bp){k_1}^2{T^2} + {k_2}\left(\dfrac{{\theta _0^T - 1}}{{{\rm{ln}}{\theta _0}}}\right)}}{{{k_2}B}}(1 - \beta )(p - w) \times\\&(a - bp{)^3}{k_1}^2{T^2}{\textit{。}} \end{split} $$ 通过计算得到完全信息和不完全信息情况下生鲜农产品公司的最优保鲜努力水平和收益共享系数,则公司对于保鲜努力的最优决策和投资型消费者对于收益共享系数的最优决策如下。
命题1 在完全信息情况下,当
$(p - w) (a - bp) \times$ ${k_1}T {\text{<}} {k_2} $ 时,公司的付出的最优保鲜努力为${e^{\rm{*}}} = \dfrac{{(p - w)(a - bp){k_1}T}}{{{k_2}}}$ ;当$(p - w)(a - bp){k_1}T {\text{>}} {k_2}$ 时,公司的最优保鲜努力${e^{\rm{*}}} = 1$ 。在不完全信息情况下,当$\dfrac{A}{B} \leqslant 0$ 时,保鲜努力水平$e$ $ = 0$ ,此时公司不投入保鲜努力;当$0 {\text{<}} \dfrac{A}{B} {\text{<}} \dfrac{1}{{(a - bp){k_1}T}}$ 时,公司的最优保鲜努力为$e = \dfrac{{(a - bp){k_1}TA}}{B}$ ;当$\dfrac{A}{B} \geqslant \dfrac{1}{{(a - bp){k_1}T}}$ 时,公司的保鲜努力为1。命题2 在完全信息情况下,
$\;{\beta ^{\rm{*}}}{\rm{ = }}1$ 。在不完全信息情况下,当$\dfrac{A}{B} \leqslant 0$ 时,生鲜农产品公司的收益共享系数$\;\beta {\rm{ = }}0$ ,即销售所得都为消费者所拥有,公司没有销售收益;当$0 {\text{<}} \dfrac{A}{B} {\text{<}} \dfrac{{p - w}}{{{k_2}}}$ 时,公司可得到的最优收益共享系数$\;\beta = \dfrac{{A{k_2}}}{{B(p - w)}}$ ;当$\dfrac{A}{B} \geqslant \dfrac{{p - w}}{{{k_2}}}$ 时,$\;\beta $ =1,此时全部销售收益归公司所有。命题1和2确定了生鲜农产品公司付出的最优保鲜努力水平和其最优收益共享系数的取值范围。在完全信息情况下,公司的保鲜决策与消费者对价格的敏感系数
$b$ 有关,当$b$ 发生变化,$e$ 也会随之变化。在不完全信息情况下,$A$ 和$B$ 中含有投资型消费者的风险规避系数$\lambda $ 和其对价格的敏感系数$b$ ,则当消费者对生鲜农产品价格的敏感度和对风险的态度发生转变时,$e$ 和$b$ 会随之变化。命题3 在不完全信息情况下,收益共享系数
$\beta $ 受到各个因素的影响,是关于消费者风险规避度$\lambda $ 的单调增函数;收益共享系数$\beta $ 与生鲜农产品价格有关,当$3bp - \dfrac{{2\lambda {\sigma ^2}{k_2}}}{{(a - bp)k_1^2{T^2}}} {\text{<}} a + 2bw$ 时,$\;\beta $ 是关于价格的单调增函数,当$3bp - \dfrac{{2\lambda {\sigma ^2}{k_2}}}{{(a - bp)k_1^2{T^2}}} {\text{>}} a + 2bw$ 时,$\beta $ 是关于价格的单调减函数。证明 对
$\;\beta $ 关于$\lambda $ 求导,得到$\dfrac{{\partial \beta }}{{\partial \lambda }} \geqslant 0$ 。因此,$\beta $ 是关于$\lambda $ 的单调增函数。也就是说,在不完全信息情况下,投资型消费者越是厌恶风险,生鲜农产品公司承担的风险越大,消费者制定的合作机制作用越强,设计合同时就要给予生鲜农产品公司更高的收益共享系数$\;\beta $ 。对收益共享系数
$\beta $ 关于生鲜农产品价格$p$ 求导,得到$\dfrac{{\partial \beta }}{{\partial p}}{\rm{ = }}\dfrac{{2\lambda {\sigma ^2}{k_2} + b}}{{2\lambda {\sigma ^2}{k_2} + (a - bp)k_1^2{T^2}(a - 3bp + 2bw)}}$ ,当$3bp - \dfrac{{2\lambda {\sigma ^2}{k_2}}}{{(a - bp)k_1^2{T^2}}} {\text{<}} a + 2bw$ 时,$\dfrac{{\partial \beta }}{{\partial p}} {\text{>}} 0$ ,$\;\beta $ 关于$p$ 单调递增;当$3bp - \dfrac{{2\lambda {\sigma ^2}{k_2}}}{{(a - bp)k_1^2{T^2}}} {\text{>}} a + 2bw$ 时,$\dfrac{{\partial \beta }}{{\partial p}} {\text{<}} 0$ ,$\;\beta $ 关于$p$ 单调递减。因此投资型消费者在决策$\;\beta $ 时,应充分考虑不同的情况。命题4 公司投入的保鲜努力
$e$ 与价格有关,保鲜努力随着价格的增加先增后减,且有最大值;在不完全信息下,$e$ 还受$\lambda $ 的影响,是关于$\lambda $ 的单调增函数。对
${e^{\rm{*}}}$ 关于$p$ 求导,令$\dfrac{{\partial {e^{\rm{*}}}}}{{\partial p}} = 0$ ,解得${p^{\rm{*}}}{\rm{ = }}\dfrac{{a + wb}}{{2b}}$ 。在完全信息情况下,当$p{\rm{ = }}\dfrac{{a + wb}}{{2b}}$ 时,$e$ 达到最大值;在不完全信息情况下,对$e$ 关于$p$ 求导,令$\dfrac{{\partial e}}{{\partial p}} = 0$ ,解得$p{\rm{ = }}\dfrac{{B\left[b\left(\dfrac{{\theta _0^T - 1}}{{\ln {\theta _0}}}\right) - \lambda {\sigma ^2}(a - bw)\right] - k_1^2{T^2}bA}}{{B\left[\left(\dfrac{{\theta _0^T - 1}}{{\ln {\theta _0}}}\right) - \lambda {\sigma ^2}2b\right] - k_1^2{T^2}A}}$ ,此时$e$ 达到最大值;对$e$ 关于$\lambda $ 求导,得到$\dfrac{{\partial e}}{{\partial \lambda }} \geqslant 0$ ,因此,$e$ 随着$\lambda $ 的增加而增加。即当消费者的风险规避度越大,合作契约的激励作用越强,公司为了获取更多的利润会加大保鲜努力的投入。3. 数值仿真
利用数值算例来验证模型探讨得到的相关结论,并讨论投资型消费者风险规避度对生鲜农产品公司决策的影响。参数的赋值为
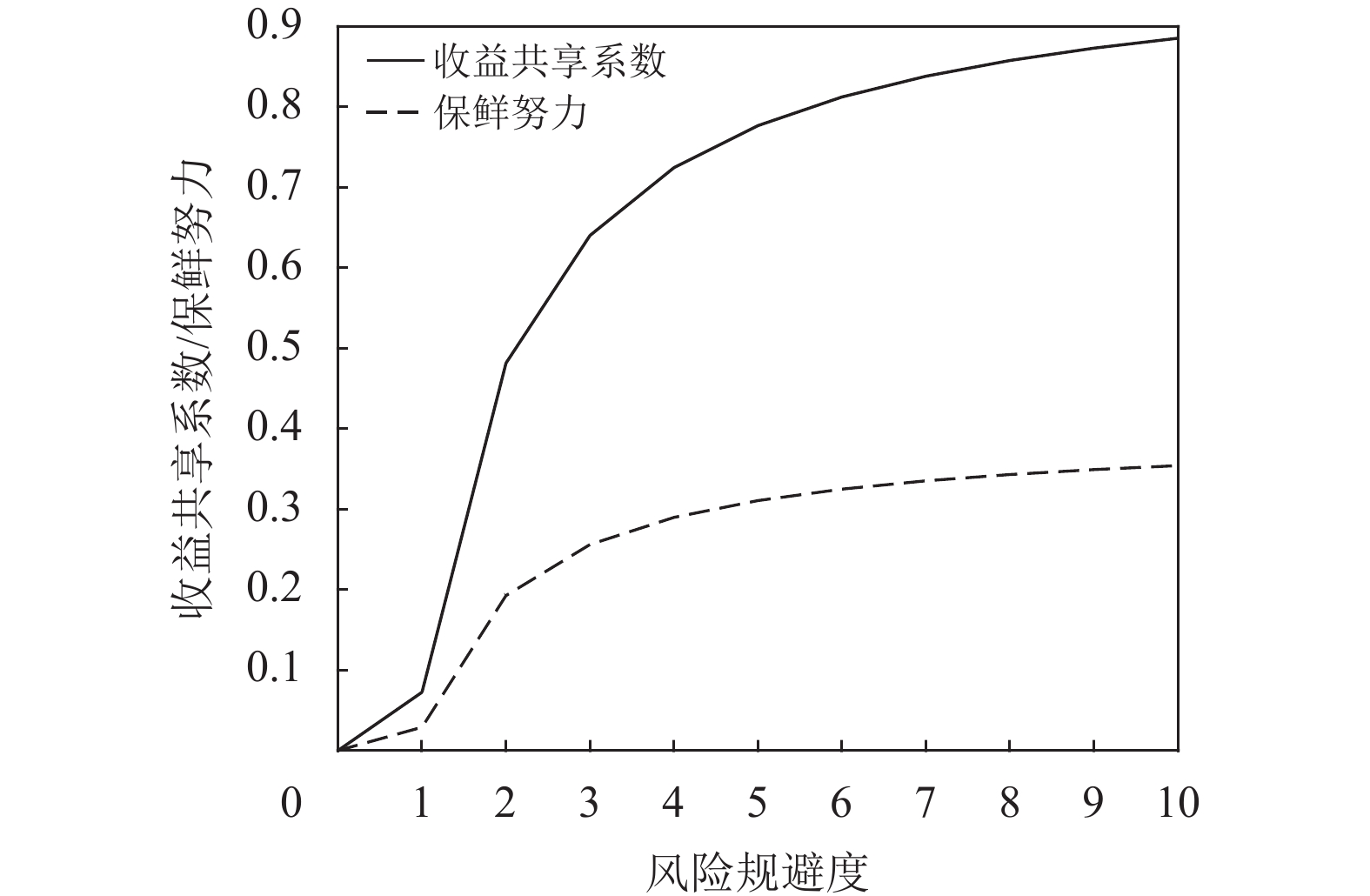
$a$ =100,$b$ =10,${k_1}$ =0.2,${k_2}$ =300,$w$ =5,$p$ =8,$T$ =10,${\theta _0}$ =0.7,${V_1}$ =50,${V_2}$ =30。将以上参数值代入相关表达式中,利用Matlab进行运算,得到图1~5。图1是不完全信息情况下投资型消费者的风险规避度对生鲜农产品公司收益共享系数和保鲜努力的影响。随着消费者风险规避度的增加,公司的收益共享系数和投入的保鲜努力都增加,但增加速率变得迟缓。即随着风险规避度的增加,收益共享系数和保鲜努力对其敏感度逐渐减弱。当风险规避度为0时,也就是消费者是风险中性时,收益共享系数和保鲜努力都为0,意味着公司此时得不到销售收益也不会付出保鲜努力。风险规避度越大表示消费者越厌恶风险,不愿承担风险,为了可以吃到质量更好的生鲜农产品,消费者愿意提高收益共享系数,用于加强公司在保鲜方面的投入。收益共享系数越大意味着生鲜农产品公司收益越多,此时公司更愿意投入保鲜努力提高生鲜农产品的质量,来获取更高的利润。
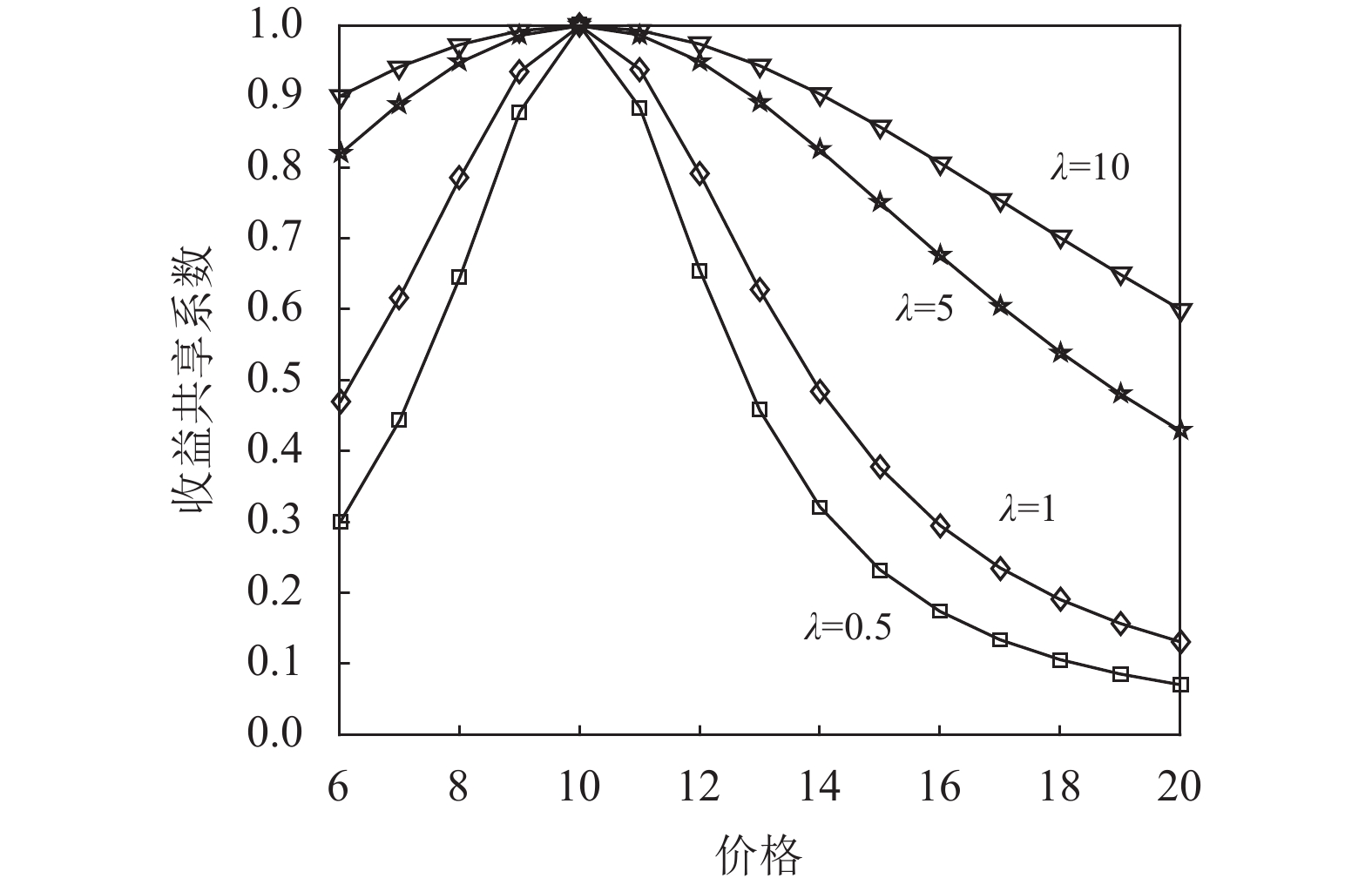
图2是不完全信息情况下生鲜农产品的价格对收益共享系数的影响图。从图中可以看出,随着价格的增加,收益共享系数先增加后减少,且存在最优的价格使得收益共享系数最高。风险规避度越高,收益共享系数越大。因此消费者需要预测农产品的价格,考虑不同的情形,进而决策生鲜农产品公司的收益共享系数。
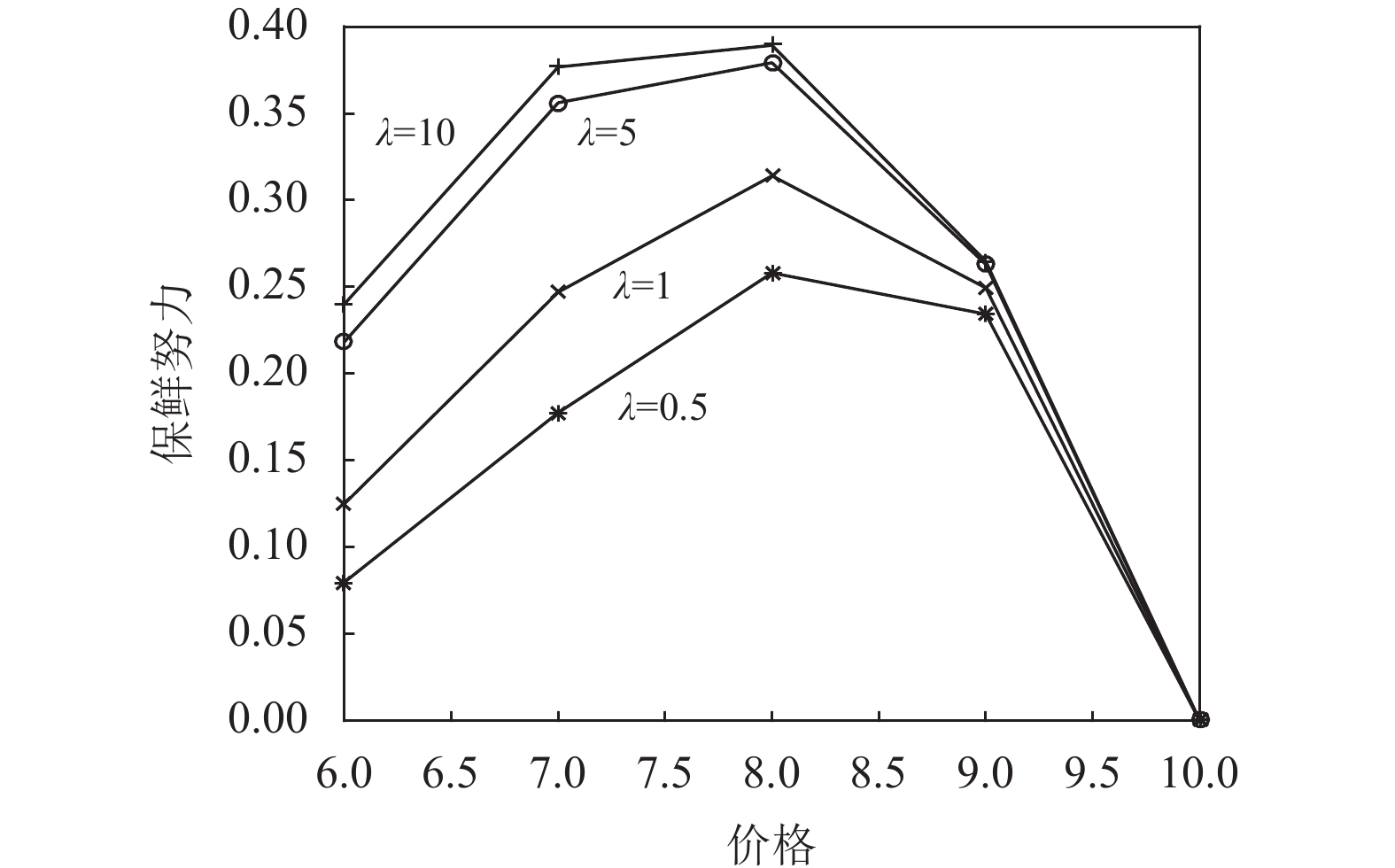
图3是不完全信息情况下生鲜农产品的价格对公司投入保鲜努力的影响。随着价格的增加,保鲜努力先增加后减少,存在最优的价格使得保鲜努力最大。投资型消费者的风险规避度越高,公司投入的保鲜努力越大。因此公司在投入保鲜努力时,不仅需要考虑消费者的风险规避度,还要预测农产品的市场价格,考虑不同的情况,作出最优的决策。
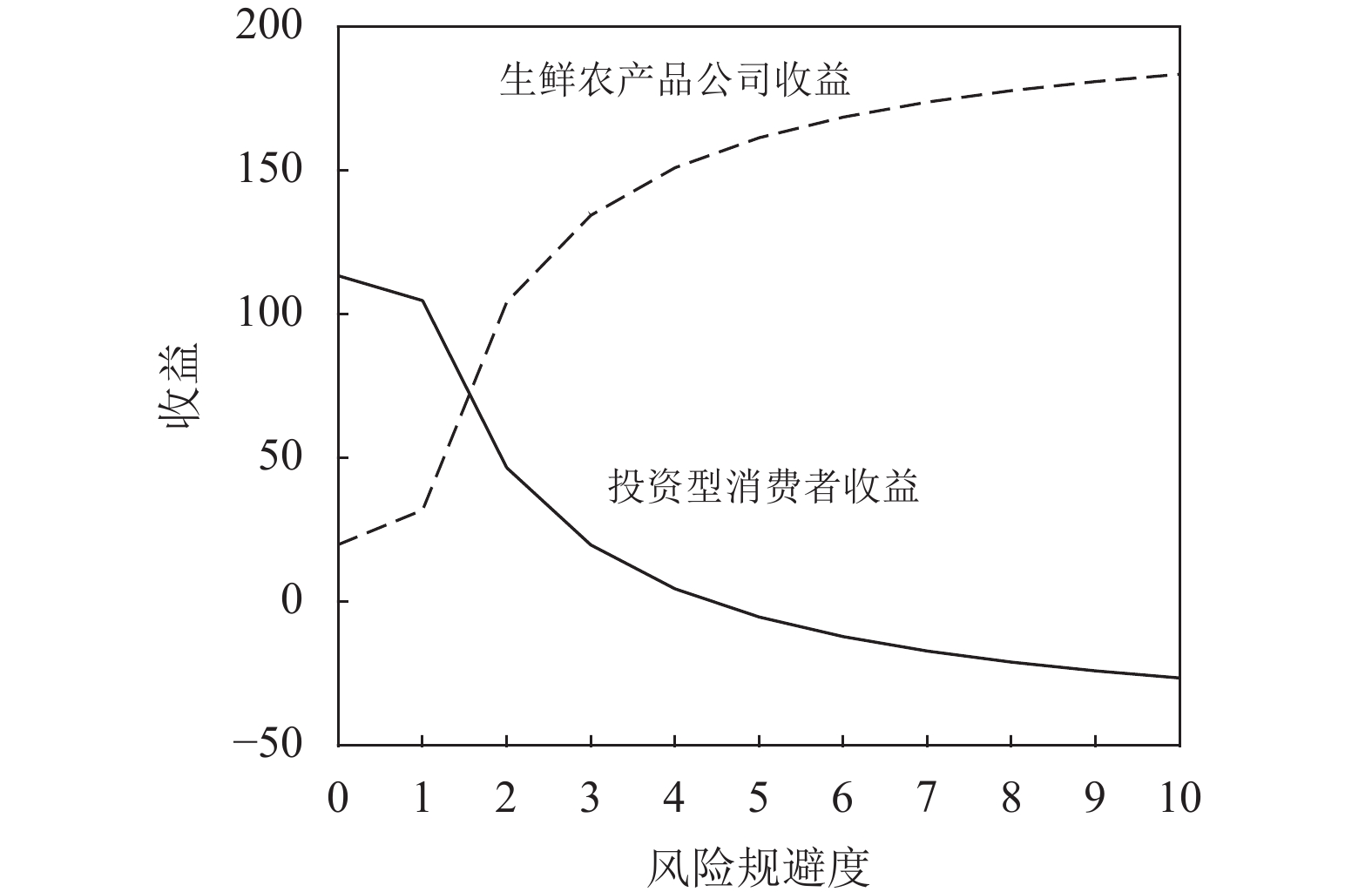
图4是不完全信息情况下投资型消费者的风险规避度对收益的影响。从图4可以看出,消费者的收益随着其风险规避度的增加而减少,而生鲜农产品公司的收益则随着消费者风险规避度的增加而增加。结合图1,风险规避度的增加使得收益共享系数增加,因此公司的收益也随之增加,而消费者的收益共享比例越来越低,因此消费者的收益减少。随着消费者风险规避度的增加,公司为了得到更多收益,会加大保鲜努力的投入。CSA中消费者对公司的投资,让公司在投入保鲜努力的同时可以有更高的收益。虽然公司加大了保鲜投入,但消费者愿意给予公司更多支持,用于提高生鲜农产品的质量,保证公司提供新鲜农产品。而对于消费者来说,虽然进行投资使得消费者收益降低,但可以食用到新鲜放心的农产品,其效用是增加的。
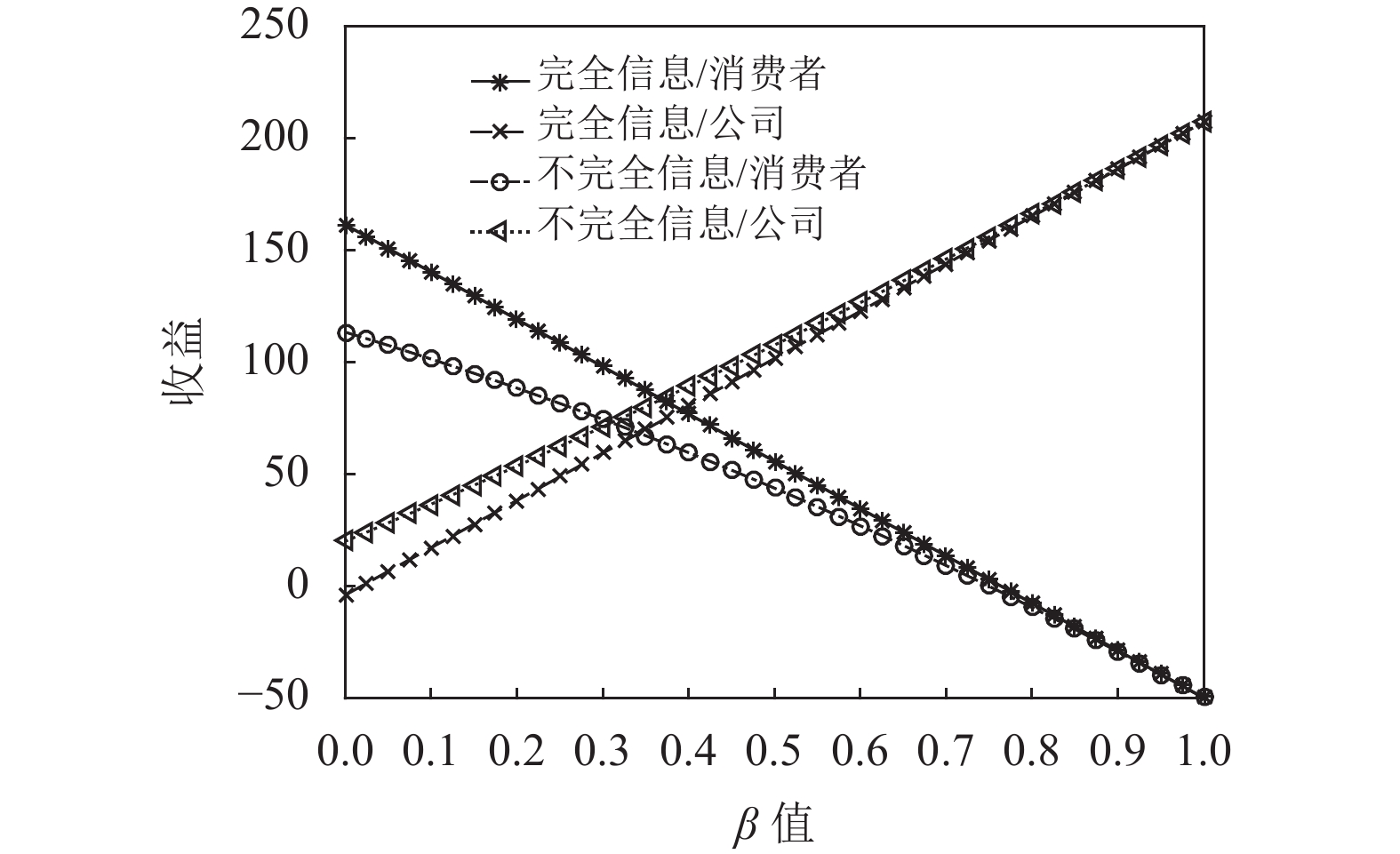
图5是完全信息和不完全信息情况下,投资型消费者和生鲜农产品公司的收益图。可以看出,不管在何种情况下,消费者的收益是随着
$\;\beta $ 的增加递减,而公司的收益随着$\;\beta $ 的增加递增。完全信息下消费者的收益高于不完全信息情况下,而不完全信息情况下公司的收益高于完全信息下。在完全信息情况下,消费者可以观测到公司的保鲜努力信息,公司会付出最优的保鲜努力,来达到最优的契约,因此增加了保鲜成本,导致公司在完全信息下的收益较低;而在不完全信息下,生鲜农产品公司隐藏自己的保鲜努力信息,消费者在决策时会进行预测,增加了风险成本,导致消费者在不完全信息下的收益较低。4. 结论
本文研究了由生鲜农产品公司推动的CSA体系在完全和不完全信息情况下,投资型消费者的风险规避度对公司收益和决策的影响。生鲜农产品的需求受其价格和新鲜度的影响,其中新鲜度对需求的影响是正向的,即新鲜度越高生鲜农产品的需求越大。因此投入保鲜努力能够使得生鲜农产品在销售时有较高的新鲜度,吸引消费者购买。CSA体系中,消费者和生产者建立了良好的信任,消费者能够理解生产者的付出,愿意承担生产者的风险,因此消费者更愿意给生鲜农产品公司投资,用于帮助农户生产以及公司运营。本文从投资型消费者的效用出发,发现在完全信息情况下,投资型消费者和生鲜农产品公司签订合作契约,存在帕累托最优结果;在不完全信息情况下,消费者的风险规避度越高生鲜农产品公司的收益越高,公司也会投入更多的保鲜努力,保障生鲜农产品的新鲜度以此来增加自身的收益。随着风险规避度的增加投资型消费者收益递减,但可以食用到新鲜放心的农产品反而使得消费者更愿意付出,因此生鲜农产品公司的收益共享系数与消费者的风险规避度正相关。生鲜农产品公司在面对消费者时,可根据消费者的特征来进行保鲜和收益共享系数的决策。这些研究结果,对CSA模式下的农产品公司发展具有一定的理论指导和现实意义。
本文考虑了消费者的风险规避度,但没有考虑农产品公司的风险态度,公司不同的风险态度会影响公司的决策。本文加入了新鲜度,但没有考虑生鲜农产品的新鲜度对其价格的影响,不同新鲜度的生鲜农产品价格必定有一定的差距。之后在这些方面还可以进行更多的研究。
-
[1] LAMB G. Community supported agriculture can it become the basis for a new associative economy[J]. The Threefold Review, 1994, 196(11): 8-15.
[2] 文亮, 丁晓露. 社区支持农业(CSA)在中国的发展现状及对策[J]. 上海农村经济, 2014(6): 35-37. DOI: 10.3969/j.issn.1671-6485.2014.06.009 [3] 朱明. 社区支持农业的研究进展[J]. 世界地理研究, 2018, 27(2): 106-117. DOI: 10.3969/j.issn.1004-9479.2018.02.011 ZHU Ming. Research progress of community supported agriculture[J]. World Regional Studies, 2018, 27(2): 106-117. DOI: 10.3969/j.issn.1004-9479.2018.02.011
[4] 张羽. 中国社区支持农业模式的研究[D]. 北京: 北京交通大学, 2015. ZHANG Yu. Research on community supported agriculture in China[D]. BEIJING: Beijing Jiaotong University, 2015.
[5] 陈卫平. 社区支持农业劳动份额的消费者价值认知结构: 方法目的链的应用[J]. 农业技术经济, 2012(9): 84-95. [6] 董欢, 郑晓冬, 方向明. 社区支持农业的发展: 理论基础与国际经验[J]. 中国农村经济, 2017(1): 84-94, 98. DONG Huan, ZHENG Xiaodong, FANG Xiangming. The development of community supported agriculture: theoretical foundation and international experience[J]. China Rural Economy, 2017(1): 84-94, 98.
[7] 杨波. 我国城市居民加入“社区支持农业”的动机与影响因素的实证研究——基于中西方国家对比的视角[J]. 中国农村观察, 2014(2): 73-83. YANG Bo. Emprical research on the motivations and influencing factors of Chinese urban residents joining CSA: from the aspect of comparison with western country consumers[J]. China Rural Survey, 2014(2): 73-83.
[8] 林文声, 钟倩琳, 王志刚. 社区支持农业的消费者忠诚研究—以珠海市绿手指份额农园为例[J]. 消费经济, 2016, 32(1): 57-62. [9] 石嫣, 程存旺. 生态型都市农业发展与城市中等收入群体兴起相关性分析[J]. 贵州社会科学, 2011(2): 55-60. DOI: 10.3969/j.issn.1002-6924.2011.02.010 [10] 陈卫平. 社区支持农业: 理论与实践[M]. 北京: 经济科学出版社, 2014: 34-44. [11] 戴君玲. 台湾社群支持性农业的发展与运作: 岛屿社群生机农场的个案研究[D]. 台北: 台湾大学, 2010. [12] 温铁军. CSA模式是建设生态型农业的有效途径之一[J]. 中国合作经济, 2009(10): 44. DOI: 10.3969/j.issn.1006-6063.2009.10.024 [13] 刘丽伟. 我国发展社区支持农业的多功能价值及路径选择[J]. 学术交流, 2012(9): 100-103. DOI: 10.3969/j.issn.1000-8284.2012.09.023 [14] 付会洋, 叶敬忠. 兴起与围困: 社区支持农业的本土化发展[J]. 中国农村经济, 2015(6): 23-32. [15] 王磊, 但斌. 考虑消费者效用的生鲜农产品供应链保鲜激励机制研究[J]. 管理工程学报, 2015, 29(1): 200-206. DOI: 10.3969/j.issn.1004-6062.2015.01.026 WANG Lei, DAN Bin. The incentive mechanism for preservation in fresh agricultural supply chain considering consumer utility[J]. Journal of Industrial Engineering and Engineering Management, 2015, 29(1): 200-206. DOI: 10.3969/j.issn.1004-6062.2015.01.026
[16] 杨果, 陈瑶. 新型农业经营主体参与低碳农业发展的激励机制设计[J]. 中国人口资源与环境, 2016(6): 94-99. YANG Guo, CHEN Yao. Design of the incentive mechanism that new agricultural operators participate in low-carbon agricultural development[J]. China Population, Resources and Environment, 2016(6): 94-99.
[17] 郑琪, 范体军. 考虑风险偏好的生鲜农产品供应链激励契约设计[J]. 管理工程学报, 2018, 32(2): 171-178. ZHENG Qi, FAN Tijun. Design of incentive contract for fresh agricultural products supply chain considering risk preference[J]. Jonrnal of Industrial Engineering and Engineering Management, 2018, 32(2): 171-178.
[18] SHENG Xitai, ZHANG Zhenji, GAO Honghu, et al. Optimization of incentive contracts leading enterprises to participate in low-carbon agricultural development[J]. Environmental Engineering and Management Journal, 2018(1): 237-244.
[19] 曲优, 关志民, 赵莹. 考虑生产商风险规避的农产品绿色投资策略演化研究[J]. 工业工程, 2019, 22(3): 65-76. DOI: 10.3969/j.issn.1007-7375.2019.03.009 QU You, GUAN Zhimin, ZHAO Ying. Green investment strategy selection and behavioral evolution of original agricultural products with risk-averse manufacturers[J]. Industrial Engineering Journal, 2019, 22(3): 65-76. DOI: 10.3969/j.issn.1007-7375.2019.03.009
[20] 江世英, 李随成, 王欢. 考虑风险规避的绿色供应链定价决策[J]. 系统工程, 2016, 34(3): 94-100. JIANG Shiying, LI Suicheng, WANG Huan. Pricing decision of green supply chain considerding risk aversion[J]. Systems Engineering, 2016, 34(3): 94-100.
-
期刊类型引用(3)
1. 杨扬,罗仲禹. 考虑消费者双重行为的农产品绿色供应链数字化策略. 管理工程师. 2024(03): 16-24 .  百度学术
百度学术
2. 朱盼盼,高甜村,张颖,邓俊锋,梅付春. 生鲜零售商应用区块链技术的意愿研究. 农业工程学报. 2024(20): 269-277 .  百度学术
百度学术
3. 肖湘雄,冶林扣. 社区支持农业中生产者与消费者共生关系演化逻辑. 安顺学院学报. 2022(06): 29-34 .  百度学术
百度学术
其他类型引用(5)



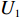
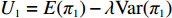
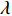

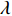
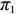
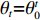
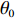
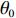
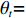
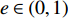
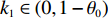
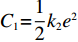
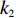
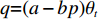
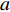
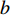
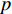
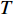

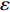
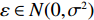
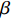
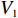
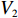
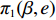
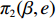
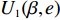
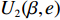
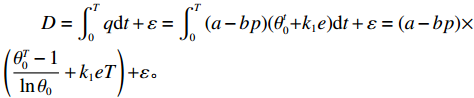
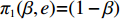
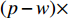
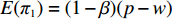
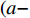
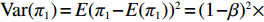
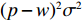
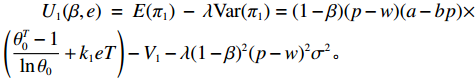
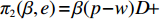
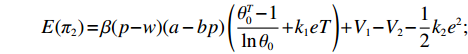
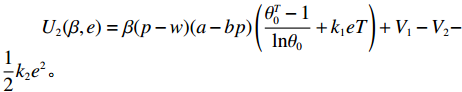
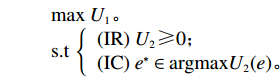
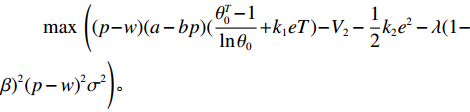
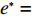
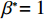

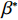
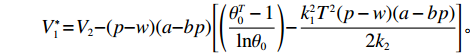
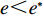
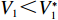
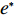
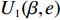
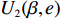
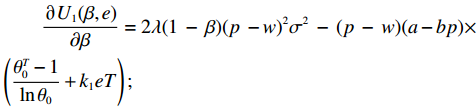
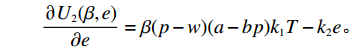
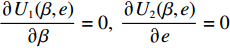

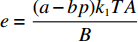
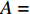
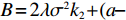
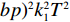
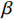
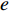
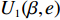
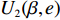
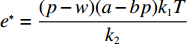
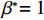
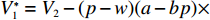
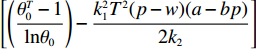
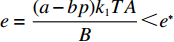
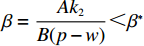

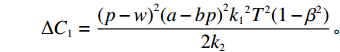
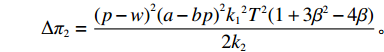
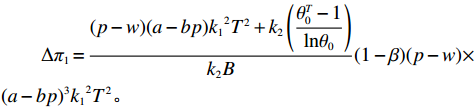
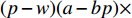
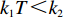
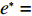
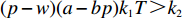
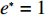
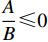
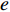
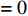
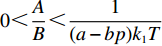
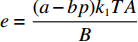
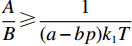

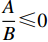
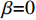
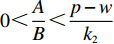
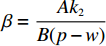
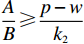

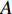
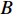
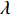
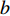
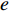
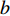
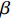
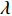
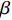
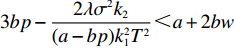
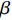
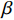
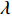
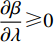
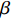
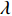
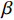
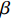
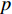
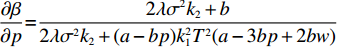
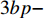
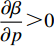
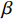
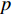
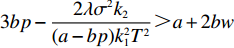
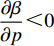
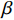
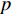
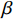

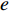
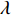
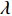
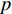
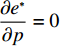
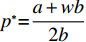
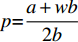
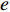

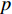
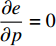
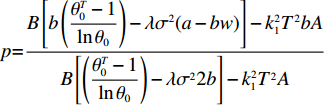
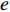
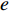
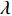
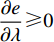
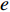
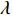
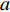
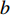
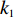
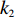
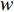
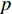
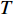
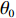
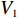
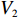
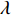
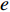
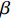
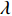
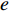
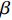
 下载:
下载: