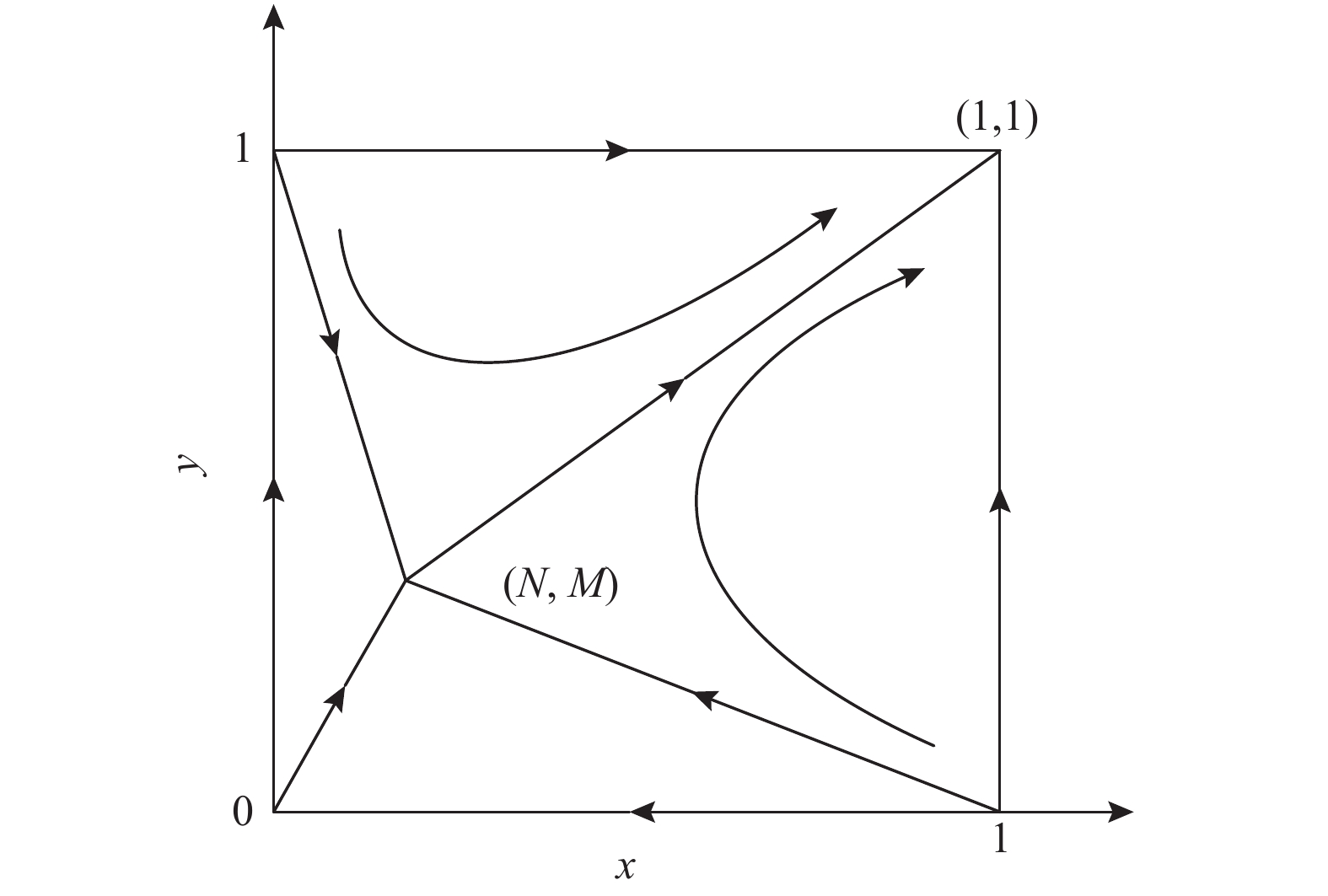
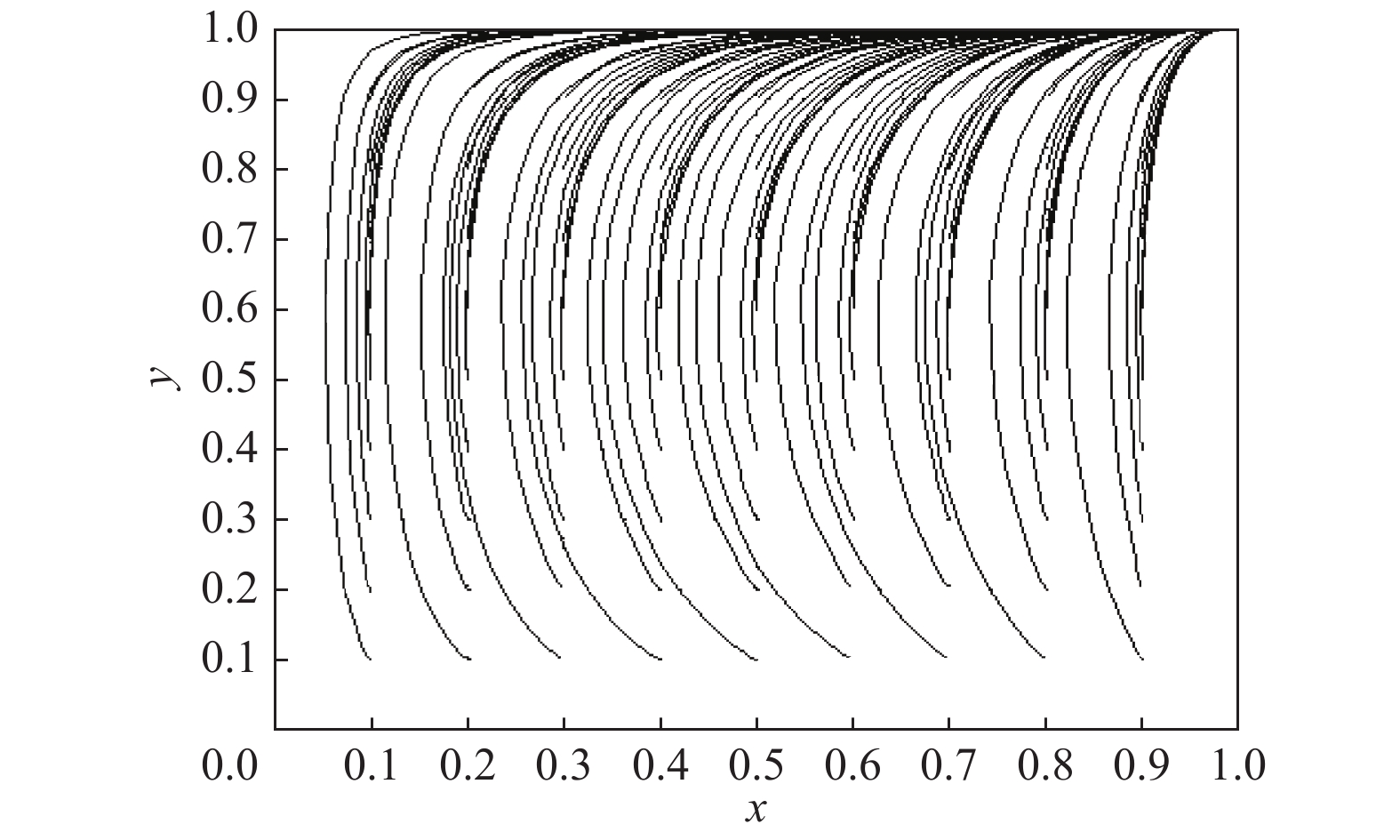
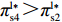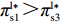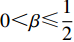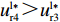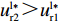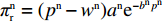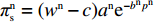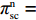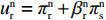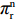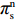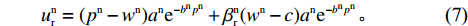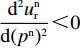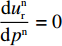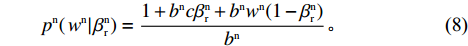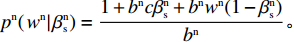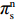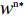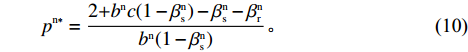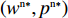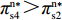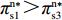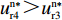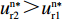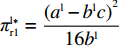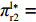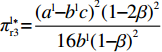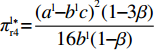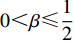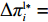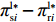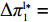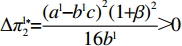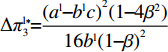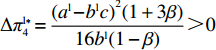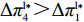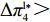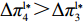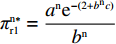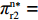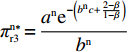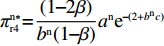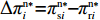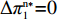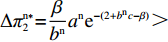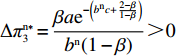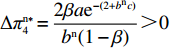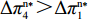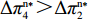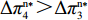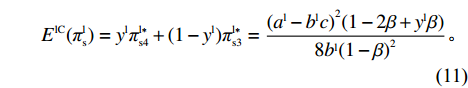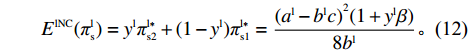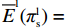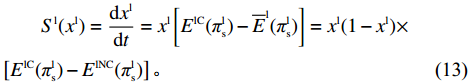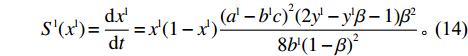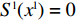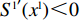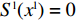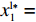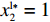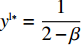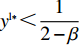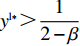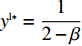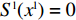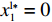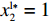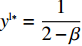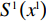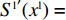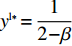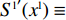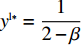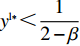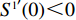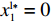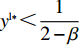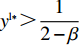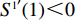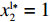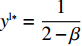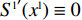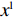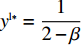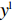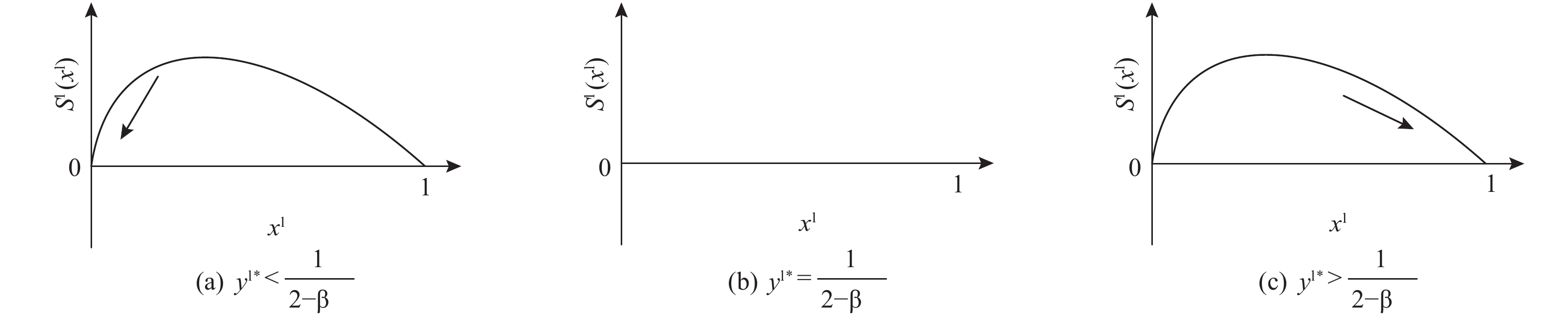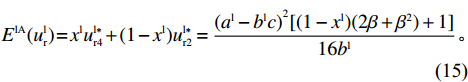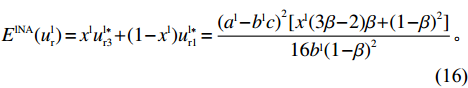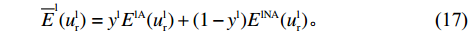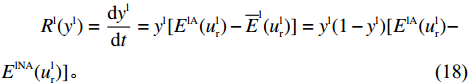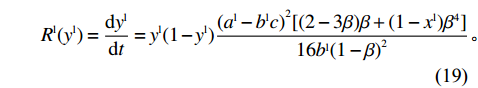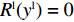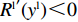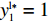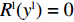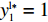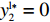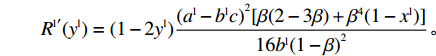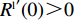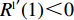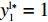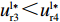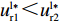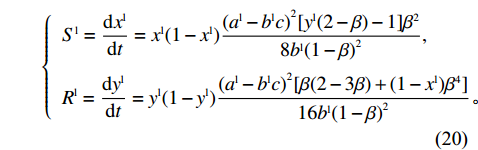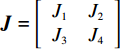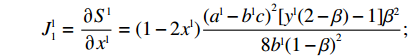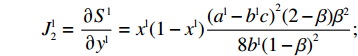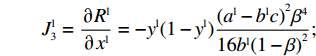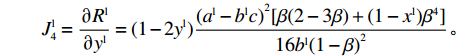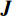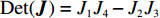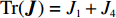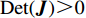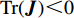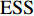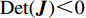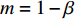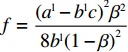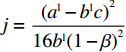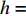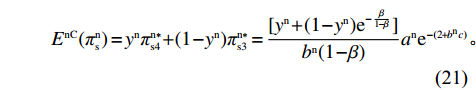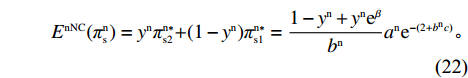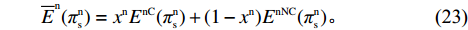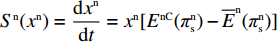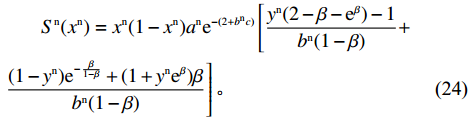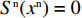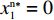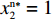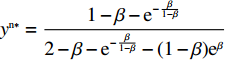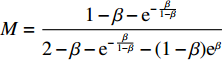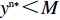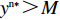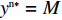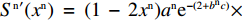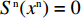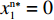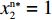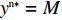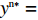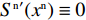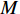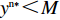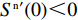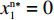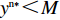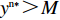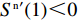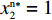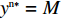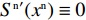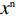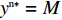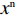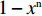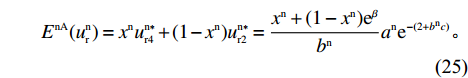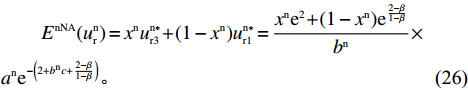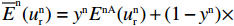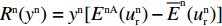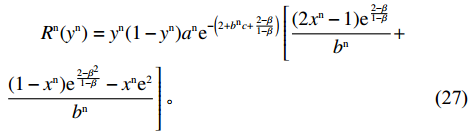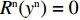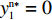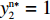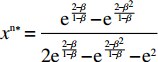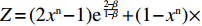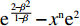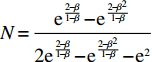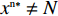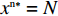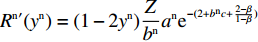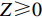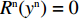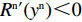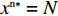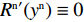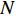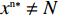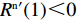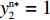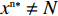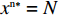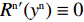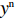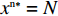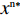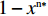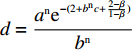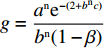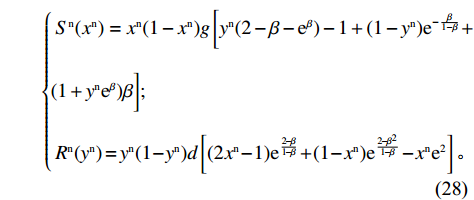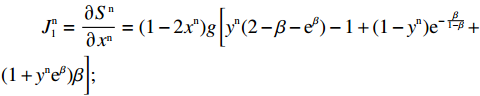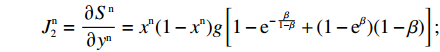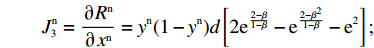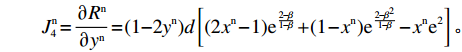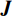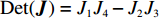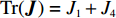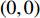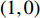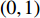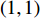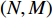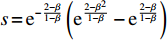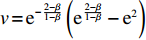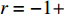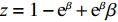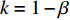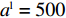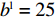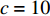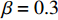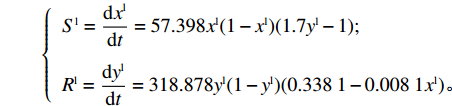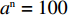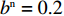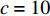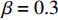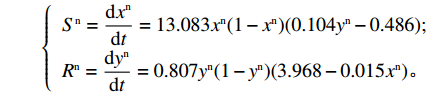A Research on Dynamic Evolution of Altruism Preference in Supply Chain Based on Evolutionary Game
-
摘要:
考虑供应链成员利他偏好行为和动态演进特征,分别在线性需求和非线性需求下建立相应的供应链决策模型。首先在短期内通过计算博弈支付矩阵对零供双方的均衡策略进行分析,其次在长期内运用演化博弈理论对零供双方进行单独演化分析、交互演化分析,最后将2种需求条件下供应链成员均衡策略进行比较,进而研究零售商利他偏好对供应链长期决策的影响。研究结果表明,短期内,供应商均衡策略依赖于零售商策略,而零售商均衡策略不受供应商影响且总是采取“偏好利他”策略;长期内,2种需求条件下零供博弈的均衡策略均为供应商采取“激励”策略、零售商采取“偏好利他”策略。此外,零售商利他偏好能提高供应商利润并使零售商实现效用最大化,进一步促进双方合作。
Abstract:Considering the altruism preference of supply chain members and the dynamic evolution of supply chain, the corresponding decision models under linear demand and nonlinear demand are established. Firstly, the equilibrium strategies of supplier-retailer game are analyzed in the short term. Then, the evolutionary game theory is used to analyze independent evolution and interactive evolution of supplier-retailer game in the long term. Finally, the supply chain members' equilibrium strategies are compared under two demand conditions and the influence of retailers' altruism preference on the members' strategies studied. The results show that the supplier's equilibrium strategy relies on the retailer's strategy in the short term, but the retailer's equilibrium strategy is not affected by the supplier's. In the short term, the retailer always chooses altruism strategy. In the long term, the supplier always chooses incentive strategy and the retailer always chooses altruism preference strategy. Furthermore, the retailer's altruism preference can maximize his utility and increase the supplier's profit. It is also found that the retailer's altruism preference can help to promote cooperation among members in supply chain.
-
随着数字化供应链时代的到来,如何更好地协调供应链利润分配,实现企业间互利共赢已成为各大企业新一轮关注的热点。诸多企业开始注重供应链成员间的相互合作并致力于提高供应链收益。同时,现实中有大量案例表明,供应链成员利他偏好会提高供应链成员利润并促进双方长期合作。例如,沃尔玛向中美洲的供应商提供支持,提高了供应商的银行贷款额度,并为农民提供农业可持续实践等技术培训,这不仅提高了供应商收益还提升了产品质量[1]。山东寿光大型连锁超市与农村合作社建立深度合作关系,超市免费对农产品进行运输、包装,合作社也主动派出专业生产人员帮助超市进行销售,双方达到互利共赢[2]。由此可见,将供应链成员利他偏好引入供应链进行研究对供应链成员的合作发展具有重要意义。
近年来,已有相关学者将利他偏好引入供应链进行研究,分析利他偏好行为在短期内对供应链成员决策的影响[3-6]。Ge等[7]构建演化决策模型分析供应网络中的利他属性,指出考虑利他属性对供应商和供应链系统是有利的。骆正清等[8]将利他偏好引入双渠道供应链,发现在Nash博弈中零售商利他程度越高,供应链利润越大。Shi等[9]发现双渠道供应链中零售商利他偏好程度越高,供应商就会制定更高的批发价格从而获取更多利润。在此基础上,骆正清等[10]再次对双渠道中供应链成员利他偏好进行研究并得出同样的结论。上述文献均在短期内对供应链成员利他偏好以及供应链成员决策进行研究,得出供应链成员利他偏好对供应链系统有利的结论。但以上文献均未考虑随着时间的推移,供应链成员是否会改变自己的定价决策,即忽略了供应链的动态演进特征。在现实中,由于企业判断力以及市场分析等差异,企业间的合作往往需要经历长期博弈和反复调整才能达到双方的稳定状态。例如,苹果公司在与第三方平台初期合作时,并未设置浮动奖励,但随着双方的长期博弈,他们决定在第三方平台进行废旧品回收时对其进行奖励,从而提高回收商积极性,同时增大自身利润[11]。因此,有必要考虑供应链的动态演进特征,研究利他偏好行为对供应链成员的影响,为供应链成员长期决策提供更科学的依据。
同时,出于自身利益考虑,现实中合作企业会隐藏自身私有信息,信息非对称现象在供应链管理中广泛存在,且会对供应链成员决策造成影响[12-17]。但现有研究利他偏好对供应链决策和协调性影响的文献大多基于信息对称条件。Bassi等[18]建立委托代理模型分析利他偏好对系统收益的影响,发现当供应链成员具有利他偏好时,供应链效率会显著提高。石岿然等[19]在信息对称情况下对双渠道供应链成员利他偏好进行研究,发现供应链成员更愿意选择具有利他偏好的企业进行合作。Xu等[20]运用共同竞争博弈理论研究线上线下零售商渠道之间的关系,证明利他偏好可以提高供应链效率。覃燕红等[21]将决策主体的利他偏好行为引入供应链决策模型进行研究,为决策主体选择合作伙伴类型提供了理论支持。以上研究均是在信息对称条件下研究利他偏好对供应链决策和协调性的影响,然而现实中信息非对称广泛存在于供应链中,是影响供应链协调的重要因素[22-26]。因此,在信息非对称下对供应链成员利他偏好进行研究更具有现实意义。
鉴于此,本文率先考虑供应链的动态演进特征,基于信息非对称条件,分别在线性市场需求和非线性市场需求下建立演化博弈模型,研究零售商利他偏好对零供决策的影响。首先,在短期内分析供应商和零售商的均衡策略。其次,在长期内对供应链成员进行单独演化分析和交互演化分析,对零供双方的长期均衡策略进行比较。最后,对供应链成员的演化稳定策略进行仿真分析,验证结论的准确性和有效性,为供应链良好运作提供更准确的理论依据。
1. 模型假设和符号说明
由供应商和零售商组成的二级供应链中,供应商和零售商是2个相互影响的种群,每个种群成员随机配对构成供应链并进行Stackelberg博弈。供应商和零售商根据自身支付不断学习、动态调整策略,直至达到均衡。供应商的策略选择为“激励”和“不激励”,零售商的策略选择为“偏好利他”和“不偏好利他”。供应商采取“激励”策略的概率为
x(0⩽x⩽1) ,采取“不激励”策略的概率为1−x ,即供应商群体里有比例x 的供应商在制定批发价格时考虑零售商利他偏好,而比例1−x 的供应商不考虑零售商利他偏好。同样,零售商采取“偏好利他”策略的概率为y(0⩽y⩽1) ,采取“不偏好利他”策略的概率为1−y ,即零售商群体有比例y 的零售商具有利他偏好,而比例1−y 的零售商不具有利他偏好。1) 供应商为领导者先根据自身单位生产成本
c 确定批发价格w ,零售商为跟随者根据市场需求确定零售价格p ,两者同时在博弈中不断调整策略以达到均衡。2) 假设双方在线性需求函数
ql=al−blpl 和非线性需求函数qn=ane−bnpn 下进行博弈。其中,al 、an 分别为线性需求和非线性需求下的市场规模,bl 、bn 分别为线性需求和非线性需求下产品价格对市场需求的参数。3) 由于零售商更靠近终端市场,更了解消费者需求,可以通过差异化营销扩大市场,于是零售商更希望通过自身利他偏好提高双方收益。因此,本文仅考虑零售商利他偏好,即零售商总是以包括自身利润和利他偏好正效用在内的总效用最大化为目标,而供应商始终以自身利润最大化为目标。
4) 零售商利他偏好真实值为
βr ,该值作为零售商的私有信息,供应商是无法观测到的。零供博弈时零售商表现出的利他偏好度为βs ,即供应商认为零售商利他偏好度为βs 。为方便计算,假定βr、βs∈{0,β} ,其中β 为某个特定正数。根据零售商是否真实反映自身利他偏好,分为信息对称和信息非对称。当信息对称时,零售商完全理性βr=βs=0 或具有利他偏好βr=βs=β ;当信息非对称时,零售商完全理性βr=0,βs=β 或具有利他偏好βr=β,βs=0 。同时,为了保证供应链所有成员利润为正,从而参与博弈,通过计算假设0⩽βr,βs⩽12 。5) 文中
π 表示利润,u 表示效用。下标“i ”表示零供交易的第i 种情形,下标“s”、“r”、“sc”分别表示供应商、零售商和供应链。上标“*”表示决策最优值,上标“l”、“n”分别表示线性和非线性需求下各函数取值。上标“C”、“NC”分别表示供应商采取“激励”策略、“不激励”策略的期望收益,上标“A”、“NA”分别表示零售商采取“偏好利他”策略、“不偏好利他”策略的期望收益。2. 博弈支付矩阵分析
2.1 线性需求函数下的博弈支付矩阵
线性需求下零售商、供应商、供应链的利润函数分别为
πlr=(pl−wl)(al−blpl) ;πls=(wl−c)(al−blpl) ;πlsc=(pl−c)(al−blpl) 。同参考文献[21],零售商利他偏好下的效用函数为
ulr=πlr+βlrπls。 (1) 式(1)中,第1项为零售商自身利润
πlr ;第2项是以供应商利润为参考点的零售商利他正效用βlrπls 。将
πlr 和πls 代入式(1),可得ulr=(pl−wl)(al−blpl)+βlr(wl−c)(al−blpl)。 (2) 易得
d2ulrd(pl)2=−2bl<0 。令dulrdpl=0 ,得零售商关于批发价格的真实反应函数pl(wl|βlr)=al+wlbl−(wl−c)blβlr2bl。 (3) 信息非对称下,供应商认为零售商反应函数为
pl(wl|βls)=al+wlbl−(wl−c)blβls2bl 。在此信念下,供应商决策的目标函数为
max (4) 由此得供应商的最优批发价格
\qquad {w^{{\rm{l}}*}} = \dfrac{{{a^{\rm l}} + {b^{\rm l}}c(1 - 2\beta _{\rm s}^{\rm l})}}{{2{b^{\rm l}}(1 - \beta _{\rm s}^{\rm l})}}{\text{。}} (5) 将
{w^{{\rm l}*}} 代入式(3)可得零售商实际最优定价为\qquad {p^{{\rm l}*}} = \dfrac{{3{a^{\rm l}} + {b^{\rm l}}c - 2({a^{\rm l}} + {b^{\rm l}}c)\beta _{\rm s}^{\rm l} - ({a^{\rm l}} - {b^{\rm l}}c)\beta _{\rm r}^{\rm l}}}{{4{b^{\rm l}}(1 - \beta _{\rm s}^{\rm l})}}{\text{。}} (6) 综上,在线性需求下,零售商和供应商博弈的子博弈精炼纳什均衡解为
({w^{{\rm l}*}},\;{p^{{\rm l}*}}) 。根据零售商和供应商的策略选择,结合上述变量假设与收益函数,得到短期内线性需求下博弈双方的支付矩阵,如表1所示。
表 1 线性需求下博弈双方的支付矩阵Table 1. The payoff matrix of both sides under linear demand供应商 零售商 偏好利他({y^{\rm l}}) 不偏好利他(1 - {y^{\rm l}}) 激励({x^{\rm l}}) \pi _{{\rm{s}}4}^{{\rm l}*} = \dfrac{ { { {({a^{\rm l} } - {b^{\rm l} }c)}^2} } }{ {8{b^{\rm l} }(1 - \beta )} } \pi _{{\rm s}3}^{{\rm l}*} = \dfrac{{{{({a^{\rm l}} - {b^{\rm l}}c)}^2}(1 - 2\beta )}}{{8{b^{\rm l}}{{(1 - \beta )}^2}}} u_{{\rm r}4}^{{\rm l}*} = \dfrac{{{{({a^{\rm l}} - {b^{\rm l}}c)}^2}}}{{16{b^{\rm l}}}} u_{{\rm r}3}^{{\rm l}*} = \dfrac{{{{({a^{\rm l}} - {b^{\rm l}}c)}^2}{{(1 - 2\beta )}^2}}}{{16{b^{\rm l}}{{(1 - \beta )}^2}}} 不激励(1 - {x^{\rm l}}) \pi _{{\rm s}2}^{{\rm l}*} = \dfrac{{{{({a^{\rm l}} - {b^{\rm l}}c)}^2}(1 + \beta )}}{{8{b^{\rm l}}}} \pi _{{\rm s}1}^{{\rm l}*} = \dfrac{{{{({a^{\rm l}} - {b^{\rm l}}c)}^2}}}{{8{b^{\rm l}}}} u_{{\rm r}2}^{{\rm l}*} = \dfrac{{{{({a^{\rm l}} - {b^{\rm l}}c)}^2}{{(1 + \beta )}^2}}}{{16{b^{\rm l}}}} u_{{\rm r}1}^{{\rm l}*} = \dfrac{{{{({a^{\rm l}} - {b^{\rm l}}c)}^2}}}{{16{b^{\rm l}}}} 命题1 线性需求函数下供应商短期均衡策略依赖于零售商策略,而零售商短期均衡策略不受供应商影响且始终为“偏好利他”。
证明 供应商在供应链中占据主导地位,自身具有先动优势,为了自身发展,会选择使自身利润最大的策略。由表1得
\pi _{{\rm s}4}^{{\rm l}*} {\text{>}} \pi _{{\rm s}2}^{{\rm l}*} ,\pi _{{\rm s}1}^{{\rm l}*} {\text{>}} \pi _{{\rm s}3}^{{\rm l}*} ,可见当零售商采取“偏好利他”策略时,供应商采取“激励”策略会获得更多的利润;而当零售商采取“不偏好利他”策略时,供应商采取“不激励”策略会获得更多的利润。根据零售商采取的不同策略,供应商采取相应的策略才能使自身利润达到最大,即供应商短期均衡策略并不是不变的,而是随零售商策略变化的。所以供应商短期均衡策略依赖于零售商策略。零售商总是以包括自身利润和利他偏好正效用在内的总效用最大化为目标,通过效用最大化选择自身策略。结合
0 {\text{<}} \beta \leqslant \dfrac{1}{2} 与表1得u_{{\rm r}4}^{{\rm l}*} {\text{>}} u_{{\rm r}3}^{{\rm l}*} ,u_{{\rm r}2}^{{\rm l}*} {\text{>}} u_{{\rm r}1}^{{\rm l}*} ,可见,无论供应商采取哪种策略,零售商采取“偏好利他”时的零售商效用总是大于采取“不偏好利他”的情形,即短期内,零售商“偏好利他”策略始终优于“不偏好利他”策略。此时,零售商利他偏好表现出利己现象,所以零售商短期均衡策略为“偏好利他”策略。2.2 非线性需求函数下的博弈支付矩阵
非线性需求下供应商、零售商、供应链利润函数分别为
\pi _{\rm r}^{\rm n} = ({p^{\rm n}} - {w^{\rm n}}){a^{\rm n}}{{\rm e}^{ - {b^{\rm n}}{p^{\rm n}}}} ;\pi _{\rm s}^{\rm n} = ({w^{\rm n}} - c){a^{\rm n}}{{\rm e}^{ - {b^{\rm n}}{p^{\rm n}}}} ;\pi _{{\rm sc}}^{\rm n} = ({p^{\rm n}} - c) {a^{\rm n}}{{\rm e}^{ - {b^{\rm n}}{p^{\rm n}}}} 。此时,零售商效用函数依然为
u_{\rm r}^{\rm n} = \pi _{\rm r}^{\rm n} + \beta _{\rm r}^{\rm n}\pi _{\rm s}^{\rm n} ,将\pi _{\rm r}^{\rm n} 和\pi _{\rm s}^{\rm n} 代入得\qquad u_{\rm r}^{\rm n} = ({p^{\rm n}} - {w^{\rm n}}){a^{\rm n}}{{\rm e}^{ - {b^{\rm n}}{p^{\rm n}}}} + \beta _{\rm r}^{\rm n}({w^{\rm n}} - c){a^{\rm n}}{{\rm e}^{ - {b^{\rm n}}{p^{\rm n}}}}{\text{。}} (7) 易得
\dfrac{{{{\rm d}^2}u_{\rm r}^{\rm n}}}{{{\rm d}{(p^{{\rm n}})^2}}} {\text{<}} 0 ,令\dfrac{{{\rm d}u_{\rm r}^{\rm n}}}{{{\rm d}{p^{\rm n}}}} = 0 ,得到零售商关于批发价格的真实反应函数\qquad {p^{\rm n}}(\left. {{w^{\rm n}}} \right|\beta _{\rm r}^{\rm n}) = \dfrac{{1 + {b^{\rm n}}c\beta _{\rm r}^{\rm n} + {b^{\rm n}}{w^{\rm n}}(1 - \beta _{\rm r}^{\rm n})}}{{{b^{\rm n}}}}{\text{。}} (8) 信息非对称下,供应商认为零售商的反应函数
{p^{\rm n}}(\left. {{w^{\rm n}}} \right|\beta _{\rm s}^{\rm n}) = \dfrac{{1 + {b^{\rm n}}c\beta _{\rm s}^{\rm n} + {b^{\rm n}}{w^{\rm n}}(1 - \beta _{\rm s}^{\rm n})}}{{{b^{\rm n}}}}{\text{。}} 将其代入\pi _{\rm s}^{\rm n} ,通过利润最大化得供应商最优批发价格\qquad {w^{{\rm n}*}} = \dfrac{{1{\rm{ + }}{b^{\rm n}}c(1 - \beta _{\rm s}^{\rm n})}}{{{b^{\rm n}}(1 - \beta _{\rm s}^{\rm n})}}{\text{。}} (9) 将
{w^{{\rm n}*}} 代入式(8),可得零售商实际最优定价\qquad {p^{{\rm n}*}} = \dfrac{{2{\rm{ + }}{b^{\rm n}}c(1 - \beta _{\rm s}^{\rm n}) - \beta _{\rm s}^{\rm n} - \beta _{\rm r}^{\rm n}}}{{{b^{\rm n}}(1 - \beta _{\rm s}^{\rm n})}}{\text{。}} (10) 综上,可以得到在非线性需求下,零供博弈的子博弈精炼纳什均衡解为
({w^{{\rm n}*}},{p^{{\rm n}*}}) 。根据零售商和供应商的策略选择,结合各阶段零供双方的收益函数,得到短期内非线性需求下博弈双方的支付矩阵,如表2所示。
表 2 非线性需求下博弈双方的支付矩阵Table 2. The payoff matrix of both sides under nonlinear demand供应商 零售商 偏好利他({y^{\rm n}}) 不偏好利他(1 - {y^{\rm n}}) 激励({x^{\rm n}}) \pi _{{\rm s}4}^{{\rm n}*} = \dfrac{{a^{\rm n}}{{\rm e}^{ - (2 + {b^{\rm n}}c)}}}{{{b^{\rm n}}(1 - \beta )}} \pi _{{\rm s}3}^{{\rm n}*} = \dfrac{{a^{\rm n}}{{\rm e}^{ - \left({b^{\rm n}}c + \frac{{2 - \beta }}{{1 - \beta }}\right)}}}{{{b^{\rm n}}(1 - \beta )}} {\rm{ }}u_{{\rm r}4}^{{\rm n}*} = \dfrac{{a^{\rm n}}{{\rm e}^{ - (2 + {b^{\rm n}}c)}}}{{{b^{\rm n}}}} {\rm{ }}u_{{\rm r}3}^{{\rm n}*} = \dfrac{{a^{\rm n}}{{\rm e}^{ - \left({b^{\rm n}}c + \frac{{2 - \beta }}{{1 - \beta }}\right)}}}{{{b^{\rm n}}}} 不激励(1 - {x^{\rm n}}) \pi _{{\rm s}2}^{{\rm n}*} = \dfrac{{a^{\rm n}}{{\rm e}^{ - (2 + {b^{\rm n}}c - \beta )}}}{{{b^{\rm n}}}} \pi _{{\rm s}1}^{{\rm n}*} = \dfrac{{a^{\rm n}}{{\rm e}^{ - (2 + {b^{\rm n}}c)}}}{{{b^{\rm n}}}} u_{{\rm r}2}^{{\rm n}*} = \dfrac{{a^{\rm n}}{{\rm e}^{ - (2 + {b^{\rm n}}c - \beta )}}}{{{b^{\rm n}}}} u_{{\rm r}1}^{{\rm n}*} = \dfrac{{a^{\rm n}}{{\rm e}^{ - (2 + {b^{\rm n}}c)}}}{{{b^{\rm n}}}} 命题2 短期内,非线性需求下供应商均衡策略依赖于零售商策略,而零售商均衡策略不受供应商影响且始终为“偏好利他”。
证明 由表2得
\pi _{{\rm s}4}^{{\rm n}*} {\text{>}} \pi _{{\rm s}2}^{{\rm n}*} ,\pi _{{\rm s}1}^{{\rm n}*} {\text{>}} \pi _{{\rm s}3}^{{\rm n}*} ,即当零售商采取不同的策略时,供应商的策略选择不同。现实中,大多数供应商作为供应链中的领导者,具有特有的地位优势,更容易通过制定不同的策略来获取更多利润。当零售商采取“偏好利他”策略时,供应商采取“激励”策略利润更大,而当零售商采取“不偏好利他”策略时,供应商采取“不激励”策略利润更大。可见,供应商短期均衡策略会受到零售商策略的影响,即供应商短期均衡策略是依赖于零售商策略的。零售商在供应链中处于被动地位,在零供双方博弈时会为供应商的利润考虑,主动表现出利他行为,从而促进零供双方的长期合作和发展。同时,由表2得
u_{{\rm r}4}^{{\rm n}*} {\text{>}} u_{{\rm r}3}^{{\rm n}*} ,u_{{\rm r}2}^{{\rm n}*} {\text{>}} u_{{\rm r}1}^{{\rm n}*} ,即无论供应商采取什么策略,零售商的利他偏好行为总能给自身带来更高的效用,所以零售商短期均衡策略为“偏好利他”策略。结论1 无论在线性需求下还是非线性需求下,供应商短期均衡策略均依赖于零售商策略,而零售商均衡策略不受供应商策略影响且始终为“偏好利他”。
证明 由命题1、命题2即可得证。
结论2 无论在线性需求下还是非线性需求下,零售商利润总是小于或等于供应商利润,且在供应商采取“激励”策略、零售商采取“偏好利他”策略时,零供之间利润差最大。
证明 经过计算,得
\pi _{{\rm r}1}^{{\rm l}*} = \dfrac{{{{({a^{\rm l}} - {b^{\rm l}}c)}^2}}}{{16{b^{\rm l}}}} ,\pi _{{\rm r}2}^{{\rm l}*} = \dfrac{{{{({a^{\rm l}} - {b^{\rm l}}c)}^2}(1 - {\beta ^2})}}{{16{b^{\rm l}}}} ,\pi _{{\rm r}3}^{{\rm l}*} = \dfrac{{{{({a^{\rm l}} - {b^{\rm l}}c)}^2}{{(1 - 2\beta )}^2}}}{{16{b^{\rm l}}{{(1 - \beta )}^2}}} ,\pi _{{\rm r}4}^{{\rm l}*} = \dfrac{{{{({a^{\rm l}} - {b^{\rm l}}c)}^2}(1 - 3\beta )}}{{16{b^{\rm l}}(1 - \beta )}} 。其中,0 {\text{<}} \beta \leqslant \dfrac{1}{2} 。令\Delta \pi _i^{{\rm l}*} = \pi _{{\rm s}i}^{{\rm l}*} - \pi _{{\rm r}i}^{{\rm l}*} ,结合表1,得\Delta \pi _1^{{\rm l}*} = \dfrac{{{{({a^{\rm l}} - {b^{\rm l}}c)}^2}}}{{16{b^{\rm l}}}} {\text{>}} 0 ,\Delta \pi _2^{{\rm l}*} = \dfrac{{{{({a^{\rm l}} - {b^{\rm l}}c)}^2}{{(1 + \beta )}^2}}}{{16{b^{\rm l}}}} {\text{>}} 0 ,\Delta \pi _3^{{\rm l}*} = \dfrac{{{{({a^{\rm l}} - {b^{\rm l}}c)}^2}(1 - 4{\beta ^2})}}{{16{b^{\rm l}}{{(1 - \beta )}^2}}} {\text{>}} 0 ,\Delta \pi _4^{{\rm l}*} = \dfrac{{{{({a^{\rm l}} - {b^{\rm l}}c)}^2}(1 + 3\beta )}}{{16{b^{\rm l}}(1 - \beta )}} {\text{>}} {\rm{0}} 。易得\Delta \pi _4^{{\rm l}*} {\text{>}} \Delta \pi _1^{{\rm l}*} ,\Delta \pi _4^{{\rm l}*} {\text{>}} \Delta \pi _2^{{\rm l}*} ,\Delta \pi _4^{{\rm l}*} {\text{>}} \Delta \pi _3^{{\rm l}*} 。经过计算,得\pi _{{\rm r}1}^{{\rm n}*} = \dfrac{{a^{\rm n}}{{\rm e}^{ - (2 + {b^{\rm n}}c)}}}{{{b^{\rm n}}}} ,\pi _{{\rm r}2}^{{\rm n}*} = \dfrac{{(1 - \beta) }}{{{b^{\rm n}}}}{a^{\rm n}}{{\rm e}^{ - (2 + {b^{\rm n}}c - \beta )}} ,\pi _{{\rm r}3}^{{\rm n}*} = \dfrac{{a^{\rm n}}{{\rm e}^{ - \left({b^{\rm n}}c + \frac{{2 - \beta }}{{1 - \beta }}\right)}}}{{{b^{\rm n}}}} ,\pi _{{\rm r}4}^{{\rm n}*} = \dfrac{{(1 - 2\beta) }}{{{b^{\rm n}}(1 - \beta )}}{a^{\rm n}}{{\rm e}^{ - (2 + {b^{\rm n}}c)}} 。令\Delta \pi _i^{{\rm n}*} = \pi _{{\rm s}i}^{{\rm n}*} - \pi _{{\rm r}i}^{{\rm n}*} ,结合表2,得\Delta \pi _1^{{\rm n}*} = 0 ,\Delta \pi _2^{{\rm n}*} = \dfrac{\beta }{{{b^{\rm n}}}}{a^{\rm n}}{{\rm e}^{ - (2 + {b^{\rm n}}c - \beta )}} {\text{>}} 0 ,\Delta \pi _3^{{\rm n}*} = \dfrac{\beta a{{\rm e}^{ - \left({b^{\rm n}}c + \frac{{2 - \beta }}{{1 - \beta }}\right)}} }{{{b^{\rm n}}(1 - \beta )}} {\text{>}} 0 ,\Delta \pi _4^{{\rm n}*} = \dfrac{{2\beta a{{\rm e}^{ - (2 + {b^{\rm n}}c)}}}}{{{b^{\rm n}}(1 - \beta )}} {\text{>}} 0 。易得\Delta \pi _4^{{\rm n}*} {\text{>}} \Delta \pi _1^{{\rm n}*} ,\Delta \pi _4^{{\rm n}*} {\text{>}} \Delta \pi _2^{{\rm n}*} ,\Delta \pi _4^{{\rm n}*} {\text{>}} \Delta \pi _3^{{\rm n}*} 。由此得无论在线性需求下还是在非线性需求下,零售商利润总是小于或等于供应商利润,且在供应商采取“激励”策略、零售商采取“偏好利他”策略时利润差达到最大。证毕。一方面,供应商在供应链中占据主导地位,自身具有先动优势,在供应链中总能获取较多的利润。而零售商在供应链中处于被动地位,利润处于弱势,这导致了零售商利润总是小于或等于供应商利润。另一方面,随着供应链关系的稳定发展,零供双方相互关注度增强,此时零售商会采取利他行为让利给供应商,这进一步导致了零售商利润总是小于或等于供应商利润。同时,由于零售商利他偏好会给供应商带来更多利润,当处于信息对称条件时,供应商了解零售商策略,会根据实际情况制定相应的策略使自身利润达到最大。这就导致在供应商采取“激励”策略、零售商采取“偏好利他”策略时,供应商利润最大程度大于零售商利润。
随着时间的推移,供应链成员利他偏好是否会对其均衡策略产生影响,供应链成员利润是否会发生变化,这些都是现实中供应链成员在选择合作伙伴时会考虑的问题。因此,有必要在供应链动态演进特征下研究利他偏好对供应链成员长期均衡策略的影响。
3. 演化博弈分析
演化博弈论是将博弈论和演化理论有机结合起来,主要分析非固定对象经济关系长期稳定趋势的理论,这与供应链中成员企业动态调整、长期合作从而实现整体目标优化保持一致[27]。零售商利他偏好下的零供决策过程是一个动态演化博弈过程且该互动策略调整可以描述为“选择策略—演化—选择新策略—再演化”的演化博弈过程。于是,运用演化博弈理论对零供双方长期内进行单独演化分析、交互演化分析,并将2种需求条件下供应链成员均衡策略进行比较进而研究零售商利他偏好对供应链长期决策的影响。
3.1 线性需求函数下的演化博弈分析
1) 供应商演化博弈分析。由表1可以计算供应商采取“激励”策略的期望收益为
\qquad {E^{{\rm lC}}}(\pi _{\rm s}^{\rm l}) = {y^{\rm l}}\pi _{{\rm s}4}^{{\rm l}*} + (1 - {y^{\rm l}})\pi _{{\rm s}3}^{{\rm l}*} = \dfrac{{{{({a^{\rm l}} - {b^{\rm l}}c)}^2}(1 - 2\beta + {y^{\rm l}}\beta )}}{{8{b^{\rm l}}{{(1 - \beta )}^2}}}{\text{。}} (11) 供应商采取“不激励”策略的期望收益为
\qquad {E^{{\rm lNC}}}(\pi _{\rm s}^{\rm l}) = {y^{\rm l}}\pi _{{\rm s}2}^{{\rm l}*} + (1 - {y^{\rm l}})\pi _{{\rm s}1}^{{\rm l}*} = \dfrac{{{{({a^{\rm l}} - {b^{\rm l}}c)}^2}(1 + {y^{\rm l}}\beta )}}{{8{b^{\rm l}}}}{\text{。}} (12) 由式(11)和(12)可得供应商的平均收益
{\overline E ^{\rm l}}(\pi _{\rm s}^{\rm l}) = {x^{\rm l}}{E^{{\rm lC}}}(\pi _{\rm s}^{\rm l}) + (1 - {x^{\rm l}}){E^{{\rm lNC}}}(\pi _{\rm s}^{\rm l}) 。由此得供应商的复制动态方程
\begin{split} & \qquad {S^{\rm l}}({x^{\rm l}}) = \dfrac{{{\rm{d}}{x^{\rm l}}}}{{{\rm{d}}t}} = {x^{\rm l}}\left[{E^{{\rm lC}}}(\pi _{\rm s}^{\rm l}) - {\overline E ^{\rm l}}(\pi _{\rm s}^{\rm l})\right] = {x^{\rm l}}(1 - {x^{\rm l}}) \times\\ & \left[{E^{{\rm lC}}}(\pi _{\rm s}^{\rm l}) -{E^{{\rm lNC}}}(\pi _{\rm s}^{\rm l})\right]{\text{。}} \end{split} (13) 将各项代入并化简得
\qquad {S^{\rm l}}({x^{\rm l}}) = \dfrac{{{\rm{d}}{x^{\rm l}}}}{{{\rm{d}}t}} = {x^{\rm l}}(1 - {x^{\rm l}})\dfrac{{{{({a^{\rm l}} - {b^{\rm l}}c)}^2}(2{y^{\rm l}} - {y^{\rm l}}\beta - 1){\beta ^2}}}{{8{b^{\rm l}}{{(1 - \beta )}^2}}}{\text{。}} (14) 式中,t表示t时刻。演化博弈的稳定策略要求
{S^{\rm l}}({x^{\rm l}}) = 0 ,{S^{\rm l}}^\prime ({x^{\rm l}}) {\text{<}} 0 。令{S^{\rm l}}({x^{\rm l}}) = 0 ,得到供应商演化博弈的稳定状态为x_1^{{\rm l}*} = 0 ,x_2^{{\rm l}*} = 1 ,{y^{{\rm l}*}} = \dfrac{1}{{2 - \beta }} 。命题3 线性需求函数下,当
{y^{{\rm l}*}} {\text{<}} \dfrac{1}{{2 - \beta }} 时,供应商的演化稳定策略为“不激励”;当{y^{{\rm l}{\rm{*}}}} {\text{>}} \dfrac{1}{{2 - \beta }} 时,供应商的演化稳定策略为“激励”;当{y^{{\rm l}*}} = \dfrac{1}{{2 - \beta }} 时,供应商的任意策略均为稳定状态。证明 令
{S^{\rm l}}({x^{\rm l}}) = 0 ,得到可能存在的稳定状态:x_1^{{\rm l}*} = 0 ,x_2^{{\rm l}*} = 1 ,{y^{{\rm l}*}} = \dfrac{1}{{2 - \beta }} 。对{S^{\rm l}}\left( {{x^{\rm l}}} \right) 求导,得{S^{\rm l}}^\prime ({x^{\rm l}}) = (1 - 2{x^{\rm l}})\dfrac{{{{({a^{\rm l}} - {b^{\rm l}}c)}^2}(2{y^{\rm l}} - {y^{\rm l}}\beta - 1){\beta ^2}}}{{8{b^{\rm l}}{{(1 - \beta )}^2}}} 。当{y^{{\rm l}*}} = \dfrac{1}{{2 - \beta }} 时,{S^{\rm l}}^\prime ({x^{\rm l}}) \equiv 0 ,以{y^{{\rm l}*}} = \dfrac{1}{{2 - \beta }} 为临界点进行讨论。①
{y^{{\rm l}*}} {\text{<}} \dfrac{1}{{2 - \beta }} 时,{S^{\rm l}}^\prime (0) {\text{<}} 0 ,x_1^{{\rm l}*} = 0 为演化博弈稳定解,即供应商演化稳定策略为“不激励”策略。当{y^{{\rm l}*}} {\text{<}} \dfrac{1}{{2 - \beta }} 时,零售商利他偏好越小,选择“激励”策略的供应商越少。由于一开始采取“激励”策略的供应商较少,随着时间的推移,越来越多的供应商会将其策略由“激励”向“不激励”转移,最终所有供应商都会采取“不激励”策略。②
{y^{{\rm l}{\rm{*}}}} {\text{>}} \dfrac{1}{{2 - \beta }} 时,{S^{\rm l}}^\prime (1) {\text{<}} 0 ,x_2^{{\rm l}*} = 1 为演化博弈稳定解,即供应商演化稳定策略为“激励”策略。随着零售商利他偏好程度的增大,越来越多的供应商在制定策略时会考虑零售商利他偏好。当选择“不激励”策略的供应商发现选择“激励”策略的供应商获取了更多利润,随即越来越多的供应商会选择“激励”策略,最终所有供应商都会采取“激励”策略。③
{y^{{\rm l}*}} = \dfrac{1}{{2 - \beta }} 时,{S^{\rm l}}^\prime ({x^{\rm l}}) \equiv 0 ,对于所有的{x^{\rm l}} 都是稳定状态。只要供应链中零售商选择“偏好利他”策略的概率为固定值{y^{{\rm l}*}} = \dfrac{1}{{2 - \beta }} ,供应链中选择“激励”策略的供应商比例和选择“不激励”策略的供应商比例保持不变。此时,对于供应商来说,“激励”策略和“不激励”策略是自身作出的选择,不受零售商利他偏好的影响,即供应商群体内总有{y^{\rm l}} 比例供应商采取“激励”策略,1 - {y^{\rm l}} 比例供应商采取“不激励”策略,且不随时间改变。线性需求函数下,供应商群体的动态趋势和稳定演化过程如图1所示。
2) 零售商演化博弈分析。零售商采取“偏好利他”策略的期望效用为
{E^{{\rm lA}}}(u_{\rm r}^{\rm l}) = {x^{\rm l}}u_{{\rm r}4}^{{\rm l}*} + (1 - {x^{\rm l}})u_{{\rm r}2}^{{\rm l}*} = \\ \dfrac{{{{({a^{\rm l}} - {b^{\rm l}}c)}^2}[(1 - {x^{\rm l}})(2\beta + {\beta ^2}) + 1]}}{{16{b^{\rm l}}}}{\text{。}} (15) 零售商采取“不偏好利他”策略的期望收益为
\begin{split} {E^{{\rm lNA}}}(u_{\rm r}^{\rm l}) = {x^{\rm l}}u_{{\rm r}3}^{{\rm l}*} + (1 - {x^{\rm l}})u_{{\rm r}1}^{{\rm l}*} = \dfrac{{{{({a^{\rm l}} - {b^{\rm l}}c)}^2}[{x^{\rm l}}(3\beta - 2)\beta + {{(1 - \beta )}^2}]}}{{16{b^{\rm l}}{{(1 - \beta )}^2}}}{\text{。}} \end{split} (16) 零售商的平均效用为
\qquad {\overline E ^{\rm l}}(u_{\rm r}^{\rm l}) = {y^{\rm l}}{E^{{\rm lA}}}(u_{\rm r}^{\rm l}) + (1 - {y^{\rm l}}){E^{{\rm lNA}}}(u_{\rm r}^{\rm l}){\text{。}} (17) 由此得
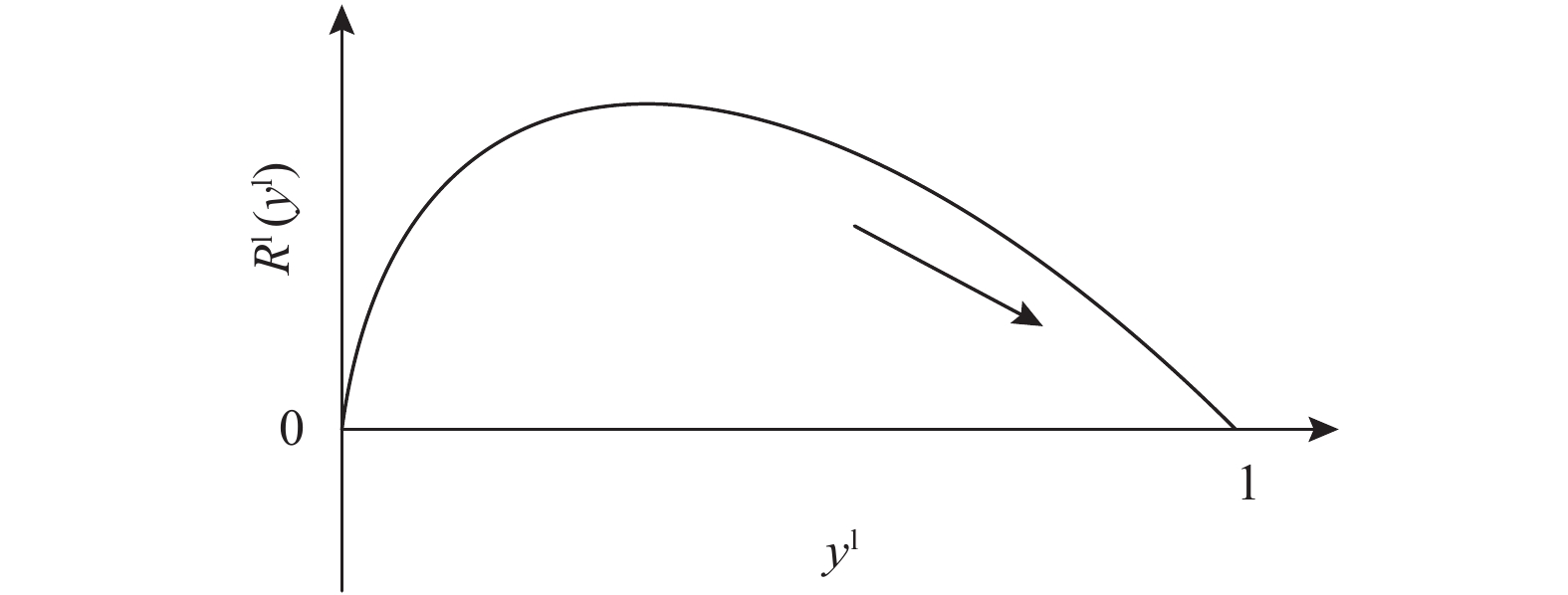
\begin{split} &\qquad{R^{\rm l}}({y^{\rm l}}) = \dfrac{{{\rm{d}}{y^{\rm l}}}}{{{\rm{d}}t}} = {y^{\rm l}}[{E^{{\rm lA}}}(u_{\rm r}^{\rm l}) - {\overline E ^{\rm l}}(u_{\rm r}^{\rm l})] = {y^{\rm l}}(1 - {y^{\rm l}})[{E^{{\rm lA}}}(u_{\rm r}^{\rm l}) - \\ &{E^{{\rm lNA}}}(u_{\rm r}^{\rm l})]{\text{。}} \end{split} (18) 将各表达式代入,得零售商采取“偏好利他”策略的复制动态方程
\qquad {R^{\rm l}}({y^{\rm l}}) = \dfrac{{{\rm{d}}{y^{\rm l}}}}{{{\rm{d}}t}} = {y^{\rm l}}(1 - {y^{\rm l}})\dfrac{{{{({a^{\rm l}} - {b^{\rm l}}c)}^2}[(2 - 3\beta )\beta + (1 - {x^{\rm l}}){\beta ^4}]}}{{16{b^{\rm l}}{{(1 - \beta )}^2}}}{\text{。}} (19) 令
{R^{\rm l}}({y^{\rm l}}) = 0 ,{R^{\rm l}}^\prime ({y^{\rm l}}) {\text{<}} 0 ,得y_1^{{\rm l}*} = 1 是零售商的演化博弈稳定解。命题4 线性需求函数下,零售商的演化稳定策略是采取“偏好利他”策略。
证明 令
{R^{\rm l}}({y^{\rm l}}) = 0 ,得y_1^{{\rm l}*} = 1 ,y_2^{{\rm l}*} = 0 。通过零售商复制动态方程(19)得\qquad {R^{\rm l}}^\prime ({y^{\rm l}}) = (1 - 2{y^{\rm l}})\dfrac{{{{({a^{\rm l}} - {b^{\rm l}}c)}^2}[\beta (2 - 3\beta ) + {\beta ^4}(1 - {x^{\rm l}})]}}{{16{b^{\rm l}}{{(1 - \beta )}^2}}}{\text{。}} 由
{R^{\rm l}}^\prime (0) {\text{>}} 0 ,{R^{\rm l}}^\prime (1) {\text{<}} 0 得,y_1^{{\rm l}*} = 1 为演化博弈稳定解。零供双方在长期合作时,零售商为了维持双方良好的合作伙伴关系,会表现出自身的利他行为。由表1易得u_{{\rm r}3}^{{\rm l}*} {\text{<}} u_{{\rm r}4}^{{\rm l}*} ,u_{{\rm r}1}^{{\rm l}*} {\text{<}} u_{{\rm r}2}^{{\rm l}*} ,即当零售商采取“偏好利他”策略时,零售商能获得更高的效用。当零售商发现选择“偏好利他”策略会给自身带来更高的效用时,他会主动释放善意,帮助自己的合作伙伴。此时,无论供应商是否采取“激励”策略,零售商总会选择“偏好利他”。零售商群体动态趋势和稳定演化过程如图2所示。
3) 双方博弈的交互演化分析。结合供应商和零售商的复制动态方程,可得供应商、零售商博弈过程中交互演化的动力学方程
\qquad \left\{ {\begin{array}{*{20}{l}} {{S^{\rm l}} = \dfrac{{{\rm{d}}{x^{\rm l}}}}{{{\rm{d}}t}} = {x^{\rm l}}(1 - {x^{\rm l}})\dfrac{{{{({a^{\rm l}} - {b^{\rm l}}c)}^2}[{y^{\rm l}}(2 - \beta ) - 1]{\beta ^2}}}{{8{b^{\rm l}}{{(1 - \beta )}^2}}}}, \\ {{R^{\rm l}} = \dfrac{{{\rm{d}}{y^{\rm l}}}}{{{\rm{d}}t}} = {y^{\rm l}}(1 - {y^{\rm l}})\dfrac{{{{({a^{\rm l}} - {b^{\rm l}}c)}^2}[\beta (2 - 3\beta ) + (1 - {x^{\rm l}}){\beta ^4}]}}{{16{b^{\rm l}}{{(1 - \beta )}^2}}}} {\text{。}} \end{array}} \right. (20) 根据Friedman[27]提出的方法,稳定均衡点可由雅可比矩阵的局部稳定性分析得到。式(20)的雅克比矩阵
{\boldsymbol{J}} = \left[ {\begin{array}{*{20}{l}} {{J_1}}&{{J_2}} \\ {{J_3}}&{{J_4}} \end{array}} \right] 。其中,各个符号表达式如下。\qquad J_1^{\rm l} = \dfrac{{\partial {S^{\rm l}}}}{{\partial {x^{\rm l}}}} = (1 - 2{x^{\rm l}})\dfrac{{{{({a^{\rm l}} - {b^{\rm l}}c)}^2}[{y^{\rm l}}(2 - \beta ) - 1]{\beta ^2}}}{{8{b^{\rm l}}{{(1 - \beta )}^2}}}; \qquad J_2^{\rm l} = \dfrac{{\partial {S^{\rm l}}}}{{\partial {y^{\rm l}}}} = {x^{\rm l}}(1 - {x^{\rm l}})\dfrac{{{{({a^{\rm l}} - {b^{\rm l}}c)}^2}(2 - \beta ){\beta ^2}}}{{8{b^{\rm l}}{{(1 - \beta )}^2}}}; \qquad J_3^{\rm l} = \dfrac{{\partial {R^{\rm l}}}}{{\partial {x^{\rm l}}}} = - {y^{\rm l}}(1 - {y^{\rm l}})\dfrac{{{{({a^{\rm l}} - {b^{\rm l}}c)}^2}{\beta ^4}}}{{16{b^{\rm l}}{{(1 - \beta )}^2}}}; \qquad J_4^{\rm l} = \dfrac{{\partial {R^{\rm l}}}}{{\partial {y^{\rm l}}}} = (1 - 2{y^{\rm l}})\dfrac{{{{({a^{\rm l}} - {b^{\rm l}}c)}^2}[\beta (2 - 3\beta ) + (1 - {x^{\rm l}}){\beta ^4}]}}{{16{b^{\rm l}}{{(1 - \beta )}^2}}}{\text{。}} 雅可比矩阵
{\boldsymbol{J}} 对应行列式值为{\rm{Det}}({\boldsymbol{J}}) = {J_1}{J_4} - {J_2}{J_3} ,迹为{\rm{Tr}}({\boldsymbol{J}}) = {J_1} + {J_4} 。根据雅可比矩阵的局部稳定性理论,当动态演化系统中某个稳定点满足{\rm{Det}}({\boldsymbol{J}}) {\text{>}} 0 且{\rm{Tr}}({\boldsymbol{J}}) {\text{<}} 0 ,此时为动态系统的演化稳定策略(evolutionary stability strategy,{\rm{ESS}} );当{\rm{Det}}({\boldsymbol{J}}) {\text{<}} 0 时,该点则为鞍点;其余均为不稳定点。令
m = 1 - \beta ,f = \dfrac{{{{({a^{\rm l}} - {b^{\rm l}}c)}^2}{\beta ^2}}}{{8{b^{\rm l}}{{(1 - \beta )}^2}}} ,j = \dfrac{{{{({a^{\rm l}} - {b^{\rm l}}c)}^2}}}{{16{b^{\rm l}}{{(1 - \beta )}^2}}} ,h = \beta (2 - 3\beta ) + {\beta ^4} ,得到均衡点的稳定性分析结果,如表3所示。根据上述分析,可得演化稳定相位图,如图3所示。表 3 均衡点的局部均衡稳定性分析1)Table 3. The stable analysis of each local equilibrium point均衡点 {\rm{Det}}({\boldsymbol{J}}) {\rm{Tr}}({\boldsymbol{J}}) 稳定性 {x^{\rm l}} = 0, {y^{\rm l}} = 0 - fjh - - f + jh A,+ 鞍点 B, 0 C, − {x^{\rm l}} = 1, {y^{\rm l}} = 0 fj(h - {\beta ^4}) + f + j(h - {\beta ^4}) + 不稳
定点{x^{\rm l}} = 0, {y^{\rm l}} = 1 - fmjh - fm - jh - 鞍点 {x^{\rm l}} = 1, {y^{\rm l}} = 1 fmj(h - {\beta ^4}) + - fm - j(h - {\beta ^4}) - {\rm{ESS}} 1) A: 0 \leqslant \beta < \sqrt 2 - 1; B: \beta = \sqrt 2 - 1; C: \sqrt 2 - 1 < \beta \leqslant \dfrac{1}{2} 3.2 非线性需求函数下的演化博弈分析
1) 供应商演化博弈分析。根据表2,供应商采取“激励”策略的期望收益为
\begin{array}{l} \qquad {E^{{\rm nC}}}(\pi _{\rm s}^{\rm n}) = {y^{\rm n}}\pi _{{\rm s}4}^{{\rm n}*}{\rm{ + }}(1 - {y^{\rm n}})\pi _{{\rm s}3}^{{\rm n}*} = \dfrac{{[{y^{\rm n}} + (1 - {y^{\rm n}}){{\rm e}^{ - \frac{\beta }{{1 - \beta }}}}]}}{{{b^{\rm n}}(1 - \beta )}}{a^{\rm n}}{{\rm e}^{ - (2 + {b^{\rm n}}c)}}{\text{。}} \end{array} (21) 供应商采取“不激励”策略的期望收益为
\begin{array}{l} \qquad {E^{{\rm nNC}}}(\pi _{\rm s}^{\rm n}) = {y^{\rm n}}\pi _{{\rm s}2}^{{\rm n}*}{\rm{ + }}(1 - {y^{\rm n}})\pi _{{\rm s}1}^{{\rm n}*} = \dfrac{{1 - {y^{\rm n}} + {y^{\rm n}}{{\rm e}^\beta }}}{{{b^{\rm n}}}}{a^{\rm n}}{{\rm e}^{ - (2 + {b^{\rm n}}c)}}{\text{。}} \end{array} (22) 供应商的平均收益为
\qquad {\overline E ^{\rm n}}(\pi _{\rm s}^{\rm n}) = {x^{\rm n}}{E^{{\rm nC}}}(\pi _{\rm s}^{\rm n}) + (1 - {x^{\rm n}}){E^{{\rm nNC}}}(\pi _{\rm s}^{\rm n}){\text{。}} (23) 由
{S^{\rm n}}({x^{\rm n}}) = \dfrac{{{\rm{d}}{x^{\rm n}}}}{{{\rm{d}}t}} = {x^{\rm n}}[{E^{{\rm nC}}}(\pi _{\rm s}^{\rm n}) - {\overline E ^{\rm n}}(\pi _{\rm s}^{\rm n})] 得供应商的复制动态方程\begin{split} &\qquad {S^{\rm n}}({x^{\rm n}}) = {x^{\rm n}}(1 - {x^{\rm n}}){a^{\rm n}}{{\rm e}^{ - (2 + {b^{\rm n}}c)}} \left[\dfrac{{{y^{\rm n}}(2 - \beta - {{\rm e}^\beta }) - 1}}{{{b^{\rm n}}(1 - \beta )}}+ \right.\\ & \left.\dfrac{{(1 - {y^{\rm n}}){{\rm e}^{ - \frac{\beta }{{1 - \beta }}}} + (1 + {y^{\rm n}}{{\rm e}^\beta })\beta }}{{{b^{\rm n}}(1 - \beta )}}\right]{\text{。}} \end{split} (24) 令
{S^{\rm n}}({x^{\rm n}}) = 0 ,得可能存在的稳定状态x_1^{{\rm n}*} = 0 ,x_2^{{\rm n}*} = 1 ,{y^{{\rm n}*}} = \dfrac{{1 - \beta - {{\rm e}^{ - \frac{\beta }{{1 - \beta }}}}}}{{2 - \beta - {{\rm e}^{ - \frac{\beta }{{1 - \beta }}}} - (1 - \beta ){{\rm e}^\beta }}} 。令
M = \dfrac{{1 - \beta - {{\rm e}^{ - \frac{\beta }{{1 - \beta }}}}}}{{2 - \beta - {{\rm e}^{ - \frac{\beta }{{1 - \beta }}}} - (1 - \beta ){{\rm e}^\beta }}} ,对供应商的复制动态方程进行演化分析,可以得到命题5。命题5 非线性需求函数下:当
{y^{{\rm n}*}} {\text{<}} M 时,供应商演化稳定策略为“不激励”策略;当{y^{{\rm n}*}} {\text{>}} M 时,供应商演化稳定策略为“激励”策略;当{y^{{\rm n}*}} = M 时,供应链中选择“激励”和“不激励”的供应商比例保持不变。证明 由式(24)得,
{S^{\rm n}}^\prime ({x^{\rm n}})\; =\; (1 \;-\; 2{x^{\rm n}}){a^{\rm n}}{{\rm e}^{ - (2 + {b^{\rm n}}c)}} \times \left[\dfrac{{{y^{\rm n}}(2 - \beta - {{\rm e}^\beta }) - 1}}{{{b^{\rm n}}(1 - \beta )}} + \right.\left. {\rm{ }} \dfrac{{(1 - {y^{\rm n}}){{\rm e}^{ - \frac{\beta }{{1 - \beta }}}} (1 + {y^{\rm n}}{{\rm e}^\beta })\beta }}{{{b^{\rm n}}(1 - \beta )}}\right] 。令
{S^{\rm n}}({x^{\rm n}}) = 0 ,得x_1^{{\rm n}*} = 0 ,x_2^{{\rm n}*} = 1 ,{y^{{\rm n}*}} = M 。当{y^{{\rm n}*}} = M 时,{S^{\rm n}}^\prime ({x^{\rm n}}) \equiv 0 ,故以M 为临界点进行讨论。①
{y^{{\rm n}*}} {\text{<}} M 时,{S^{\rm n}}^\prime (0) {\text{<}} 0 ,此时x_1^{{\rm n}*} = 0 为演化博弈稳定解,即供应商演化稳定策略为“不激励”策略。{y^{{\rm n}*}} {\text{<}} M 时,供应商对零售商的利他行为不予重视,认为零售商只关注自身利润的获取。此时,所有供应商最终都会选择“不激励”策略。②
{y^{{\rm n}*}} {\text{>}} M 时,{S^{\rm n}}^\prime (1) {\text{<}} 0 ,此时x_2^{{\rm n}*} = 1 为演化博弈稳定解,即供应商演化稳定策略为“激励”策略。此时选择“不激励”策略的供应商发现零售商利他偏好会给自身带来更多利润,同时他们发现一开始选择“激励”策略的供应商销量更大、利润更多,随即越来越多的供应商会选择“激励”策略,最终所有供应商都会选择“激励”策略。③
{y^{{\rm n}*}} = M 时,{S^{\rm n}}^\prime ({x^{\rm n}}) \equiv 0 ,此时所有{x^{\rm n}} 都是稳定状态。当零售商选择“偏好利他”的概率为固定值{y^{{\rm n}*}} = M ,供应链中选择“激励”和“不激励”的供应商比例就会保持不变,即供应链中总有{x^{\rm n}} 比例供应商采取“激励”策略,1 - {x^{\rm n}} 比例供应商采取“不激励”策略。供应商群体的动态趋势和演化过程如图4所示。
结论3 通过对供应商的单独演化分析发现,无论在线性需求函数还是非线性需求函数下,供应商是否采取“激励”策略依赖于选择“偏好利他”的零售商比例。
证明 由命题3和命题5即可得证。无论在线性需求还是非线性需求下,当选择“偏好利他”的零售商比例发生变化时,供应商演化稳定策略也会发生改变,即供应商的演化稳定策略依赖于选择“偏好利他”的零售商比例。虽然在供应链中供应商具有先行决策的优势,但零售商更靠近终端市场,更了解消费者需求,所以长期博弈时,供应商的演化稳定策略会受到零售商“利他偏好”的影响。一方面,由于企业间的合作往往需要经历长期博弈和反复调整才能达到双方的稳定状态。随着供应链关系的稳定发展,供应商对零售商群体关注度逐渐增强,会根据零售商群体的策略情况对自身策略进行调整。另一方面,供应商始终以自身利润最大化为目标,当发现零售商选择“偏好利他”策略的比例会对自身利润造成影响时,为使利润最大化,会根据零售商群体中采取“偏好利他”策略的零售商比例制定自身策略,获取更多利润。这导致长期博弈时,无论在线性需求还是非线性需求下,供应商是否采取“激励”策略依赖于选择“偏好利他”的零售商比例。
2) 零售商演化博弈分析。零售商采取“偏好利他”策略的期望效用为
\qquad {E^{{\rm nA}}}(u_{\rm r}^{\rm n}) = {x^{\rm n}}u_{{\rm r}4}^{{\rm n}*} + (1 - {x^{\rm n}})u_{{\rm r}2}^{{\rm n}*} = \dfrac{{{x^{\rm n}} + (1 - {x^{\rm n}}){{\rm e}^\beta }}}{{{b^{\rm n}}}}{a^{\rm n}}{{\rm e}^{ - (2 + {b^{\rm n}}c)}}{\text{。}} (25) 零售商采取“不偏好利他”策略的期望收益为
\begin{split} &\qquad{E^{{\rm nNA}}}(u_{\rm r}^{\rm n}) = {x^{\rm n}}u_{{\rm r}3}^{{\rm n}*} + (1 - {x^{\rm n}})u_{{\rm r}1}^{{\rm n}*} = \dfrac{{{x^{\rm n}}{{\rm e}^2} + (1 - {x^{\rm n}}){{\rm e}^{\frac{{2 - \beta }}{{1 - \beta }}}}}}{{{b^{\rm n}}}}\times\\ &{a^{\rm n}}{{\rm e}^{ - \left(2 + {b^{\rm n}}c + \frac{{2 - \beta }}{{1 - \beta }}\right)}}{\text{。}} \end{split} (26) 零售商的平均效用
{\overline E ^{\rm n}}(u_{\rm r}^{\rm n}) = {y^{\rm n}}{E^{{\rm nA}}}(u_{\rm r}^{\rm n}) + (1 - {y^{\rm n}})\times {E^{{\rm nNA}}}(u_{\rm r}^{\rm n}) 。由
{R^{\rm n}}({y^{\rm n}}) = {y^{\rm n}}[{E^{{\rm nA}}}(u_{\rm r}^{\rm n}) - {\overline E ^{\rm n}}(u_{\rm r}^{\rm n})] 得零售商的复制动态方程\begin{split} &\qquad {R^{\rm n}}({y^{\rm n}}) = {y^{\rm n}}(1 - {y^{\rm n}}){a^{\rm n}}{{\rm e}^{ - \left(2 + {b^{\rm n}}c + \frac{{2 - \beta }}{{1 - \beta }}\right)}} \left[\dfrac{{(2{x^{\rm n}} - 1){{\rm e}^{\frac{{2 - \beta }}{{1 - \beta }}}}}}{{{b^{\rm n}}}} + \right.\\[-2pt] &\left. \dfrac{{(1 - {x^{\rm n}}){{\rm e}^{\frac{{2 - {\beta ^2}}}{{1 - \beta }}}} - {x^{\rm n}}{{\rm e}^2}}}{{{b^{\rm n}}}}\right]{\text{。}} \end{split} (27) 令
{R^{\rm n}}({y^{\rm n}}) = 0 ,得到可能存在的稳定状态y_1^{{\rm n}*} = 0 ,y_2^{{\rm n}*} = 1 ,{x^{{\rm n}*}} = \dfrac{{{{\rm e}^{\frac{{2 - \beta }}{{1 - \beta }}}} - {{\rm e}^{\frac{{2 - {\beta ^2}}}{{1 - \beta }}}}}}{{2{{\rm e}^{\frac{{2 - \beta }}{{1 - \beta }}}} - {{\rm e}^{\frac{{2 - {\beta ^2}}}{{1 - \beta }}}} - {{\rm e}^2}}} 。令Z = (2{x^{\rm n}} - 1){{\rm e}^{\frac{{2 - \beta }}{{1 - \beta }}}} + (1 - {x^{\rm n}})\times {{\rm e}^{\frac{{2 - {\beta ^2}}}{{1 - \beta }}}} - {x^{\rm n}}{{\rm e}^2} ,N = \dfrac{{{{\rm e}^{\frac{{2 - \beta }}{{1 - \beta }}}} - {{\rm e}^{\frac{{2 - {\beta ^2}}}{{1 - \beta }}}}}}{{2{{\rm e}^{\frac{{2 - \beta }}{{1 - \beta }}}} - {{\rm e}^{\frac{{2 - {\beta ^2}}}{{1 - \beta }}}} - {{\rm e}^2}}} 。对零售商复制动态方程进行演化分析,得命题6。
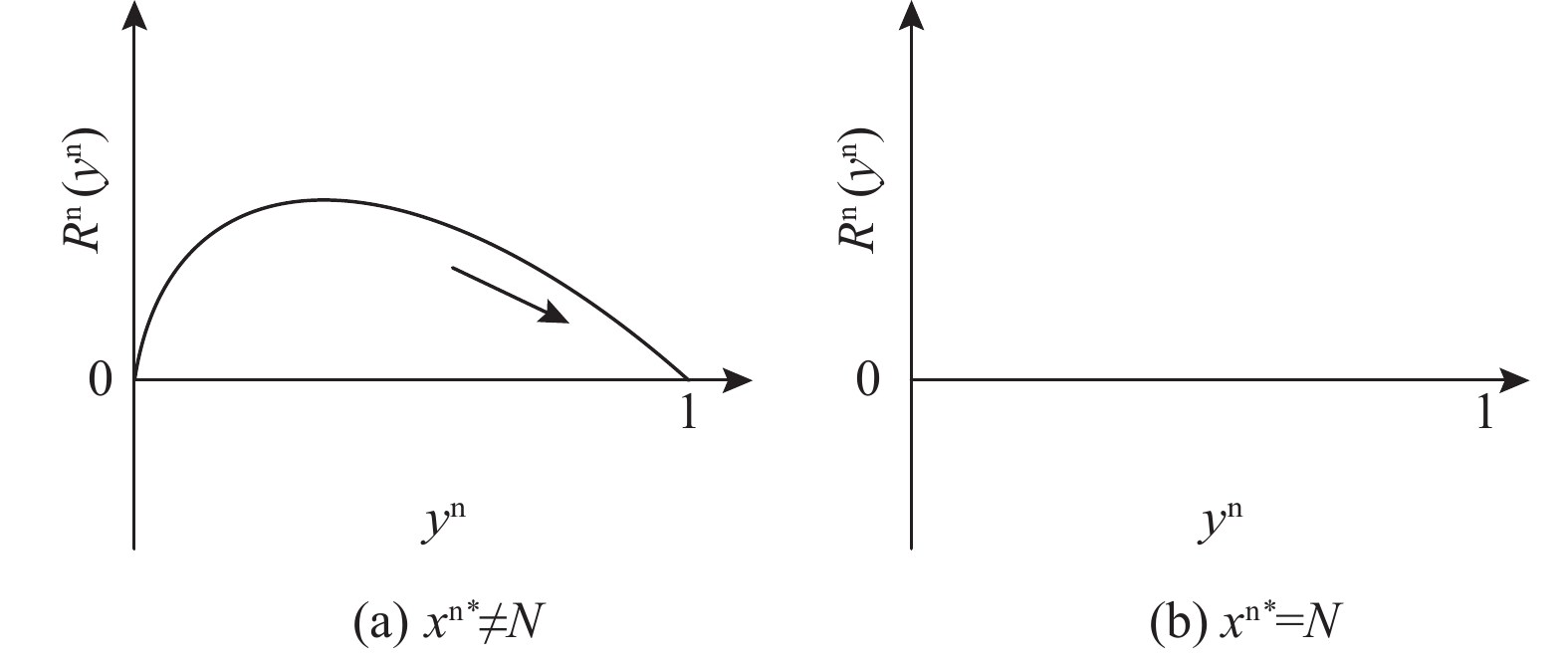
命题6 非线性需求函数下,当
{x^{{\rm n}*}} \ne N 时,零售商演化稳定策略为“偏好利他”策略;当{x^{{\rm n}*}} = N 时,零售商群体里选择“偏好利他”和“不偏好利他”的零售商比例保持不变。证明 由式(27)得
{R^{\rm n}}^\prime ({y^{\rm n}}) = (1 - 2{y^{\rm n}})\dfrac{Z}{{{b^{\rm n}}}}{a^{\rm n}}{{\rm e}^{ - (2 + {b^{\rm n}}c + \frac{{2 - \beta }}{{1 - \beta }})}} 。其中
Z \geqslant 0 。演化博弈稳定策略要求同时满足{R^{\rm n}}({y^{\rm n}}) = 0 ,{R^{\rm n}}^\prime ({y^{\rm n}}) {\text{<}} 0 。当{x^{{\rm n}*}} = N 时,{R^{\rm n}}^\prime ({y^{\rm n}}) \equiv 0 ,故以N 为临界点进行讨论。①当
{x^{{\rm n}*}} \ne N 时,{R^{\rm n}}^\prime (1) {\text{<}} 0 ,此时y_2^{{\rm n}*} = 1 为演化博弈稳定解,即零售商演化稳定策略为“偏好利他”策略。零售商在供应链中处被动地位,更愿意通过自身的利他行为表现出自己的诚意,促进双方长期合作,以使自身得到更高的效用。当{x^{{\rm n}*}} \ne N 时,最初采取“不偏好利他”的零售商发现采取“偏好利他”的零售商通过自己的利他行为获得了更高的效用,越来越多的零售商会选择采取“偏好利他”策略,最终所有零售商都会采取“偏好利他”策略。②当
{x^{{\rm n}*}} = N 时,{R^{\rm n}}^\prime ({y^{\rm n}}) \equiv 0 。所有{y^{\rm n}} 都是稳定状态。只要供应商群体里选择“激励”策略的供应商比例为固定值{x^{{\rm n}*}} = N ,选择“偏好利他”和“不偏好利他”的零售商比例保持不变,且不随时间变化。对零售商而言,供应链中总有{x^{{\rm n}*}} 比例零售商采取“偏好利他”策略,1 - {x^{{\rm n}*}} 比例零售商采取“不偏好利他”策略。零售商群体的动态趋势和稳定演化过程如图5所示。3)双方博弈的交互演化分析。令
d = \dfrac{{{a^{\rm n}}{{\rm e}^{ - (2 + {b^{\rm n}}c + \frac{{2 - \beta }}{{1 - \beta }})}}}}{{{b^{\rm n}}}} ,g = \dfrac{{{a^{\rm n}}{{\rm e}^{ - (2 + {b^{\rm n}}c)}}}}{{{b^{\rm n}}(1 - \beta )}} 。结合供应商和零售商的复制动态方程,可得供应商、零售商博弈过程中交互演化的动力学方程\begin{split} \qquad\left\{ {\begin{array}{*{20}{l}} {S^{\rm n}}({x^{\rm n}}) = {x^{\rm n}}(1 - {x^{\rm n}})g \left[{y^{\rm n}}(2 - \beta - {{\rm e}^\beta }) - 1 + (1 - {y^{\rm n}}){{\rm e}^{ - \frac{\beta }{{1 - \beta }}}} +\right.\\ \bigg. (1 + {y^{\rm n}}{{\rm e}^\beta })\beta \bigg] ;\\ {R^{\rm n}}({y^{\rm n}}) = {y^{\rm n}}(1 - {y^{\rm n}})d \left[(2{x^{\rm n}} - 1){{\rm e}^{\frac{{2 - \beta }}{{1 - \beta }}}} {\rm{ }} + (1 - {x^{\rm n}}){{\rm e}^{\frac{{2 - {\beta ^2}}}{{1 - \beta }}}} - {x^{\rm n}}{{\rm e}^2} \right] {\text{。}} \end{array}} \right. \end{split} (28) 式(28)的雅克比矩阵中各个符号表达式分别为
\begin{split} &\qquad J_1^{\rm n} = \dfrac{{\partial {S^{\rm n}}}}{{\partial {x^{\rm n}}}} = (1 - 2{x^{\rm n}})g \left[{y^{\rm n}}(2 - \beta - {{\rm e}^\beta }) - 1+ (1 - {y^{\rm n}}){{\rm e}^{ - \frac{\beta }{{1 - \beta }}}} +\right.\\ &\bigg.(1 + {y^{\rm n}}{{\rm e}^\beta })\beta \bigg]; \end{split} \qquad J_2^{\rm n} = \dfrac{{\partial {S^{\rm n}}}}{{\partial {y^{\rm n}}}} = {x^{\rm n}}(1 - {x^{\rm n}})g \left[1 - {{\rm e}^{ - \frac{\beta }{{1 - \beta }}}} + (1 - {{\rm e}^\beta })(1 - \beta ) \right]; \qquad J_3^{\rm n} = \dfrac{{\partial {R^{\rm n}}}}{{\partial {x^{\rm n}}}} = {y^{\rm n}}(1 - {y^{\rm n}})d \left[2{{\rm e}^{\frac{{2 - \beta }}{{1 - \beta }}}} - {{\rm e}^{\frac{{2 - {\beta ^2}}}{{1 - \beta }}}} - {{\rm e}^2} \right]; \qquad J_4^{\rm n} = \dfrac{{\partial {R^{\rm n}}}}{{\partial {y^{\rm n}}}} = (1 - 2{y^{\rm n}})d \left[(2{x^{\rm n}} - 1){{\rm e}^{\frac{{2 - \beta }}{{1 - \beta }}}} + (1 - {x^{\rm n}}){{\rm e}^{\frac{{2 - {\beta ^2}}}{{1 - \beta }}}} - {x^{\rm n}}{{\rm e}^2} \right]{\text{。}} 雅可比矩阵
{\boldsymbol{J}} 对应行列式值为{\rm{Det}}({\boldsymbol{J}}) = {J_1}{J_4} - {J_2}{J_3} ,迹为{\rm{Tr}}({\boldsymbol{J}}) = {J_1} + {J_4} 。对动力学方程组(28)进行分析,可得供应链系统的均衡点为(0,0) 、(1,0) 、(0,1) 、(1,1) 、(N,M) 。令
s = {{\rm e}^{ - \frac{{2 - \beta }}{{1 - \beta }}}} \left({{\rm e}^{\frac{{2 - {\beta ^2}}}{{1 - \beta }}}} - {{\rm e}^{\frac{{2 - \beta }}{{1 - \beta }}}} \right) ,v = {{\rm e}^{ - \frac{{2 - \beta }}{{1 - \beta }}}} \left({{\rm e}^{\frac{{2 - \beta }}{{1 - \beta }}}} - {{\rm e}^2} \right) ,r = - 1{\rm{ + }} \beta + {{\rm e}^{ - \frac{\beta }{{1 - \beta }}}} ,{\textit{z}} = 1 - {{\rm e}^\beta } + {{\rm e}^\beta }\beta ,k = 1 - \beta 。可得均衡点的稳定性分析结果如表4所示。根据上述分析,可得演化稳定相位图,如图6所示。表 4 均衡点的局部均衡稳定性分析Table 4. The stable analysis of each local equilibrium point均衡点 {\rm{Det}}({\boldsymbol{J}}) {\rm{Tr}}({\boldsymbol{J}}) 稳定性 x = 0, y = 0 {g^2}ksr - g(ks + r) + 鞍点 x = 1, y = 0 - {g^2}kvr + g(kv - r) + 不稳定点 x = 0, y = 1 - {g^2}ksz - g( - ks + z) - 鞍点 x = 1, y = 1 {g^2}kvz + - g(kv + z) - {\rm{ESS}} x = N, y = M - {g^2}k\dfrac{{svrz}}{{(s - v)(r - z)}} - 0 0 鞍点 结论4 无论在线性需求函数还是非线性需求函数条件下,供应链长期均衡策略均为零售商采取“偏好利他”策略,供应商采取“激励”策略。
无论在线性需求函数还是在非线性需求函数下,长期内零售商均以包括自身利润和利他偏好正效用在内的总效用最大化为目标制定自身零售价格。现实中,零售商作为跟随者,会通过自身利他行为表现出合作共赢意愿,以促进双方维持稳定的长期合作。零供双方长期博弈时,零售商会接受供应商制定的较高的批发价格从而让利给供应商,以保持稳定的合作关系。同时,为避免自身效用降低,零售商会采取“偏好利他”策略使自身效用达到最大。而供应商作为供应链的主导者,具有先动优势,不用降低批发价格就可以获得足够多的利润,且当其采取“激励”策略时,供应商利润达到最大。所以,无论线性需求函数还是非线性需求函数下,供应链长期均衡策略均为零售商采取“偏好利他”策略,供应商采取“激励”策略。
4. Matlab数值仿真分析
为更直观地反映不同市场需求下供应商和零售商的策略选择,更直观地说明上述结论并验证供应链的稳定均衡策略,依据本文构建的Stackelberg演化博弈模型和算法,运用Matlab演化仿真对上文计算的演化稳定性进行仿真分析。
4.1 线性需求函数下的数值仿真分析
根据上文有关参数取值范围的限制条件,取
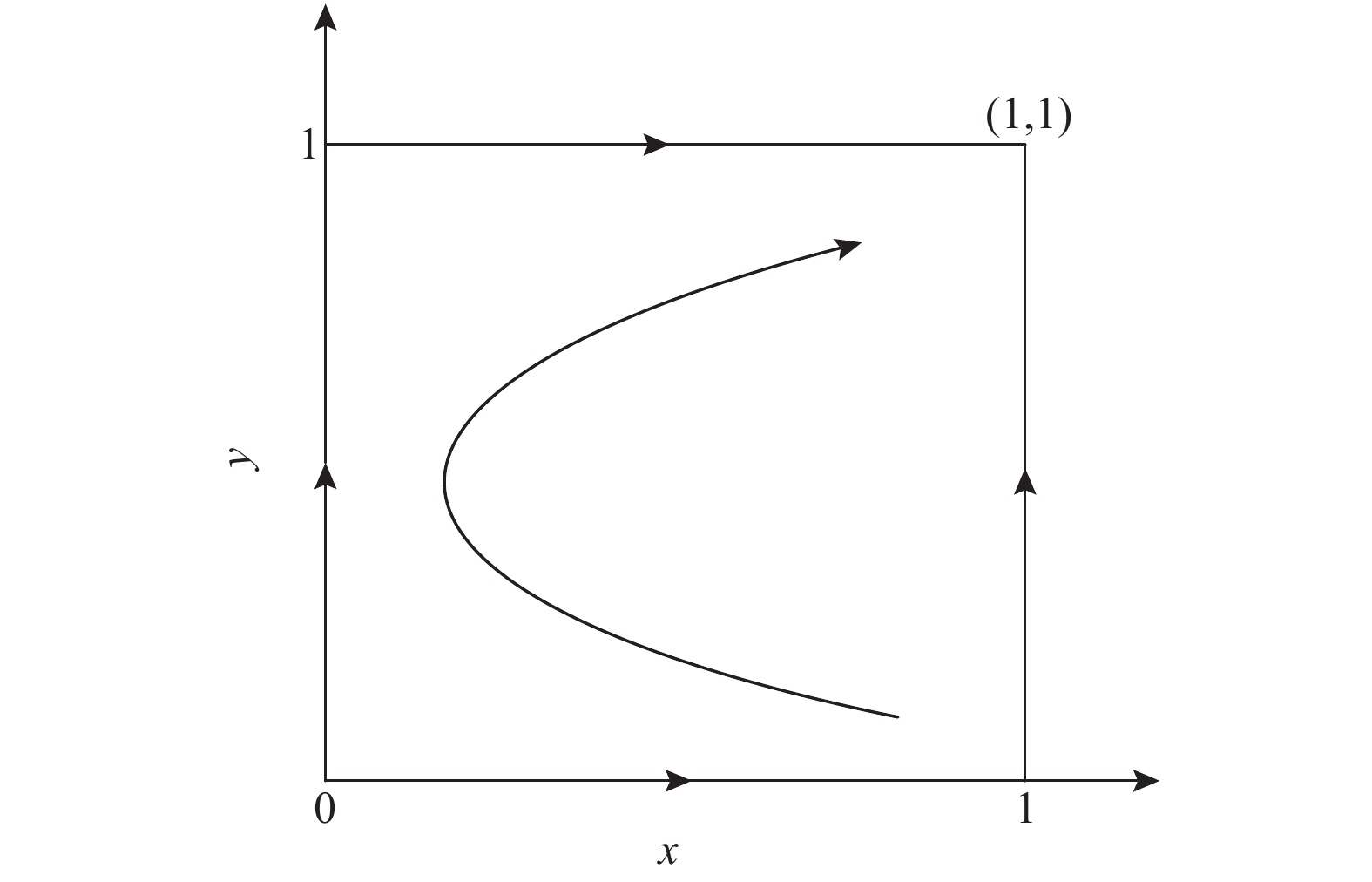
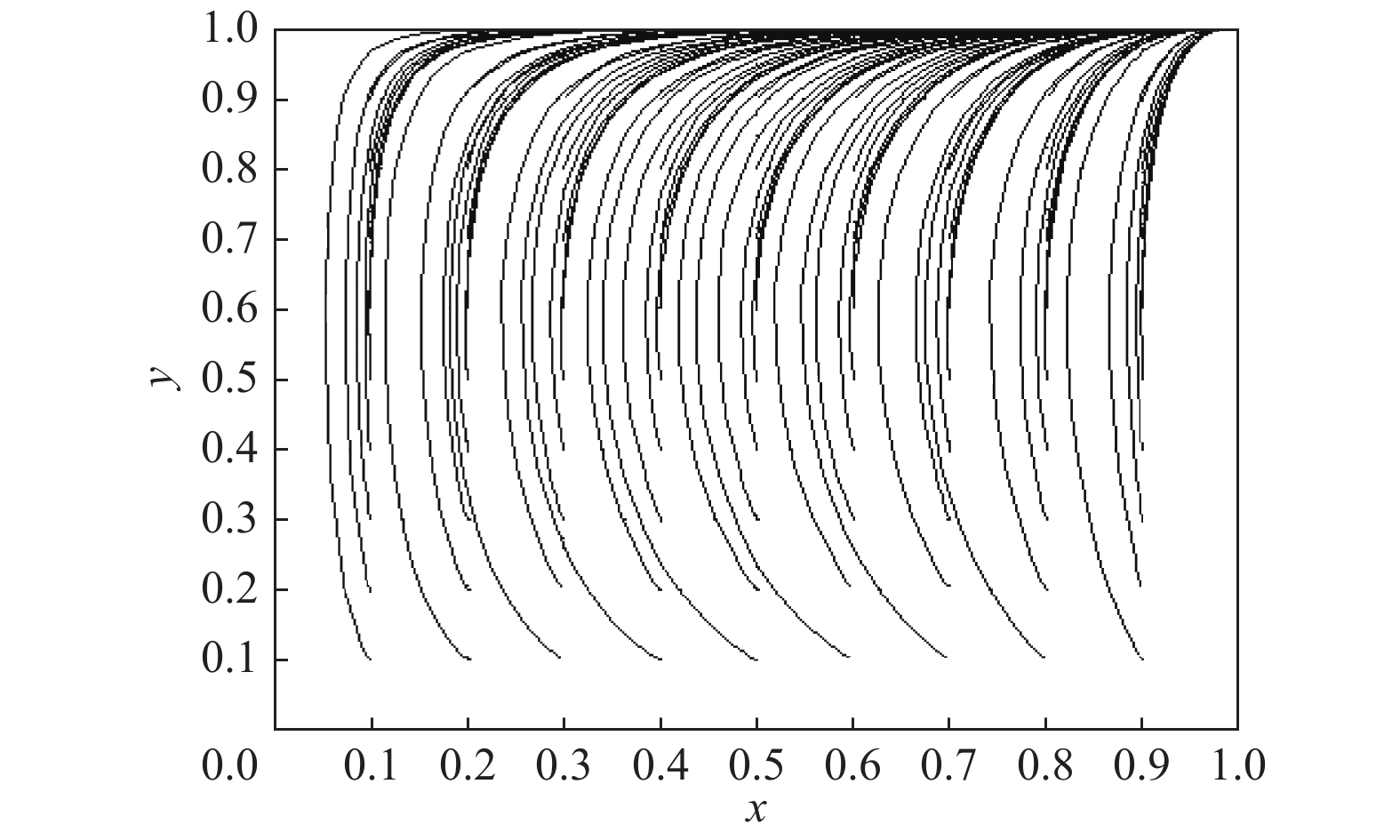
{a^{\rm l}} = 500 ,{b^{\rm l}} = 25 ,c = 10 ,\;\beta = 0.3 ,得供应商、零售商博弈过程中交互演化的动力学方程\begin{split} \qquad \left\{ {\begin{array}{*{20}{l}} {{S^{\rm l}} = \dfrac{{{\rm{d}}{x^{\rm l}}}}{{{\rm{d}}t}} = 57.398{x^{\rm l}}(1 - {x^{\rm l}})(1.7{y^{\rm l}} - 1)} ;\\ {{R^{\rm l}} = \dfrac{{{\rm{d}}{y^{\rm l}}}}{{{\rm{d}}t}} = 318.878{y^{\rm l}}(1 - {y^{\rm l}})(0.338\;1 - 0.008\;1{x^{\rm l}})} {\text{。}} \end{array}} \right. \end{split} 经Matlab数值仿真分析,线性需求函数下供应商和零售商策略选择的演化路径,如图7所示。
由图7可得线性函数需求下供应商和零售商的演化稳定策略为(激励,偏好利他),即所有的点最终都收敛于(1,1),与结论4一致。这表示在线性需求下,供应链长期均衡的结果为供应商采取“激励”策略,零售商采取“偏好利他”策略。
供应商作为供应链的主导者,不用降低自身批发价格就可以获得足够多的的利润。当供应商采取“激励”策略时,总能达到自身利润的最大值,所以它总是会采取“激励”策略。而在供应链中,零售商地位较低,为了维持与主导者之间的长期合作,在制定决策时会表现出利他行为,考虑供应商利润。由于“偏好利他”策略总能给零售商带来更高的效用,所以即使刚开始有少量零售商采取“不偏好利他”策略,随着时间的推移,所有零售商最终都会采取“偏好利他”策略。
4.2 非线性需求函数下的数值仿真分析
根据上文有关参数取值范围的限制条件,取
{a^{\rm n}} = 100 ,{b^{\rm n}} = 0.2 ,c = 10 ,\;\beta = 0.3 ,可得非线性需求下供应商、零售商博弈过程中交互演化的动力学方程\begin{split} \qquad \left\{ {\begin{array}{*{20}{l}} {{S^{\rm n}} = \dfrac{{{\rm{d}}{x^{\rm n}}}}{{{\rm{d}}t}} = 13.083{x^{\rm n}}(1 - {x^{\rm n}})(0.104{y^{\rm n}} - 0.486)}; \\ {{R^{\rm n}} = \dfrac{{{\rm{d}}{y^{\rm n}}}}{{{\rm{d}}t}} = 0.807{y^{\rm n}}(1 - {y^{\rm n}})(3.968 - 0.015{x^{\rm n}})} {\text{。}} \end{array}} \right. \end{split} 经Matlab数值仿真分析,非线性需求函数下供应商和零售商策略选择的演化路径如图8所示。
由图8可以发现非线性需求函数下零供双方的策略选择演化路径图中所有的点最终都收敛于(1,1),即在长期的动态变化中,供应商和零售商策略选择趋于(激励,偏好利他)。
由于供应商在博弈中具有先行行动优势,能够看到零售商的反应函数从而作出最有利于自身的决策,获得更多的利润。长期条件下,供应商会选择采取“激励”策略,制定较高的批发价格保证自身利润最大。同时,在供应链中,合作才能整体利益最大化,所以在长期条件下,零售商会主动表现出自己的利他行为以促进双方合作,即零售商会采取“偏好利他”策略。当零售商采取“偏好利他”策略时,零售商自身效用达到最大,所以非线性函数需求下供应链长期均衡策略是供应商采取“激励”策略,零售商采取“偏好利他”策略。
5. 总结
本文考虑供应链成员的利他偏好行为和供应链动态演化特征,研究零售商利他偏好对供应链成员决策的影响。分别在线性需求函数和非线性需求函数条件下分析短期内零供双方的均衡稳定策略,同时对长期内零供双方的单独演化博弈和交互演化博弈进行对比。研究发现,1) 短期内,2种需求条件下供应商均衡策略均依赖于零售商策略,而零售商均衡策略不受供应商影响且均为“偏好利他”;2) 短期内,2种需求条件下零售商利润总是不大于供应商利润,且当零售商采取“偏好利他”策略、供应商采取“激励”策略时,零供利润差达到最大;3) 供应商“激励”策略和零售商“偏好利他”策略对供应链成员是有益的。2种需求条件下,供应链长期均衡策略均为零售商采取“偏好利他”策略,供应商采取“激励”策略,此时供应商利润达到最高,零售商效用达到最大,双方更愿意保持稳定的合作关系。
本文的贡献在于考虑供应链的动态演化特征,将零售商利他偏好与信息非对称同时引入到供应链中,采用演化博弈理论分析零售商利他偏好对零供决策的影响,并对线性需求函数和非线性需求函数下零供双方的均衡策略进行对比分析。最后运用Matlab仿真分析供应链的演化稳定策略,补充和完善了利他偏好下的供应链批发价格契约研究。
本文的不足如下。1) 仅考虑了零售商具有利他偏好的情形,未来研究可以考虑零供双方均具有利他偏好的情况,并采用演化博弈理论进行分析,验证结论的普遍性;2) 仅考虑了线性需求条件下和非线性需求条件下零供双方博弈的情况,未来研究可以考虑在随机需求函数条件下采用演化博弈理论进行分析,以得到更符合实际的结论。
-
表 1 线性需求下博弈双方的支付矩阵
Table 1 The payoff matrix of both sides under linear demand
供应商 零售商 偏好利他({y^{\rm l}}) 不偏好利他(1 - {y^{\rm l}}) 激励({x^{\rm l}}) \pi _{{\rm{s}}4}^{{\rm l}*} = \dfrac{ { { {({a^{\rm l} } - {b^{\rm l} }c)}^2} } }{ {8{b^{\rm l} }(1 - \beta )} } \pi _{{\rm s}3}^{{\rm l}*} = \dfrac{{{{({a^{\rm l}} - {b^{\rm l}}c)}^2}(1 - 2\beta )}}{{8{b^{\rm l}}{{(1 - \beta )}^2}}} u_{{\rm r}4}^{{\rm l}*} = \dfrac{{{{({a^{\rm l}} - {b^{\rm l}}c)}^2}}}{{16{b^{\rm l}}}} u_{{\rm r}3}^{{\rm l}*} = \dfrac{{{{({a^{\rm l}} - {b^{\rm l}}c)}^2}{{(1 - 2\beta )}^2}}}{{16{b^{\rm l}}{{(1 - \beta )}^2}}} 不激励(1 - {x^{\rm l}}) \pi _{{\rm s}2}^{{\rm l}*} = \dfrac{{{{({a^{\rm l}} - {b^{\rm l}}c)}^2}(1 + \beta )}}{{8{b^{\rm l}}}} \pi _{{\rm s}1}^{{\rm l}*} = \dfrac{{{{({a^{\rm l}} - {b^{\rm l}}c)}^2}}}{{8{b^{\rm l}}}} u_{{\rm r}2}^{{\rm l}*} = \dfrac{{{{({a^{\rm l}} - {b^{\rm l}}c)}^2}{{(1 + \beta )}^2}}}{{16{b^{\rm l}}}} u_{{\rm r}1}^{{\rm l}*} = \dfrac{{{{({a^{\rm l}} - {b^{\rm l}}c)}^2}}}{{16{b^{\rm l}}}} 表 2 非线性需求下博弈双方的支付矩阵
Table 2 The payoff matrix of both sides under nonlinear demand
供应商 零售商 偏好利他({y^{\rm n}}) 不偏好利他(1 - {y^{\rm n}}) 激励({x^{\rm n}}) \pi _{{\rm s}4}^{{\rm n}*} = \dfrac{{a^{\rm n}}{{\rm e}^{ - (2 + {b^{\rm n}}c)}}}{{{b^{\rm n}}(1 - \beta )}} \pi _{{\rm s}3}^{{\rm n}*} = \dfrac{{a^{\rm n}}{{\rm e}^{ - \left({b^{\rm n}}c + \frac{{2 - \beta }}{{1 - \beta }}\right)}}}{{{b^{\rm n}}(1 - \beta )}} {\rm{ }}u_{{\rm r}4}^{{\rm n}*} = \dfrac{{a^{\rm n}}{{\rm e}^{ - (2 + {b^{\rm n}}c)}}}{{{b^{\rm n}}}} {\rm{ }}u_{{\rm r}3}^{{\rm n}*} = \dfrac{{a^{\rm n}}{{\rm e}^{ - \left({b^{\rm n}}c + \frac{{2 - \beta }}{{1 - \beta }}\right)}}}{{{b^{\rm n}}}} 不激励(1 - {x^{\rm n}}) \pi _{{\rm s}2}^{{\rm n}*} = \dfrac{{a^{\rm n}}{{\rm e}^{ - (2 + {b^{\rm n}}c - \beta )}}}{{{b^{\rm n}}}} \pi _{{\rm s}1}^{{\rm n}*} = \dfrac{{a^{\rm n}}{{\rm e}^{ - (2 + {b^{\rm n}}c)}}}{{{b^{\rm n}}}} u_{{\rm r}2}^{{\rm n}*} = \dfrac{{a^{\rm n}}{{\rm e}^{ - (2 + {b^{\rm n}}c - \beta )}}}{{{b^{\rm n}}}} u_{{\rm r}1}^{{\rm n}*} = \dfrac{{a^{\rm n}}{{\rm e}^{ - (2 + {b^{\rm n}}c)}}}{{{b^{\rm n}}}} 表 3 均衡点的局部均衡稳定性分析1)
Table 3 The stable analysis of each local equilibrium point
均衡点 {\rm{Det}}({\boldsymbol{J}}) {\rm{Tr}}({\boldsymbol{J}}) 稳定性 {x^{\rm l}} = 0, {y^{\rm l}} = 0 - fjh - - f + jh A,+ 鞍点 B, 0 C, − {x^{\rm l}} = 1, {y^{\rm l}} = 0 fj(h - {\beta ^4}) + f + j(h - {\beta ^4}) + 不稳
定点{x^{\rm l}} = 0, {y^{\rm l}} = 1 - fmjh - fm - jh - 鞍点 {x^{\rm l}} = 1, {y^{\rm l}} = 1 fmj(h - {\beta ^4}) + - fm - j(h - {\beta ^4}) - {\rm{ESS}} 1) A: 0 \leqslant \beta < \sqrt 2 - 1; B: \beta = \sqrt 2 - 1; C: \sqrt 2 - 1 < \beta \leqslant \dfrac{1}{2} 表 4 均衡点的局部均衡稳定性分析
Table 4 The stable analysis of each local equilibrium point
均衡点 {\rm{Det}}({\boldsymbol{J}}) {\rm{Tr}}({\boldsymbol{J}}) 稳定性 x = 0, y = 0 {g^2}ksr - g(ks + r) + 鞍点 x = 1, y = 0 - {g^2}kvr + g(kv - r) + 不稳定点 x = 0, y = 1 - {g^2}ksz - g( - ks + z) - 鞍点 x = 1, y = 1 {g^2}kvz + - g(kv + z) - {\rm{ESS}} x = N, y = M - {g^2}k\dfrac{{svrz}}{{(s - v)(r - z)}} - 0 0 鞍点 -
[1] 孙玉玲, 袁晓杰, 石岿然. 基于利他偏好的鲜活农产品供应链决策研究[J]. 系统工程理论与实践, 2017, 37(5): 1243-1253. DOI: 10.12011/1000-6788(2017)05-1243-11 SUN Yuling, YUAN Xiaojie, SHI Kuiran. Research on decision of supply chain of fresh agricultural product based on altruism preference[J]. Systems Engineering—Theory & Practice, 2017, 37(5): 1243-1253. DOI: 10.12011/1000-6788(2017)05-1243-11
[2] 李保勇, 马德青, 戴更新. 基于质量识别与成员利他的农产品供应链动态策略研究[J]. 工业工程与管理, 2020, 25(4): 95-104. LI Baoyong, MA Deqing, DAI Gengxin. Research on dynamic strategies of agricultural product supply chain based on quality identification and member altruism[J]. Industrial Engineering and Management, 2020, 25(4): 95-104.
[3] 吴正祥, 李宝库, 赵博. 零售商利他偏好对品牌竞争与渠道竞争共存型供应链决策的影响[J]. 软科学, 2017, 31(11): 110-112. WU Zhengxiang, LI Baoku, ZHAO Bo. Imapct of retailer's altruistic preference on strategies under both brand and channel competition[J]. Soft Science, 2017, 31(11): 110-112.
[4] 徐翔斌, 李恒, 史峰. 多重社会偏好下供应链协调研究[J]. 系统管理学报, 2017, 26(1): 154-162. XU Xiangbin, LI Heng, SHI Feng. Supply chain coordination under multiple social preferences[J]. Journal of Systems & Management, 2017, 26(1): 154-162.
[5] 牛占文, 郁艳青, 何龙飞. 批发价格契约下考虑公平关切的供应链协调及契约设计[J]. 工业工程, 2014, 17(4): 63-69. DOI: 10.3969/j.issn.1007-7375.2014.04.011 NIU Zhanwen, YU Yanqing, HE Longfei. Effects of fairness concerns on supply chain coordination and contract design[J]. Industrial Engineering Journal, 2014, 17(4): 63-69. DOI: 10.3969/j.issn.1007-7375.2014.04.011
[6] GU S, GUO H, SU Y. Research on supply chain coordination and profit allocation based on altruistic principal under bilateral asymmetric information[J]. Discrete Dynamics in Nature and Society, 2018: 1-15.
[7] GE Z H, ZHANG Z K, LYV L Y, et al. How altruism works: an evolutionary model of supply networks[J]. Physica A: Statistical Mechanics & Its Applications, 2012, 391(3): 647-655.
[8] 骆正清, 刘思绮. 不同博弈结构下基于利他偏好的双渠道供应链价格决策分析[J]. 工业技术经济, 2019, 38(3): 28-35. DOI: 10.3969/j.issn.1004-910X.2019.03.004 LUO Zhengqing, LIU Siqi. Analysis on price decision of dual channel supply chain with altruism in different game structures[J]. Journal of Industrial Technological Economics, 2019, 38(3): 28-35. DOI: 10.3969/j.issn.1004-910X.2019.03.004
[9] SHI K, JIANG F, OUYANG Q. Altruism and pricing strategy in dual-channel supply chains[J]. American Journal of Operations Research, 2013, 3(4): 402-412. DOI: 10.4236/ajor.2013.34038
[10] 骆正清, 董永杰. 利他偏好下双渠道供应链定价决策研究[J]. 工业技术经济, 2018, 37(2): 91-98. DOI: 10.3969/j.issn.1004-910X.2018.02.011 LUO Zhengqing, DONG Yongjie. Study on pricing decision of dual-channel supply chain under altruistic preferences[J]. Journal of Industrial Technological Economics, 2018, 37(2): 91-98. DOI: 10.3969/j.issn.1004-910X.2018.02.011
[11] 张焕勇, 梁瑞, 刘燃. 不同主导权力下考虑利他偏好的闭环供应链决策分析[J]. 生态经济, 2019, 35(8): 75-82. ZHANG Huanyong, LIANG Rui, LIU Ran. Decision-making analysis of closed-loop supply chain considering altruistic preferences under different channel powers[J]. Ecological Economy, 2019, 35(8): 75-82.
[12] 王永龙, 蹇明, 宋璇, 等. 考虑零售商具有决策偏差的供应链努力行为研究[J]. 系统科学学报, 2018, 26(3): 81-86. WANG Yonglong, JIAN Ming, SONG Xuan, et al. Analysis on effort of supply chain considering retailer’s decision bias[J]. Journal of Systems Science, 2018, 26(3): 81-86.
[13] 王志宏, 张怡, 郭剑锋, 等. 双重信息非对称下供应链的商业信用契约[J]. 中国管理科学, 2017, 25(9): 148-158. WANG Zhihong, ZHANG Yi, GUO Jianfeng, et al. Trade credit contract in a supply chain under dual asymmetric information[J]. Chinese Journal of Management Science, 2017, 25(9): 148-158.
[14] LUO J, ZHANG Q. Trade credit: a new-mechanism to coordinate supply chain[J]. Operations Research Letters, 2012, 40(5): 378-384. DOI: 10.1016/j.orl.2012.04.008
[15] 王志宏, 洪余芬. 非对称信息下供应链的商业信用激励[J]. 运筹与管理, 2016, 25(4): 134-141. WANG Zhihong, HONG Yufen. Incentive mechanism based on trade credit in a supply chain under asymmetric information[J]. Operations Research and Management Science, 2016, 25(4): 134-141.
[16] 蔡东, 胡七丹, 郭春香. 碳交易下供应链中的技术创新激励合约设计[J]. 工业工程, 2019, 22(5): 133-140. CAI Dong, HU Qidan, GUO Chunxiang. Design of incentive contracts for technological innovation in supply chain under carbon trading[J]. Industrial Engineering Journal, 2019, 22(5): 133-140.
[17] 金亮, 张旭梅, 李诗杨. 不对称信息下线下到线上O2O供应链佣金契约设计[J]. 管理学报, 2017, 14(6): 908-915. DOI: 10.3969/j.issn.1672-884x.2017.06.014 JIN Liang, ZHANG Xumei, LI Shiyang. Commission contract design in offline to online (O2O) supply chain under asymmetric information[J]. Chinese Journal of Management, 2017, 14(6): 908-915. DOI: 10.3969/j.issn.1672-884x.2017.06.014
[18] BASSI M, PAGNOZZI M, PICCOLO S. Optimal contracting with altruism and reciprocity[J]. Research in Economics, 2014, 68: 27-38. DOI: 10.1016/j.rie.2013.12.001
[19] 石岿然, 蒋凤, 孙玉玲. 利他偏好对双渠道供应链成员企业的策略影响研究[J]. 运筹与管理, 2018, 27(9): 66-72. SHI Kuiran, JIANG Feng, SUN Yuling. Effect of altruism on members′ strategies in dual-channel supply chain[J]. Operations Research and Management Science, 2018, 27(9): 66-72.
[20] XU F, WANG H. Competitive–cooperative strategy based on altruistic behavior for dual-channel supply chain[J]. Sustainability, 2018, 10(6): 2103_1-2103_15. DOI: 10.3390/su10062103
[21] 覃燕红, 艾兴政, 宋寒. 利他偏好下基于批发价格契约的供应链协调[J]. 工业工程与管理, 2015, 20(2): 109-121. DOI: 10.3969/j.issn.1007-5429.2015.02.017 QIN Yanhong, AI Xingzheng, SONG Han. Supply chain coordination based on wholesale price contract under altruism[J]. Industrial Engineering and Management, 2015, 20(2): 109-121. DOI: 10.3969/j.issn.1007-5429.2015.02.017
[22] 刘婷婷, 徐庆. 非对称生产成本变动信息下零售商双渠道的最优契约设计[J]. 工业工程, 2017, 20(1): 36-43,58. DOI: 10.3969/j.issn.1007-7375.e16-1111 LIU Tingting, XU Qing. The optimal contract design with asymmetric production cost disruption information in a dual-channel model of retailer[J]. Industrial Engineering Journal, 2017, 20(1): 36-43,58. DOI: 10.3969/j.issn.1007-7375.e16-1111
[23] 周建亨, 赵瑞娟. 考虑引入渠道竞争的双渠道信号传递策略[J]. 系统工程理论与实践, 2018, 38(2): 414-428. DOI: 10.12011/1000-6788(2018)02-0414-15 ZHOU Jianheng, ZHAO Ruijuan. Dual-channel signaling strategy with channel competition[J]. Systems Engineering—Theory & Practice, 2018, 38(2): 414-428. DOI: 10.12011/1000-6788(2018)02-0414-15
[24] 潘旭, 李军, 刘悦秋. 基于委托代理框架的“公司+农户”模式激励研究[J]. 工业工程, 2018, 21(1): 59-66. DOI: 10.3969/j.issn.1007-7375.e17-2285 PAN Xu, LI Jun, LIU Yueqiu. A research on incentive “company + farmer” mode based on principal agent framework[J]. Industrial Engineering Journal, 2018, 21(1): 59-66. DOI: 10.3969/j.issn.1007-7375.e17-2285
[25] 王伟冬, 李小燕. 考虑竞争和信息不对称的低碳供应链协调 策略研究[J]. 工业工程与管理, 2020(3): 27-33. WANG Weidong, LI Xiaoyan. Study on the coordination of low-carbon supply chain considering the competition and information asymmetry[J]. Industrial Engineering and Management, 2020(3): 27-33.
[26] CAGINALP G, HO S J. Does competition inhibit fairness and altruism?[J]. Economic Modelling, 2018, 72: 54-64.
[27] FRIEDMAN D. Evolutionary game in economics[J]. Econometrica, 1991, 59(3): 637-666. DOI: 10.2307/2938222
-
期刊类型引用(3)
1. 王国义,牛丹婷,郭文静,于晓辉. 基于电商平台农产品供应链三方博弈分析. 中国农业文摘-农业工程. 2024(06): 13-20 .  百度学术
百度学术
2. 武柏宇,仲伟俊,梅姝娥. 双重依赖下分包商利他偏好真的有利于公共产品技术创新吗?. 中国管理科学. 2023(02): 182-194 .  百度学术
百度学术
3. 邢青松,钟婉秋,彭鑫,邓富民. 碳减排与超限禁入外部效应下轻量化商用车供应链演化博弈分析. 工业工程. 2023(03): 18-28 .  本站查看
本站查看
其他类型引用(4)



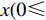
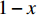
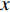
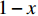
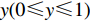
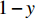
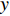
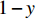
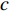
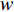
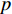
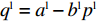
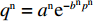
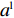
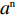
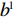
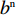
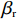
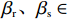
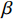
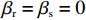
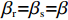
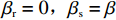
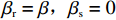
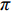
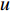
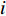
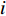
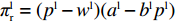
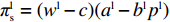
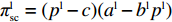

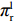
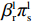
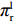
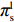
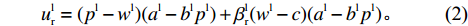
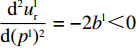
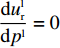
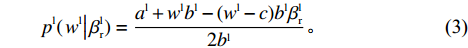
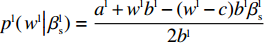
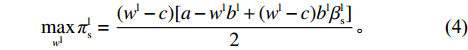
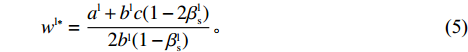
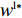
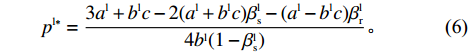
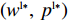
 下载:
下载: