A Research on Supply Chain Coordination of Fresh Agricultural Products Considering Bilateral Fresh-keeping Efforts under Fairness Concern
-
摘要:
针对供应商主导的生鲜农产品供应链,建立Stackelberg博弈模型;在考虑供应商、零售商双边保鲜努力水平影响生鲜农产品新鲜度和市场需求的情况下,分析零售商公平偏好对生鲜农产品供应链双边保鲜努力水平和供应链协调性的影响;采用委托代理模型对“批发价格 + 转移支付”的组合契约协调机制进行研究,旨在增加供应链整体利益及其稳定性,更好地协调成员之间的利益。研究表明,无论是否考虑零售商公平偏好,批发价格契约均无法实现生鲜农产品供应链协调,且零售商公平偏好会进一步降低双边保鲜努力水平、使供应链偏离最优。最后基于“批发价格 + 转移支付”的组合契约不仅能使双边保鲜努力水平达到集中决策下最优,实现生鲜农产品供应链协调,还能实现供应链成员利润的帕累托改进。
Abstract:In the supply chain of fresh agricultural products dominated by the supplier, considering the level of fresh-keeping efforts of both the supplier and the retailer and the efforts will affect the freshness and market demand of fresh agricultural products, a Stackelberg game model was set to analyze the impact of retailer's fairness concern on the bilateral fresh-keeping effort level and supply chain coordination. The principal-agent model was applied to design a combined contract based on "wholesale price + transfer payment" in order to increase the overall benefit and stability of the supply chain and better coordinate the interest of both the supplier and the retailer. Research shows that the wholesale price contract cannot coordinate the supply chain of fresh agricultural product whether the retailer is concerned about fairness, and the retailer's fairness concern further reduces the level of bilateral fresh-keeping efforts and further deviates the supply chain from optimal status. Finally, the combined contract based on "wholesale price + transfer payment" can not only achieve the optimal solution of bilateral fresh-keeping efforts and the coordination of fresh agricultural products supply chain, but also achieve Pareto profit improvement of each supply chain members.
-
生鲜农产品具有高易腐性、流通难度大、保鲜成本高等特点,造成其流通过程中保鲜问题备受社会关注。生鲜农产品供应链的保鲜努力水平通过影响生鲜农产品的新鲜度进而影响生鲜农产品的有效供给。为满足消费者对生鲜农产品的高品质要求,供应链成员会通过提高保鲜努力水平如增加保鲜设备、技术投入来提高生鲜农产品新鲜度。例如湖北武陵山城郊蔬菜基地为提高蔬菜供应新鲜度已建成冷库224个、总库容达到4.8 万m2,其下游合作零售商永辉超市对生鲜设备(如冰柜、喷雾保湿冷柜、冰台和冷藏展示台等)投入占超市整体投入的55%~70%,供应链成员的共同保鲜努力极大提高了蔬菜的新鲜度和品质[1]。在生鲜农产品供应链运作中,一方面由于零售商处于生鲜农产品供应链末端、面临较大的保鲜压力和较多的收益风险;另一方面生鲜农产品供应商在供应链中处于主导地位、得到较多的利益分配,零售商会关注供应链利益分配的公平性,甚至做出投机行为,这会影响生鲜农产品的品质,损害整个生鲜农产品供应链的利益[2]。因此,在生鲜农产品供应链中考虑零售商的公平偏好行为,研究零售商公平偏好行为对生鲜农产品供应链双边保鲜努力水平优化和供应链协调的影响具有重要意义。
国内外很多学者对生鲜农产品供应链的保鲜努力优化和供应链协调进行了研究。Cai等[3]在假设供应商负责运输、分销商负责农产品保鲜和定价的条件下设计促进分销商提高保鲜努力水平和供应链协调的批发价格和成本分担的组合契约。Lee等[4]在假设生鲜农产品库存影响需求的情况下构建变质库存模型并计算了零售商最优保鲜努力水平。王磊等[5]考虑消费者对生鲜品消费效用的情况下设计“批发价格 + 保鲜成本分担”契约促进供应商提高保鲜努力水平的激励机制。Seo等[6]采用实证研究分析分销商保鲜努力和投入对生鲜农产品生鲜度的影响。姚冠新等[7]在假设物流服务商负责生鲜农产品保鲜且其保鲜努力信息非对称条件下,运用委托代理理论设计基于线性分成契约的有效保鲜激励机制。曹裕等[8]证明生鲜农产品供应链总利润随终端零售商保鲜努力水平严格递增,并设计激励机制减少供应商在保鲜投入的搭便车行为,进一步提高生鲜产品的品质。曹武军等[9]发现两部收费制契约不仅可以协调生鲜农产品供应链,还能稳定供应链成员之间的合作关系。
事实上,供应链成员不总是完全理性的,决策时不仅仅以利润最大作为准则。大量博弈理论和实验研究证明决策者在决策时会受到公平偏好的影响,表现为决策者会将自身收益与参考者收益进行比较,当他感觉收益分配不公平时,会丧失理性采取报复、惩罚对方的行为,哪怕牺牲自身收益。继Cui等[10]和Caliskan等[11]分别在线性需求和非线性需求条件下证明考虑公平偏好能够实现批发价格契约协调供应链之后,学者纷纷研究公平偏好对供应链相关决策和契约协调性的影响,得到更符合实践供应链运作的理论研究结论[12-18]。由于生鲜农产品供应链备受实践和理论关注,越来越多的学者开始考虑公平偏好对生鲜农产品供应链运作的影响,如曹武军等[19]研究供应商的公平偏好行为对生鲜产品新鲜度和供应链批发价格契约协调性的影响。洪美娜等[20]考虑零售商的公平偏好,并发现批发价契约无法协调考虑公平偏好的鲜活农产品供应链,但订购量、供应链成员的利润均随着公平偏好程度的上升而减少。张旭等[21-22]建立供应商主导的二级生鲜农产品供应链模型,证明零售商公平偏好越强、供应商让渡收益越多,同时他提出一种改进的旁支付自动执行契约实现供应链协调并帕累托改进双方收益。熊峰等[23]研究供应商公平偏好对零售商生鲜农产品质量投入与定价的影响。
通过以往文献回顾发现,目前生鲜农产品供应链已经成为研究焦点和热点,但是现有研究还存在如下不足:1) 虽然已经有文献考虑生鲜农产品的损耗,研究保鲜努力对提高生鲜农产品品质和供应链协调的重要性,但是这些文献基本都假设供应链决策者都是完全理性的;2) 虽然已经有部分文献将公平偏好纳入生鲜农产品供应链中,分析公平偏好对生鲜农产品相关决策和协调性的影响,但现有文献主要集中于研究公平偏好对供应链某个成员的单边保鲜努力水平优化和激励机制的影响,忽略了供应链中零供双边保鲜努力决策和优化问题。针对这2个问题并结合生鲜农产品新鲜度随时间衰减的特征,在考虑供应商、零售商双边保鲜努力水平影响生鲜农产品新鲜度和市场需求的情况下,分析零售商公平偏好对生鲜农产品供应链双边保鲜努力水平和供应链协调性的影响,拟设计一种协调机制协调具有公平偏好的生鲜农产品供应链,提高双边保鲜努力水平,同时实现双方决策目标的Parato改进。
1. 模型描述和基本假设
研究由单一供应商和单一零售商组成的单周期生鲜农产品供应链,其中供应商处于主导地位、零售商处于跟随地位,且供应商和零售商通过双边保鲜努力来保证生鲜农产品的新鲜度,满足消费者对生鲜度的要求。同时,由于供应商为了增强自身的竞争力和保证农产品运达市场的有效数量和新鲜度,供应商负责从收购农产品到批发产品给零售商过程中的冷藏运输、保鲜包装、送货上门和上架整理等服务,为了便于分析,将这些过程发生的成本归入供应商收购价格
c0 中。供应商和零售商之间构成Stackelberg博弈:首先由供应商基于收购价格c0 决策自身保鲜努力es 和批发价格w ;然后零售商决策生鲜农产品订购量q 和自身保鲜努力er 。本文的具体假设如下。假设1 生鲜农产品新鲜度
θ 是时间t 的加速递减函数,即θ′(t)<0 、θ″(t)<0 ,以η0 表示生鲜农产品经过销售周期T 后的衰减极值,且η0∈(0,1) ;es 、er 分别表示供应商、零售商的保鲜努力水平,且es 、er⩾ ;{k_{\rm s}} 、{k_{\rm r}} 分别表示供应商、零售商保鲜努力对保鲜效果的影响。为简化计算,假设双方保鲜努力对新鲜度影响相同且满足{k_{\rm s}} = {k_{\rm r}} = 1 。于是生鲜农产品新鲜度表示为\theta (t) = {e_{\rm s}} + {e_{\rm r}} - {\eta _0}\dfrac{{{t^2}}}{{{T^2}}} 。假设2 供应商和零售商因投入保鲜努力而产生的成本函数满足
{c'_{\rm s}} ({e_{\rm s}}) {\text{>}} 0 、{c''_{\rm s}}({e_{\rm s}}) {\text{>}} 0 ,{c'_{\rm r}} ({e_{\rm r}}) {\text{>}} 0 、{c''_{\rm r}}({e_{\rm r}}) {\text{>}} 0 ,即随着供应商、零售商保鲜努力水平增加,保鲜努力成本增加且增加速度加快,于是供应商和零售商的保鲜努力成本函数分别为{c_{\rm s}} = \dfrac{1}{2}e_{\rm s}^2 ,{c_{\rm r}} = \dfrac{1}{2}e_{\rm r}^2 。假设3 生鲜农产品市场需求主要受价格和新鲜度影响,同张旭等[22]的研究,生鲜农产品需求表示为
d(p,t) = a - \alpha p + \beta \theta (t) ,其中,a 表示生鲜农产品的市场需求规模且a {\text{>}} 0 ;\alpha 和\beta 分别表示市场需求对价格和新鲜度的敏感系数且\alpha 、\;\beta {\text{>}} 0 。为保证任何情况下零售商订购量为正,设T{\beta ^{\rm{2}}} {\text{<}} \alpha {\text{<}} 2T{\beta ^{\rm{2}}} 。假设4 生鲜农产品在运输途中的变质只表现为因表面蒙尘或水分缺失而造成的新鲜度降低,不考虑运输途中由于变质引起的数量减少。
文中以下标s、r和sc分别表示供应商、零售商和供应链系统,以上标c表示集中决策情形,以n、f分别表示零售商公平中性、公平偏好下仅采用批发价格契约情形,以nz、fz分别表示零售商公平中性、公平偏好下引入转移支付F的情形,以上标*代表最优。
2. 集中决策
集中决策模式下,供应商和零售商合作作为一个整体,以生鲜供应链系统利润最优来决策双边保鲜努力水平和订购量。由于不考虑销售剩余和缺货的情况,因此零售商的生鲜品订购量即为一个销售周期内的销售量。
\begin{split} & \qquad q = \int_0^T {\left[a - \alpha p + \beta ({e_{\rm s}} + {e_{\rm r}} - {\eta _0}\dfrac{{{t^2}}}{{{T^2}}})\right]} {\rm{d}}t = \left[\dfrac{M}{3} -\alpha p +\right.\\ & \left. \beta ({e_{\rm s}} + {e_{\rm r}})\right]T{\text{。}} \end{split} (1) 其中,
M = 3a - \beta {\eta _0} 。由于零售商订购量始终非负,即当{e_{\rm s}} = 0 、{e_{\rm r}} = 0 时,仍然有q {\text{>}} 0 ,即M - 3\alpha {c_0} {\text{>}} 0 。由式(1)可得
\qquad p = \dfrac{M}{{3\alpha }} + \dfrac{{\beta ({e_{\rm s}} + {e_{\rm r}})}}{\alpha } - \dfrac{q}{{\alpha T}}{\text{。}} (2) 于是集中决策下供应链系统利润函数为
\qquad \pi\; _{\rm sc}^{\rm c} = \left[\dfrac{M}{{3\alpha }} + \dfrac{{\beta ({e_{\rm s}} + {e_{\rm r}})}}{\alpha } - \dfrac{q}{{\alpha T}} - {c_0}\right]q - \dfrac{1}{2}e_{\rm s}^2 - \dfrac{1}{2}e_{\rm r}^2{\text{。}} (3) 可以计算
\pi \,_{\rm sc}^{\rm c} 的Hessian矩阵为\qquad {{\boldsymbol{H}}_1} = \left[ {\begin{array}{*{20}{c}} \dfrac{ - 2}{\alpha T}&\dfrac{\beta} {\alpha }&\dfrac{\beta} {\alpha } \\ \dfrac{\beta} {\alpha }&{ - 1}&0 \\ \dfrac{\beta} {\alpha }&0&{ - 1} \end{array}} \right]{\text{。}} 结合
T{\beta ^{\rm{2}}} {\text{<}} \alpha {\text{<}} 2T{\beta ^{\rm{2}}} 可知,H_1^1 = - \dfrac{2}{{\alpha T}} {\text{<}} 0 ,H_1^2 = \dfrac{{2\alpha - T{\beta ^2}}}{{{\alpha ^2}T}} {\text{>}} 0 ,H_1^3 = \dfrac{{2T{\beta ^2} - 2\alpha }}{{{\alpha ^2}T}} {\text{<}} 0 ,即矩阵{{\boldsymbol{H}}_1} 为负定,因此\pi \,_{\rm sc}^{\rm c} 为严格凹函数,存在唯一最优系统订购量和零、供双方保鲜努力水平使\pi \,_{\rm sc}^{\rm c} 达到最大值。同时令\dfrac{{\partial \pi\; _{\rm sc}^{\rm c}}}{{\partial q}} = 0 、\dfrac{{\partial \pi \; _{\rm sc}^{\rm c}}}{{\partial {e_{\rm s}}}} = 0 和\dfrac{{\partial \pi \; _{\rm sc}^{\rm c}}}{{\partial {e_{\rm r}}}} = 0 ,可得集中决策下供应链系统最优订购量{q^{\rm c * }} 、零售商最优保鲜努力水平e_{\rm r}^{\rm c * } 以及供应商最优保鲜努力水平e_{\rm s}^{\rm c * } 分别为\qquad {q^{\rm c * }} = \dfrac{{\alpha T(M - 3\alpha {c_0})}}{{6(\alpha - T{\beta ^2})}}; (4) \qquad e_{\rm r}^{\rm c * } = \dfrac{{\beta T(M - 3\alpha {c_0})}}{{6(\alpha - T{\beta ^2})}}; (5) \qquad e_{\rm s}^{\rm c * } = \dfrac{{\beta T(M - 3\alpha {c_0})}}{{6(\alpha - T{\beta ^2})}}{\text{。}} (6) 将式(4) ~ (6)代入式(3)可计算集中决策下供应链系统最优利润为
\qquad \pi \,_{\rm sc}^{\rm c * } = \dfrac{{T{{(M - 3\alpha {c_0})}^2}}}{{36(\alpha - T{\beta ^2})}}{\text{。}} (7) 3. 基于批发价格契约的分散决策模型
3.1 零售商公平中性情形
分散决策下,供应商与零售商进行Stackelberg博弈,首先处于主导地位的供应商根据利润最大化决策生鲜农产品的批发价格
w 和保鲜努力水平{e_{\rm s}} ,然后公平中性的零售商根据w 和{e_{\rm s}} 以自身利润最大化决策订购量q 和保鲜努力水平{e_{\rm r}} 。由需求函数可得供应商和零售商利润函数分别为\qquad \pi \,_{\rm s}^{\rm n} = (w - {c_0})q - \dfrac{1}{2}e_{\rm s}^2; (8) \qquad \pi \,_{\rm r}^{\rm n} = \left[\dfrac{M}{{3\alpha }} + \dfrac{{\beta ({e_{\rm s}} + {e_{\rm r}})}}{\alpha } - \dfrac{q}{{\alpha T}} - w \right]q - \dfrac{1}{2}e_{\rm r}^2{\text{。}} (9) 采用逆向归纳法求解该Stackelberg博弈,在博弈第2阶段,零售商的决策为
\qquad \mathop {{\rm{max}}}\limits_{q,{e_{\rm r}}} \pi \,_{\rm r}^{\rm n} = \left[\dfrac{M}{{3\alpha }} + \dfrac{{\beta ({e_{\rm s}} + {e_{\rm r}})}}{\alpha } - \dfrac{q}{{\alpha T}} - w\right]q - \dfrac{1}{2}e_{\rm r}^2{\text{。}} (10) 可计算
\pi \,_{\rm r}^{\rm n} 的Hessian矩阵为\qquad {{\boldsymbol{H}}_2} = \left[ {\begin{array}{*{20}{c}} { - \dfrac{2}{{\alpha T}}}&{\dfrac{\beta }{\alpha }} \\ {\dfrac{\beta }{\alpha }}&{ - 1} \end{array}} \right]{\text{。}} 其中,
H_2^1 = - \dfrac{2}{{\alpha T}} {\text{<}} 0 ,H_2^2 = \dfrac{{2\alpha - T{\beta ^2}}}{{{\alpha ^2}T}} 。由T{\beta ^{\rm{2}}} {\text{<}} \alpha {\text{<}} 2T{\beta ^{\rm{2}}} 可得H_{\rm{2}}^{\rm{2}} {\text{>}} 0 ,于是矩阵{{\boldsymbol{H}}_{\rm{2}}} 负定,即零售商决策问题存在唯一最优解。令\dfrac{{\partial \pi \,_{\rm r}^{\rm n}}}{{\partial q}} = 0 ,\dfrac{{\partial \pi \,_{\rm r}^{\rm n}}}{{\partial {e_{\rm r}}}} = 0 ,可得零售商最优订购量{q^{\rm n * }}(w,{e_{\rm s}}) 和保鲜努力水平e_{\rm r}^{\rm n * }(w,{e_{\rm s}}) 分别为\begin{split} \qquad & {q^{\rm n * }}(w,{e_{\rm s}}) = \dfrac{{\alpha T(M - 3\alpha w + 3\beta {e_{\rm s}})}}{{3(2\alpha - T{\beta ^2})}};\\ & e_{\rm r}^{\rm n * }(w,{e_{\rm s}}) = \dfrac{{\beta T(M - 3\alpha w + 3\beta {e_{\rm s}})}}{{3(2\alpha - T{\beta ^2})}}{\text{。}} \end{split} 将
{q^{\rm n * }}(w,{e_{\rm s}}) 代入式(8),可得供应商决策问题为\qquad \mathop {{\rm{max}}}\limits_{w,{e_{\rm s}}} \pi \,_{\rm s}^{\rm n} = (w - {c_0})\dfrac{{\alpha T(M - 3\alpha w + 3\beta {e_{\rm s}})}}{{3(2\alpha - T{\beta ^2})}} - \dfrac{1}{2}e_{\rm s}^2{\text{。}} (11) 同理可以验证
\pi \,_{\rm s}^{\rm n} 的Hessian矩阵\qquad {{\boldsymbol{H}}_3} = \left[ {\begin{array}{*{20}{c}} { - \dfrac{{6{\alpha ^2}T}}{{6\alpha - 3T{\beta ^2}}}}&{\dfrac{{3\alpha T\beta }}{{6\alpha - 3T{\beta ^2}}}} \\ {\dfrac{{3\alpha T\beta }}{{6\alpha - 3T{\beta ^2}}}}&{ - {\rm{1}}} \end{array}} \right] 为负定。通过令
\dfrac{{\partial \pi \,_{\rm s}^{\rm n}}}{{\partial w}} = 0 ,\dfrac{{\partial \pi \,_{\rm s}^{\rm n}}}{{\partial {e_{\rm s}}}} = 0 ,可得供应商最优批发价格{w^{\rm n * }} 和保鲜努力水平e_{\rm s}^{\rm n * } 分别为\qquad {w^{\rm n * }} = \dfrac{{6\alpha {c_0}(\alpha - T{\beta ^2}) + M(2\alpha - T{\beta ^2})}}{{3\alpha (4\alpha - 3T{\beta ^2})}}; (12) \qquad e_{\rm s}^{\rm n * } = \dfrac{{\beta T(M - 3\alpha {c_0})}}{{3(4\alpha - 3T{\beta ^2})}}{\text{。}} (13) 将式(12)、(13)代入式
{q^{\rm n * }}(w,{e_{\rm s}}) 和e_{\rm r}^{\rm n * }(w,{e_{\rm s}}) ,可得零售商最优订购量{q^{\rm n * }} 和保鲜努力水平e_{\rm r}^{\rm n * } 分别为\qquad {q^{\rm n * }} = \dfrac{{\alpha T(M - 3\alpha {c_0})}}{{3(4\alpha - 3T{\beta ^2})}}; (14) \qquad e_{\rm r}^{\rm n * } = \dfrac{{\beta T(M - 3\alpha {c_0})}}{{3(4\alpha - 3T{\beta ^2})}}{\text{。}} (15) 于是分散决策下供应商、零售商以及供应链系统的最优利润分别为
\qquad \pi \,_{\rm s}^{\rm n * } = \dfrac{{T{{(M - 3\alpha {c_0})}^2}}}{{18(4\alpha - 3T{\beta ^2})}}; (16) \qquad\pi \,_{\rm r}^{\rm n * } = \dfrac{{T(2\alpha - T{\beta ^2}){{(M - 3\alpha {c_0})}^2}}}{{18{{(4\alpha - 3T{\beta ^2})}^{\rm{2}}}}}; (17) \qquad \pi \,_{\rm sc}^{\rm n * } = \dfrac{{T(3\alpha - 2T{\beta ^2}){{(M - 3\alpha {c_0})}^2}}}{{9{{(4\alpha - 3T{\beta ^2})}^2}}}{\text{。}} (18) 3.2 零售商公平偏好情形
零售商公平偏好时,根据浦徐进等[16]和覃燕红等[17-18]可得零售商包括自身利润和公平负效用在内的决策目标函数为
\qquad {u_{\rm r}} = {\pi \,_{\rm r}} - \lambda ({\pi \,_{\rm s}} - {\pi \,_{\rm r}}){\text{。}} (19) 其中,
\lambda 表示零售商的公平偏好强度系数。当零售商利润低于供应商时,零售商产生负效用\lambda ({\pi \,_{\rm s}} - {\pi \,_{\rm r}}) ,且{\pi \,_{\rm s}} - {\pi \,_{\rm r}} 的值越大,零售商公平心理负效用越大;当零售商利润高于供应商时,零售商会因为自身获得了供应链总利润中的较大比例而产生自豪正效用,且随两者利润差线性递增。将式(8)、(9)分别代入式(19),可得公平偏好的零售商决策为\begin{split} & \qquad \mathop {{\rm{max}}}\limits_{q,{e_{\rm r}}} u_{\rm r}^{\rm f} = (1 + \lambda )\left[\left(\dfrac{M}{{3\alpha }} + \dfrac{{\beta ({e_{\rm s}} + {e_{\rm r}})}}{\alpha } - \dfrac{q}{{\alpha T}} - w\right)q -\dfrac{1}{2}e_{\rm r}^2\right] -\\ & a\lambda \left[(w - {c_0})q - \dfrac{1}{2}e_{\rm s}^2\right]{\text{。}} \end{split} (20) 同公平中性下的分析可知,
u_{\rm r}^{\rm f} 的Hessian矩阵\qquad {{\boldsymbol{H}}_4} = \left[ {\begin{array}{*{20}{c}} { - \dfrac{{2(1 + \lambda )}}{{\alpha T}}}&{\dfrac{{\beta (1 + \lambda )}}{\alpha }} \\ {\dfrac{{\beta (1 + \lambda )}}{\alpha }}&{ - 1 - \lambda } \end{array}} \right] 为负定。令
\dfrac{{\partial u_{\rm r}^{\rm f}}}{{\partial q}} = 0 和\dfrac{{\partial u_{\rm r}^{\rm f}}}{{\partial {e_{\rm r}}}} = 0 可以得到公平偏好下零售商最优订购量{q^{\rm f * }}(w,{e_{\rm s}}) 和保鲜努力水平e_{\rm r}^{\rm f * }(w,{e_{\rm s}}) 分别为\qquad {q^{\rm f * }}(w,{e_{\rm s}}) = \dfrac{{\alpha T[(\lambda + 1)(M + 3\beta {e_{\rm s}}) - 3\alpha w(2\lambda + 1) + 3\alpha {c_0}\lambda ]}}{{3(\lambda + 1)(2\alpha - T{\beta ^2})}}; \qquad e_{\rm r}^{\rm f * }(w,{e_{\rm s}}) = \dfrac{{\beta T[(\lambda + 1)(M + 3\beta {e_{\rm s}}) - 3\alpha w(2\lambda + 1) + 3\alpha {c_0}\lambda ]}}{{3(\lambda + 1)(2\alpha - T{\beta ^2})}}{\text{。}} 回到博弈第1阶段,当零售商偏好公平时,供应商决策为
\begin{split} & \qquad \mathop {{\rm{max}}}\limits_{w,{e_{\rm s}}} \pi \,_{\rm s}^{\rm f} = (w - {c_0}) \times \\ & \dfrac{{\alpha T[(\lambda + 1)(M + 3\beta {e_{\rm s}}) - 3\alpha w(2\lambda + 1) + 3\alpha {c_0}\lambda ]}}{{3(\lambda + 1)(2\alpha - T{\beta ^2})}} - \dfrac{1}{2}e_{\rm s}^2{\text{。}} \end{split} (21) 可以计算
\pi \,_{\rm s}^{\rm f} 的Hessian矩阵为\begin{split} \qquad {{\boldsymbol{H}}_5} = \left[ {\begin{array}{*{20}{c}} { - \dfrac{{2T{\alpha ^2}(2\lambda + 1)}}{{(\lambda + 1)(2\alpha - T{\beta ^2})}}}&{\dfrac{{T\beta \alpha }}{{2\alpha - T{\beta ^2}}}} \\ {\dfrac{{T\beta \alpha }}{{2\alpha - T{\beta ^2}}}}&{ - 1} \end{array}} \right]{\text{。}} \end{split} 由
H_5^1 = - \dfrac{{2T{\alpha ^2}(2\lambda + 1)}}{{(\lambda + 1)(2\alpha - T{\beta ^2})}} {\text{<}} 0 、H_5^2 = \dfrac{{\lambda T{\alpha ^2}(8\alpha - 5T{\beta ^2}) )}}{{(\lambda + 1){{(2\alpha - T{\beta ^2})}^2}}} +\dfrac{ T{\alpha ^2}(4\alpha - 3T{\beta ^2})}{{(\lambda + 1){{(2\alpha - T{\beta ^2})}^2}}} {\text{>}} 0 ,易知矩阵{{\boldsymbol{H}}_5} 负定。同时令\dfrac{{\partial \pi \,_{\rm s}^{\rm f}}}{{\partial w}} = 0 和\dfrac{{\partial \pi \,_{\rm s}^{\rm f}}}{{\partial {e_{\rm s}}}} = 0 ,可以得到供应商最优批发价格{w^{\rm f * }} 和保鲜努水平e_{\rm s}^{\rm f * } 分别为\begin{split} & \qquad {w^{\rm f * }} =\\ & \dfrac{{6\alpha {c_0}(\alpha - T{\beta ^2}) + M(\lambda + 1)(2\alpha - T{\beta ^2}) + 6\alpha {c_0}\lambda (3\alpha - 2T{\beta ^2})}}{{3\alpha [\lambda (8\alpha - 5T{\beta ^2}) + 4\alpha - 3T{\beta ^2}]}}; \end{split} (22) \qquad e_{\rm s}^{\rm f * } = \dfrac{{\beta T(\lambda + 1)(M - 3\alpha {c_0})}}{{3[\lambda (8\alpha - 5T{\beta ^2}) + 4\alpha - 3T{\beta ^2}]}}{\text{。}} (23) 将式(22)、(23)代入
{q^{\rm f * }}(w,{e_{\rm s}}) 和e_{\rm r}^{\rm f * }(w,{e_{\rm s}}) ,可得零售商最优订购量{q^{\rm f * }} 和最优保鲜努力水平e_{\rm r}^{\rm f * } 分别为\qquad {q^{\rm f * }} = \dfrac{{\alpha T(2\lambda + 1)(M - 3\alpha {c_0})}}{{3[\lambda (8\alpha - 5T{\beta ^2}) + 4\alpha - 3T{\beta ^2}]}}; (24) \qquad e_{\rm r}^{\rm f * } = \dfrac{{\beta T(2\lambda + 1)(M - 3\alpha {c_0})}}{{3[\lambda (8\alpha - 5T{\beta ^2}) + 4\alpha - 3T{\beta ^2}]}}{\text{。}} (25) 零售商公平偏好下供应商最优利润、零售商最优利润和效用以及供应链系统利润分别为
\qquad \pi \,_{\rm s}^{\rm f * } = \dfrac{{T(\lambda + 1){{(M - 3\alpha {c_0})}^2}}}{{18[\lambda (8\alpha - 5T{\beta ^2}) + 4\alpha - 3T{\beta ^2}]}}; (26) \qquad \pi \,_{\rm r}^{\rm f * } = \dfrac{{T(2\alpha - T{\beta ^2}){{(M - 3\alpha {c_0})}^2}\left(4{\lambda ^2} + 3\lambda + \dfrac{{\rm{1}}}{{\rm{2}}}\right)}}{{9{{[\lambda (8\alpha - 5T{\beta ^2}) + 4\alpha - 3T{\beta ^2}]}^2}}}; (27) \begin{split} & \qquad u_{\rm r}^{\rm f * } = \\ & \dfrac{{T(\lambda + 1){{(M - 3\alpha {c_0})}^2}\left[({\lambda ^2} + \lambda )\left(\dfrac{{\rm{8}}}{{\rm{3}}}\alpha - T{\beta ^2}\right) + \dfrac{{\rm{2}}}{{\rm{3}}}\alpha - \dfrac{{\rm{1}}}{{\rm{3}}}T{\beta ^2}\right]}}{{6{{\left[\lambda (8\alpha - 5T{\beta ^2}) + 4\alpha - 3T{\beta ^2}\right]}^2}}}; \end{split} (28) \begin{split} & \qquad \pi \,_{\rm sc}^{\rm f * } =\\ & \dfrac{{T{{(M - 3\alpha {c_0})}^2}[{\lambda ^2}(24\alpha - 13T{\beta ^2}) + \lambda (24\alpha - 14T{\beta ^2}) + (6\alpha - 4T{\beta ^2})]}}{{18{{[\lambda (8\alpha - 5T{\beta ^2}) + 4\alpha - 3T{\beta ^2}]}^2}}}{\text{。}} \end{split} (29) 3.3 集中决策和分散决策的均衡结果分析
将集中决策和零售商公平中性、偏好时分散决策下的最优决策进行比较,可得命题1和性质1。
命题1 ①
{w^{\rm n * }} {\text{>}} w{ ^{\rm f * }} ,{q^{\rm c * }} {\text{>}} {q^{\rm n * }} {\text{>}} {q^{\rm f * }} ,e_{\rm s}^{\rm c * } = e_{\rm r}^{\rm c * } {\text{>}} e_{\rm s}^{\rm n * } = e_{\rm r}^{\rm n * } {\text{>}} e_{\rm r}^{\rm f * } {\text{>}} e_{\rm s}^{\rm f * } ;②\pi \,_{\rm r}^{\rm n * } {\text{<}} \pi \,_{\rm r}^{\rm f * } ,\pi \,_{\rm s}^{\rm n * } {\text{>}} \pi \,_{\rm s}^{\rm f * } ,\pi \,_{\rm sc}^{\rm c * } {\text{>}} \pi \,_{\rm sc}^{\rm n * } {\text{>}} \pi \,_{\rm sc}^{\rm f * } ,\left| {\pi \,_{\rm s}^{\rm n * } -}\right. \left.{ \pi \,_{\rm s}^{\rm f * }} \right| {\text{>}} \left| {\pi \,_{\rm r}^{\rm n * } - }\right. \left. {\pi \,_{\rm r}^{\rm f * }} \right| 。证明
\qquad {w^{\rm n * }} - {w^{\rm f * }} = \dfrac{{2(M - 3\alpha {c_0}){{(2\alpha - T{\beta ^2})}^2}}}{{\left(\dfrac{{\rm{4}}}{{\rm{3}}}\alpha - T{\beta ^2}\right)\alpha [\lambda (72\alpha - 45T{\beta ^2}){\rm{ + 36}}\alpha - {\rm{27}}T{\beta ^2}]}}{\text{。}} 由
T{\beta ^{\rm{2}}} {\text{<}} \alpha {\text{<}} 2T{\beta ^{\rm{2}}} 可得{w^{\rm n * }} {\text{>}} w{ ^{\rm f * }} ;同理,\qquad e_{\rm r}^{\rm c * } - e_{\rm r}^{\rm n * } = \dfrac{{\beta T(M - 3\alpha {c_0})(2\alpha - T{\beta ^2})}}{{18\left(\dfrac{{\rm{4}}}{{\rm{3}}}\alpha - T{\beta ^2}\right)(\alpha - T{\beta ^2})}} {\text{>}} 0; \qquad e_{\rm r}^{\rm n * } - e_{\rm r}^{\rm f * } = \dfrac{{{T^2}{\beta ^3}\lambda (M - 3\alpha {c_0})}}{{3(4\alpha - 3T{\beta ^2})[\lambda (8\alpha - 5T{\beta ^2})\lambda + 4\alpha - 3T{\beta ^2}]}} {\text{>}} 0; \qquad e_{\rm r}^{\rm f * } - e_{\rm s}^{\rm f * } = \dfrac{{\beta T\lambda (M - 3\alpha {c_0})}}{{\lambda (24\alpha - 15T{\beta ^2}) + 12\alpha - 9T{\beta ^2}}} {\text{>}} 0; \qquad {q^{\rm c * }} - {q^{\rm n * }} = \dfrac{{\alpha T(M - 3\alpha {c_0})(2\alpha - T{\beta ^2})}}{{18\left(\dfrac{{\rm{4}}}{{\rm{3}}}\alpha - T{\beta ^2}\right)\left(\alpha - T{\beta ^2}\right)}} {\text{>}} 0; \qquad {q^{\rm n * }} - {q^{\rm f * }} = \dfrac{{\alpha {T^2}{\beta ^2}\lambda (M - 3\alpha {c_0})}}{{3(4\alpha - 3T{\beta ^2})[\lambda (8\alpha - 5T{\beta ^2}) + 4\alpha - 3T{\beta ^2}]}} {\text{>}} 0; \begin{split} \qquad \pi \,_{\rm r}^{\rm n * } - \pi \,_{\rm r}^{\rm f * } = \dfrac{ \lambda T{(M - 3\alpha {c_0})^2}(T{\beta ^2} - 2\alpha )(47{T^2}{\beta ^4}\lambda + 24{T^2}{\beta ^4} - 112T{\beta ^2}\alpha \lambda - 56T{\beta ^2}\alpha + 64{\alpha ^2}\lambda + 32{\alpha ^2}) }{{{{(4\alpha - 3T{\beta ^2})}^2}{{[\lambda (8\alpha - 5T{\beta ^2}) + 4\alpha - 3T{\beta ^2}]}^2}}}{\text{。}} \end{split} 其中,
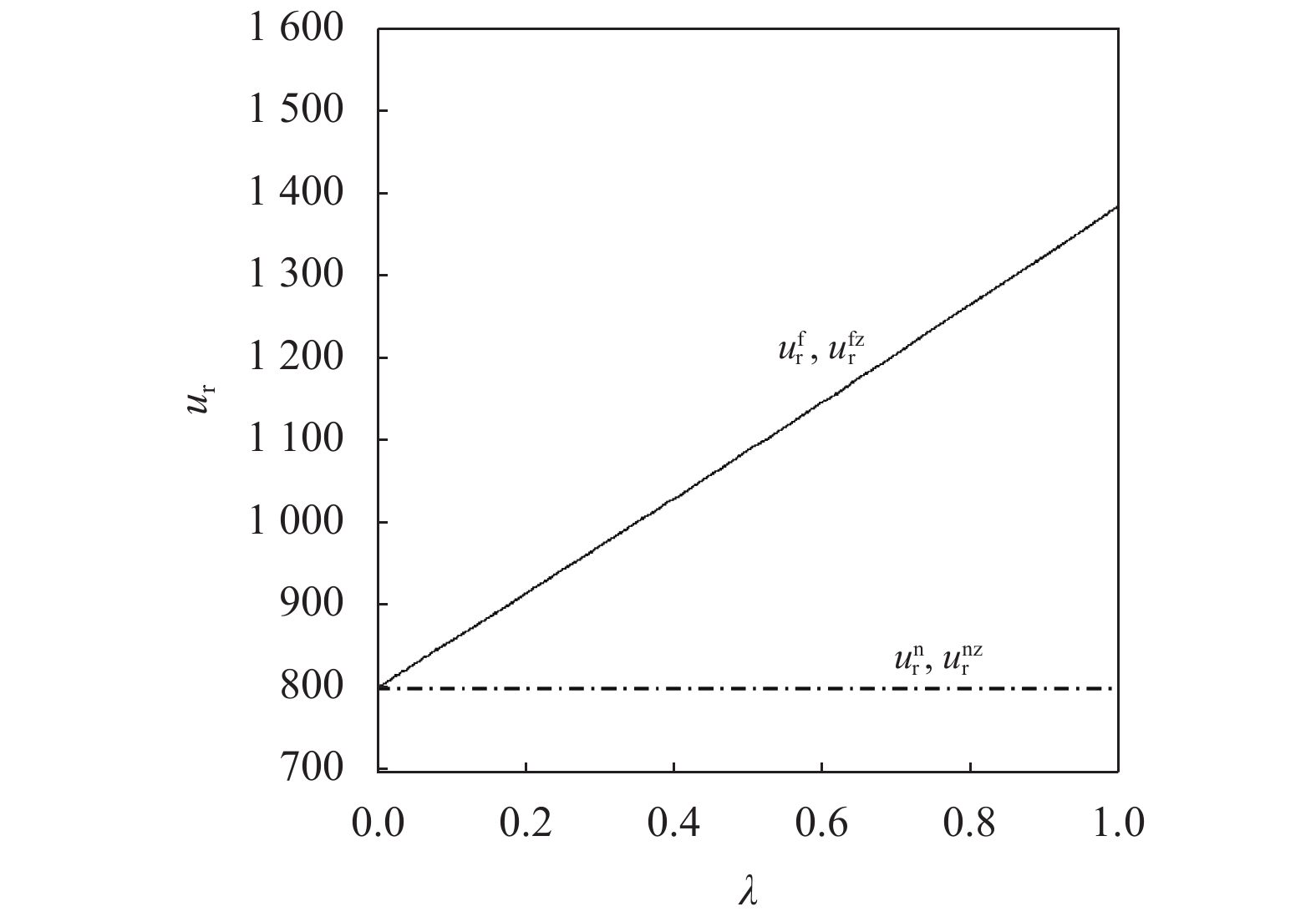
47{T^2}{\beta ^4}\lambda \;+ \;24{T^2}{\beta ^4} \;-\; 112T{\beta ^2}\alpha \lambda \; -\; 56T{\beta ^2}\alpha \;+ 64{\alpha ^2}\lambda +32{\alpha ^2}= {T^2}{\beta ^4}(47\lambda \;+\; 24) - 8\alpha ({\rm{2}}\lambda {\rm{ \;+\; 1}})(7T{\beta ^2} - 4\alpha ){\text{<}} 24({\rm{2}}\lambda+ {\rm{ 1}}){T^2}{\beta ^4} \;-\; 8\alpha ({\rm{2}}\lambda {\rm{ \;+\; 1}})(7T{\beta ^2} - 4\alpha )= {\rm{ 8}}({\rm{2}}\lambda {\rm{ \;+\; 1}})(T{\beta ^2} \; −\alpha )(3T{\beta ^2} - 4\alpha ) 。\begin{split} & \qquad \pi \,_{\rm r}^{\rm n * } - \pi \,_{\rm r}^{\rm f * } {\text{<}}\\ & \dfrac{{8\lambda T{{(M - 3\alpha {c_0})}^2}(2\alpha - T{\beta ^2})(2\lambda + 1)(\alpha - T{\beta ^2})(4\alpha - 3T{\beta ^2})}}{{{{(4\alpha - 3T{\beta ^2})}^2}{{[\lambda (8\alpha - 5T{\beta ^2}) + 4\alpha - 3T{\beta ^2}]}^2}}} {\text{<}} 0; \end{split} \qquad \pi \,_{\rm s}^{\rm n * } - \pi \,_{\rm s}^{\rm f * } = \dfrac{{\lambda T{{(M - 3\alpha {c_0})}^2}(2\alpha - T{\beta ^2})}}{{9(4\alpha - 3T{\beta ^2})[\lambda (8\alpha - 5T{\beta ^2}) + 4\alpha - 3T{\beta ^2}]}} {\text{>}} 0; \qquad \pi \,_{\rm sc}^{\rm c * } - \pi \,_{\rm sc}^{\rm n * } = \dfrac{{T{{(M - 3\alpha {c_0})}^2}{{(2\alpha - T{\beta ^2})}^2}}}{{324{{(\dfrac{4}{3}\alpha - T{\beta ^2})}^2}(\alpha - T{\beta ^2})}} {\text{>}} 0; \begin{split} \qquad \pi \,_{\rm sc}^{\rm n * } - \pi \,_{\rm sc}^{\rm f * } = \dfrac{ {T^2}{\beta ^2}\lambda {(M - 3\alpha {c_0})^2}(2\alpha - T{\beta ^2})[\lambda (24\alpha - 17T{\beta ^2}) + 8\alpha - 6T{\beta ^2}] }{{18{{(4\alpha - 3T{\beta ^2})}^2}{{[\lambda (8\alpha - 5T{\beta ^2}) + 4\alpha - 3T{\beta ^2}]}^2}}} {\text{>}} 0; \end{split} \begin{split} \qquad \left| {\pi \,_{\rm s}^{\rm n * } - \pi \,_{\rm s}^{\rm f * }} \right| - \left| {\pi \,_{\rm r}^{\rm n * } - \pi \,_{\rm r}^{\rm f * }} \right| = \dfrac{ T{(M - 3\alpha {c_0})^2}(2\alpha - T{\beta ^2})\left(\dfrac{{\rm{8}}}{{\rm{7}}}\alpha - T{\beta ^2}\right)[\lambda (112\alpha - 77T{\beta ^2}) + 56\alpha - 42T{\beta ^2}] }{18{(4\alpha - 3T{\beta ^2})^2}[\lambda (8\alpha - 5T{\beta ^2}) + 4\alpha - 3T{\beta ^2}{]^2} } {\text{>}} 0{\text{。}} \end{split} 由命题1①可知,零售商公平偏好下的批发价格低于公平中性情形,零供双边保鲜努力水平和最优订购量变化趋势一致:在公平偏好下最低、公平中性次之、集中决策下最高。集中决策下双边保鲜努力水平相等、零售商公平中性下双边保鲜努力水平相等,但零售商公平偏好下零售商保鲜努力水平高于供应商。由命题1②可知,零售商公平偏好行为会增加零售商利润、减少供应商利润,且供应商利润减少量大于零售商利润增加量,因此,供应链利润在公平偏好下最低、公平中性下次之、集中决策下最高。
命题1说明在供应商主导的生鲜农产品供应链中,零售商公平偏好行为对双方和供应链不利,表现为零售商公平偏好行为导致双边保鲜努力水平、订购量降低从而供应链利润进一步偏离供应链系统最优。虽然零售商公平偏好行为能够通过迫使供应商降低批发价格(
{w^{\rm n * }} {\text{>}} w{ ^{\rm f * }} )、为自身谋取更多的利润(\pi \,_{\rm r}^{\rm n * } {\text{<}} \pi \,_{\rm r}^{\rm f * } ),但是却造成供应商利润更大幅度下降(\left| {\pi \,_{\rm s}^{\rm n * } - \pi \,_{\rm s}^{\rm f * }} \right| {\text{>}} \left| {\pi \,_{\rm r}^{\rm n * } - \pi \,_{\rm r}^{\rm f * }} \right| )从而造成供应链利润降低。因此零售商公平偏好行为对生鲜农产品保鲜和供应链运作是不利的。性质1 ①
\dfrac{{\partial {w^{\rm f * }}}}{{\partial \lambda }} {\text{<}} 0 ,\dfrac{{\partial {q^{\rm f * }}}}{{\partial \lambda }} {\text{<}} 0 ,\dfrac{{\partial e_{\rm s}^{\rm f * }}}{{\partial \lambda }} {\text{<}} 0 ,\dfrac{{\partial e_{\rm r}^{\rm f * }}}{{\partial \lambda }} {\text{<}} 0 ;②
\dfrac{{\partial u_{\rm r}^{\rm f * }}}{{\partial \lambda }} {\text{>}} 0 ,\dfrac{{\partial \pi \,_{\rm s}^{\rm f * }}}{{\partial \lambda }} {\text{<}} 0 ,\dfrac{{\partial \pi \,_{s{\rm{c}}}^{\rm f * }}}{{\partial \lambda }} {\text{<}} 0 ;当T{\beta ^{\rm{2}}} {\text{<}} \alpha {\text{<}} \overline \lambda T{\beta ^{\rm{2}}} 时,\dfrac{{\partial \pi \,_{\rm r}^{\rm f * }}}{{\partial \lambda }} {\text{<}} 0 ;当\overline \lambda T{\beta ^{\rm{2}}} {\text{<}} \alpha {\text{<}} {\rm{2}}T{\beta ^{\rm{2}}} 时,\dfrac{{\partial \pi \,_{\rm r}^{\rm f * }}}{{\partial \lambda }} {\text{>}} 0 。其中,\overline \lambda = \dfrac{{9\lambda + 4}}{{8\lambda + 4}} 。证明
\qquad \dfrac{{\partial {w^{\rm f * }}}}{{\partial \lambda }} = - \dfrac{{2{{(M - 3\alpha {c_0})}^2}{{(2\alpha - T{\beta ^2})}^2}}}{{75\alpha {{\left[\lambda \left(\dfrac{{\rm{8}}}{{\rm{5}}}\alpha - T{\beta ^2}\right) + \dfrac{{\rm{4}}}{{\rm{5}}}\alpha - \dfrac{{\rm{3}}}{{\rm{5}}}T{\beta ^2}\right]}^2}}} {\text{<}} 0; \begin{split} \qquad\dfrac{{\partial {q^{\rm f * }}}}{{\partial \lambda }} = - \dfrac{{\alpha {T^2}{\beta ^2}(M - 3\alpha {c_0})}}{{3{{[\lambda (8\alpha - 5T{\beta ^2})\lambda + 4\alpha - 3T{\beta ^2}]}^2}}} {\text{<}} 0; \end{split} \qquad \dfrac{{\partial e_{\rm s}^{\rm f * }}}{{\partial \lambda }} = - \dfrac{{2T\beta (M - 3\alpha {c_0})(2\alpha - T{\beta ^2})}}{{3{{[\lambda (8\alpha - 5T{\beta ^2}) + 4\alpha - 3T{\beta ^2}]}^2}}} {\text{<}} 0; \qquad \dfrac{{\partial e_{\rm r}^{\rm f * }}}{{\partial \lambda }} = - \dfrac{{{T^2}{\beta ^3}(M - 3\alpha {c_0})}}{{3{{[\lambda (8\alpha - 5T{\beta ^2}) + 4\alpha - 3T{\beta ^2}]}^2}}} {\text{<}} 0; \begin{split} &\qquad \dfrac{{\partial u_{\rm r}^{\rm f * }}}{{\partial \lambda }} =\\ & \dfrac{ T{\left(M - 3\alpha {c_0}\right)^2}\left[\left(5T{\beta ^2} - 8\alpha \right)\left(T{\beta ^2} - \dfrac{{\rm{8}}}{{\rm{3}}}\alpha \right){\lambda ^3} \right. + 9\left(T{\beta ^2} - \dfrac{{\rm{4}}}{{\rm{3}}}\alpha \right)\left(T{\beta ^2} - \dfrac{{\rm{8}}}{{\rm{3}}}\alpha \right){\lambda ^2} + \left(\dfrac{{{\rm{16}}}}{{\rm{3}}}{T^2}{\beta ^4} - \dfrac{{{\rm{62}}}}{{\rm{3}}}T{\beta ^2}\alpha + \dfrac{{{\rm{16}}}}{{\rm{3}}}{\alpha ^2}\right)\lambda + \left. \dfrac{{\rm{2}}}{{\rm{3}}}\left(T{\beta ^2} - \alpha \right)\left(T{\beta ^2} - {\rm{4}}\alpha \right)\right] }{{6{{\left[\lambda \left(8\alpha - 5T{\beta ^2}\right) + 4\alpha - 3T{\beta ^2}\right]}^3}}}{\text{。}} \end{split} 其中,
\left[\left(5T{\beta ^2} \;-\; 8\alpha \right)\left(T{\beta ^2} \;-\; \dfrac{{\rm{8}}}{{\rm{3}}}\alpha \right){\lambda ^3} + 9\left(T{\beta ^2} \;-\; \dfrac{{\rm{4}}}{{\rm{3}}}\alpha \right)\right. \times \left(T{\beta ^2} - \dfrac{{\rm{8}}}{{\rm{3}}}\alpha \right){\lambda ^2} \;+\; \left(\dfrac{{{\rm{16}}}}{{\rm{3}}}{T^2}{\beta ^4} - \dfrac{{{\rm{62}}}}{{\rm{3}}}T{\beta ^2}\alpha \;+\; \dfrac{{{\rm{16}}}}{{\rm{3}}}{\alpha ^2}\right)\lambda \;+\; \dfrac{{\rm{2}}}{{\rm{3}}}\left(T{\beta ^2} \right. −\Bigg. \left. \alpha \right) (T{\beta ^2} - 4\alpha ) \Bigg] {\text{>}} \dfrac{{\rm{1}}}{{\rm{2}}}T{\beta ^2}\alpha \left(5{\lambda ^3} + 9{\lambda ^2} + \dfrac{{{\rm{16}}}}{{\rm{3}}}\lambda + \dfrac{{\rm{2}}}{{\rm{3}}}\right) - T{\beta ^2}\alpha \left(\dfrac{{{\rm{104}}}}{{\rm{3}}}{\lambda ^3} \right. +\left. 60{\lambda ^2} + \dfrac{{{\rm{62}}}}{{\rm{3}}}\lambda + \dfrac{{{\rm{10}}}}{{\rm{3}}}\right)\;+\; {\alpha ^2}\left(\dfrac{{{\rm{64}}}}{{\rm{3}}}{\lambda ^3} \;+\; 32{\lambda ^2} + \dfrac{{{\rm{16}}}}{{\rm{3}}}\lambda \;+\; \dfrac{{\rm{8}}}{{\rm{3}}}\right) {\text{>}} \dfrac{{\rm{1}}}{{\rm{2}}}{\alpha ^2} ×\left( - \dfrac{{{\rm{193}}}}{{\rm{6}}}{\lambda ^3} - \dfrac{{{\rm{111}}}}{{\rm{2}}}{\lambda ^2} - 18\lambda - 3\right) + {\alpha ^2}\left(\dfrac{{{\rm{64}}}}{{\rm{3}}}{\lambda ^3} + 32{\lambda ^2} + \dfrac{{{\rm{16}}}}{{\rm{3}}}\lambda + \dfrac{{\rm{8}}}{{\rm{3}}}\right) ={\alpha ^2}\left(\dfrac{{{\rm{21}}}}{{\rm{4}}}{\lambda ^3} + \dfrac{{{\rm{17}}}}{{\rm{4}}}{\lambda ^2} - \dfrac{{{\rm{11}}}}{{\rm{3}}}\lambda + \dfrac{{\rm{7}}}{{\rm{6}}}\right) {\text{>}} 0 ,即\dfrac{{\partial u_{\rm r}^{\rm f * }}}{{\partial \lambda }} {\text{>}} 0 。\qquad \dfrac{{\partial \pi \,_{\rm s}^{\rm f * }}}{{\partial \lambda }} = - \dfrac{{T{{(M - 3\alpha {c_0})}^2}(2\alpha - T{\beta ^2})}}{{9{{[\lambda (8\alpha - 5T{\beta ^2}) + 4\alpha - 3T{\beta ^2}]}^2}}} {\text{<}} 0; \qquad \dfrac{{\partial \pi \,_{\rm sc}^{\rm f * }}}{{\partial \lambda }} = - \dfrac{{4{T^2}{\beta ^2}\left(\lambda + \dfrac{{\rm{1}}}{{\rm{4}}}\right){{(M - 3\alpha {c_0})}^2}(2\alpha - T{\beta ^2})}}{{9{{[\lambda (8\alpha - 5T{\beta ^2}) + 4\alpha - 3T{\beta ^2}]}^3}}} {\text{<}} 0; \qquad \dfrac{{\partial \pi \,_{\rm r}^{\rm f * }}}{{\partial \lambda }} = - \dfrac{{T{{(M - 3\alpha {c_0})}^2}(2\alpha - T{\beta ^2})\left[T{\beta ^2}\left(\lambda {\rm{ + }}\dfrac{{\rm{4}}}{{\rm{9}}}\right) - \left(\dfrac{{\rm{8}}}{{\rm{9}}}\lambda + \dfrac{{\rm{4}}}{{\rm{9}}}\right)\alpha \right]}}{{{{[\lambda (8\alpha - 5T{\beta ^2}) + 3T{\beta ^2} - 4\alpha ]}^3}}}{\text{。}} 当
T{\beta ^{\rm{2}}} {\text{<}} \alpha {\text{<}} \overline \lambda T{\beta ^{\rm{2}}} 时,\dfrac{{\partial \pi \,_{\rm r}^{\rm f * }}}{{\partial \lambda }} {\text{<}} 0 ;当\overline \lambda T{\beta ^{\rm{2}}} {\text{<}} \alpha {\text{<}} {\rm{2}}T{\beta ^{\rm{2}}} 时,\dfrac{{\partial \pi \,_{\rm r}^{\rm f * }}}{{\partial \lambda }} {\text{>}} 0 。其中,\overline \lambda = \dfrac{{9\lambda + 4}}{{8\lambda + 4}} 。由性质1①可知,最优批发价格、订购量和双边保鲜努力水平都与零售商公平偏好系数负相关。由性质1②可知,供应商利润、供应链利润与零售商公平偏好系数负相关,但零售商效用与其正相关。零售商利润随自身公平偏好系数的变化趋势依赖于市场需求对价格(
\alpha )和生鲜度(\beta )敏感系数的关系:当市场需求更容易受新鲜度影响时,零售商利润与公平偏好系数正相关;当市场需求更容易受到价格影响时,零售商利润与公平偏好系数负相关。4. 基于“批发价格契约+转移支付”的协调机制
通过对批发价格契约下的生鲜农产品供应链分析可知,分散决策的“双重边际效应”使得双边保鲜努力水平决策和零售商订购量都不能达到集中决策下的最优状态,而零售商公平偏好行为又进一步使双边保鲜努力水平、供应链订购量降低进而供应链利润偏离最优。为了克服双重边际效应、缓减零售商公平偏好行为对双边保鲜努力水平和供应链的不利影响,本文在批发价格基础上引入“转移支付”来协调零售商公平偏好下的生鲜农产品供应链,即供应商以较低的批发价格提供生鲜农产品给零售商从而刺激零售商提高订购量,但前提是零售商提前支付给供应商转移支付费。转移支付一方面起到供应、保鲜补助金的作用激励供应商提高保鲜努力水平、降低批发价格;另一方面转移支付起到风险分担的作用,即零售商通过提前支付转移支付给供应商能够获得尽可能低的批发价格和更新鲜的产品,零售商加大订购量,缓减零售商的销售收益风险。如永辉超市总是提前支付一定费用给生鲜农产品供应商用于农业设施投资、生鲜农产品培育改进、生鲜农产品保鲜技术设备引进和提高等,而其生鲜农产品供应商总是以非常低的批发价格提供优质生鲜农产品给永辉超市,使得永辉超市总能通过供应“优质低价”生鲜农产品稳定市场地位、增加竞争力[24]。
引入转移支付后,供应商利润和零售商利润为
\qquad \pi \,_{\rm s}^{\rm nz} = (w - {c_0})q - \dfrac{1}{2}e_{\rm s}^2 + F; (30) \qquad \pi \,_{\rm r}^{\rm nz} = \left[\dfrac{M}{{3\alpha }} + \dfrac{{\beta ({e_{\rm s}} + {e_{\rm r}})}}{\alpha } - \dfrac{q}{{\alpha T}} - w \right]q - \dfrac{1}{2}e_{\rm r}^2 - F{\text{。}} (31) 4.1 零售商公平中性情形
供应商希望零售商提供的转移支付
F 越大越好,但是零售商提供转移支付的前提是提供转移支付后的利润不低于提供之前,同时提供的转移支付能够激励供应商提供最优保鲜努力和最低批发价格。于是,引入转移支付后供应商和零售商的决策问题变为委托代理问题。\qquad \mathop {{\rm{max}}}\limits_{F,w,{e_{\rm s}}} \pi \,_{\rm s}^{\rm nz} = (w - {c_0})q - \dfrac{1}{2}e_{\rm s}^2 + F{\text{。}} (32) \begin{split} & \qquad {\rm{ s.t.}}\\ & \qquad ({\rm{IR}})\pi \,_{\rm r}^{\rm nz} \geqslant \pi \,_{\rm r}^{\rm n * }; \\ & \qquad ({\rm{IC}})\mathop {{\rm{max}}}\limits_{q,{e_{\rm r}}} \pi \,_{\rm r}^{\rm nz} {\text{。}} \end{split} (33) 上述模型中,式(32)表示供应商处于主导地位通过决策零售商提供的转移支付、批发价格和保鲜努力实现利润最大;式(33)表示零售商接受转移支付的参与约束(IR)和激励相容约束(IC),参与约束保证了零售商在支付转移支付后的利润不低于转移之前从而零售商接受转移支付;激励相容约束确保了零售商选择最优的订购量和保鲜努力实现自身总利润最大化。
由式(31)可得转移支付
F 不影响\pi \,_{\rm r}^{\rm nz} 函数的凹凸性,于是存在唯一最优的零售商保鲜努力水平和订购量实现\pi \,_{\rm r}^{\rm nz} 的最大化。令\dfrac{{\partial \pi \,_{\rm r}^{\rm nz}}}{{\partial q}} = 0 和\dfrac{{\partial \pi \,_{\rm r}^{\rm nz}}}{{\partial {e_{\rm r}}}} = 0 可以得到零售商最优订购量{q^{\rm nz * }}(w,{e_{\rm s}}) 和保鲜努力水平e_{\rm r}^{\rm nz * }(w,{e_{\rm s}}) 分别为\qquad {q^{\rm nz * }}(w,{e_{\rm s}}) = \dfrac{{\alpha T(M - 3\alpha w + 3\beta {e_{\rm s}})}}{{3(2\alpha - T{\beta ^2})}}; \qquad e_{\rm r}^{\rm nz * }(w,{e_{\rm s}}) = \dfrac{{\beta T(M - 3\alpha w + 3\beta {e_{\rm s}})}}{{3(2\alpha - T{\beta ^2})}}{\text{。}} 由式(31)和(32)可知,零售商利润关于转移支付
F 严格线性递减,供应商要求的最大转移支付满足\pi \,_{\rm r}^{\rm nz} = \pi \,_{\rm r}^{\rm n * } ,即供应商要求的转移支付刚好满足零售商利润等于不提供的情形,转移支付继续增加就会迫使零售商退出博弈、终止合作。通过\pi \,_{\rm r}^{\rm nz} = \pi \,_{\rm r}^{\rm n * } 可得{F^{\rm nz}}(q,w,{e_{\rm s}},{e_{\rm r}}) ,将{q^{\rm nz * }}(w,{e_{\rm s}}) 、e_{\rm r}^{\rm nz * }(w,{e_{\rm s}}) 和{F^{\rm nz}}(q,w,{e_{\rm s}},{e_{\rm r}}) 代入式(33),同时令\dfrac{{\partial \pi \,_{\rm s}^{\rm nz}}}{{\partial w}} = 0 ,\dfrac{{\partial \pi \,_{\rm s}^{\rm nz}}}{{\partial {e_{\rm s}}}} = 0 得供应商最优保鲜努力水平e_{\rm s}^{\rm nz * } 和批发价格{w^{\rm nz * }} 分别为\qquad e_{\rm s}^{\rm nz * } = \dfrac{{\beta T(M - 3\alpha {c_0})}}{{6(\alpha - T{\beta ^2})}}; (34) \qquad {w^{\rm nz * }} = {c_0}{\text{。}} (35) 将式(34)、(35)代入
{q^{\rm nz * }}(w,{e_{\rm s}}) 、e_{\rm r}^{\rm nz * }(w,{e_{\rm s}}) 和{F^{\rm nz}}(q, w,{e_{\rm s}},{e_{\rm r}}) 中,可得零售商最优订购量{q^{\rm nz * }} 和保鲜努力水平e_{\rm r}^{\rm nz * } 分别为\qquad {q^{\rm nz * }} = \dfrac{{\alpha T(M - 3\alpha {c_0})}}{{6(\alpha - T{\beta ^2})}}; (36) \qquad e_{\rm r}^{\rm nz * } = \dfrac{{\beta T(M - 3\alpha {c_0})}}{{6(\alpha - T{\beta ^2})}}{\text{。}} (37) 于是,可以计算转移支付、零供双方和供应链系统利润分别为
\qquad {F^{\rm nz * }} = \dfrac{{5T{{(2\alpha - T{\beta ^2})}^2}{{(M - 3\alpha {c_0})}^2}\left(\dfrac{{\rm{6}}}{{\rm{5}}}\alpha - T{\beta ^2}\right)}}{{648{{(\alpha - T{\beta ^2})}^2}{{\left(\dfrac{{\rm{4}}}{{\rm{3}}}\alpha - T{\beta ^2}\right)}^2}}}; (38) \qquad \pi \,_{\rm s}^{\rm nz * } = \dfrac{{T{{(M - 3\alpha {c_0})}^2}(7{T^2}{\beta ^4} - 18T{\beta ^2}\alpha + 12{\alpha ^2})}}{{324{{\left(\dfrac{{\rm{4}}}{{\rm{3}}}\alpha - T{\beta ^2}\right)}^2}(\alpha - T{\beta ^2})}}; (39) \qquad \pi \,_{\rm r}^{\rm nz * } = \dfrac{{T{{(M - 3\alpha {c_0})}^2}(2\alpha - T{\beta ^2})}}{{18{{(4\alpha - 3T{\beta ^2})}^2}}}; (40) \qquad \pi \,_{\rm sc}^{\rm nz * } = \dfrac{{T{{(M - 3\alpha {c_0})}^2}}}{{36(\alpha - T{\beta ^2})}}{\text{。}} (41) 命题2 ①
{w^{\rm nz * }} = {c_0} ,e_{\rm s}^{\rm nz * } = e_{\rm r}^{\rm nz * } = e_{\rm r}^{\rm c * } = e_{\rm s}^{\rm c * } ,{q^{\rm nz * }} = {q^{\rm c * }} ;②\pi \,_{\rm sc}^{\rm nz * } = \pi \,_{\rm sc}^{\rm c * } ,\pi \,_{\rm r}^{\rm nz * } = \pi \,_{\rm r}^{\rm n * } ,\pi \,_{\rm s}^{\rm nz * } {\text{>}} \pi \,_{\rm s}^{\rm n * } 。由命题2可知,引入转移支付后,零、供双边保鲜努力水平相等且实现了集中决策下要求的最优双边保鲜努力水平,零售商订购量和供应链利润都与集中决策情形相同,表明引入转移支付能够使供应链实现协调。引入转移支付后,零售商利润不变但供应商利润增加,说明供应商通过引入转移支付获得了供应链中所有增加的利润。
结合命题1①和命题2①可得到
e_{\rm s}^{\rm nz * } {\text{>}} e_{\rm s}^{\rm n * } 和e_{\rm r}^{\rm nz * } {\text{>}} e_{\rm r}^{\rm n * } ,即零售商通过对供应商支付转移支付费用,激励供应商提高保鲜努力(e_{\rm s}^{\rm nz * } {\text{>}} e_{\rm s}^{\rm n * } ),获得较低批发价格({w^{\rm nz * }} = {c_0} ),增加订购量({q^{\rm nz * }} = {q^{\rm c * }} {\text{>}} {q^{\rm n * }} ),为降低损耗而提高自身保鲜努力水平,并使供应链在此水平上实现协调(\pi \,_{\rm sc}^{\rm nz * } = \pi \,_{\rm sc}^{\rm c * } )。4.2 零售商公平偏好情形
由于批发价格契约不能协调供应链,而零售商公平偏好行为会进一步降低双边保鲜努力水平和供应链利润,使供应链进一步偏离最优。4.1节在批发价格契约基础上引入转移支付能够保证双边保鲜努力水平、订购量和供应链利润实现最优,即“批发价格 + 转移支付”的组合契约能够协调零售商公平中性情形下的生鲜农产品供应链。该部分拟检验“批发价格 + 转移支付”的组合契约能否协调零售商公平偏好下的生鲜农产品供应链。
引入转移支付后,由式(30)和(31),公平偏好的零售商效用为
\begin{split} & \qquad u_{\rm r}^{\rm fz } = \pi \,_{\rm r}^{\rm fz } - \lambda (\pi \,_{\rm s}^{\rm fz } - \pi \,_{\rm r}^{\rm fz }) = (1 + \lambda )\left[\left(\dfrac{M}{{3\alpha }} + \dfrac{{\beta ({e_{\rm s}} + {e_{\rm r}})}}{\alpha } -\right.\right. \\ & \left. \left.\dfrac{q}{{\alpha T}} - w \right) - \dfrac{1}{2}e_{\rm r}^2 \right] - \lambda \left[(w - {c_0})q - \dfrac{1}{2}e_{\rm s}^2\right] - (2\lambda + 1)F {\text{。}} \end{split} (42) 同零售商公平中性情形,供应商和零售商之间的委托代理问题表示为
\qquad \mathop {{\rm{max}}}\limits_{F,w,{e_{\rm s}}} \pi \,_{\rm s}^{\rm fz } = (w - {c_0})q - \dfrac{1}{2}e_{\rm s}^2 + F{\text{。}} (43) \begin{split} & \qquad {\rm{ s.t.}}\\ & \qquad ({\rm{IR}})u_{\rm r}^{\rm fz } \geqslant u_{\rm r}^{\rm f * } ;\\ & \qquad ({\rm{IC}})\mathop {{\rm{max}}}\limits_{q,{e_{\rm r}}} u_{\rm r}^{\rm fz }{\text{。}} \end{split} (44) 上述模型中,式(43)表示供应商处于主导地位通过决策零售商提供的转移支付、批发价格和保鲜努力实现利润最大;式(44)表示零售商接受转移支付的参与约束(IR)和激励相容约束(IC),参与约束保证了零售商在支付转移支付后的效用不低于转移之前从而零售商接受转移支付;激励相容约束确保零售商选择最优的订购量和保鲜努力实现自身总效用最大化。同公平中性条件下的计算和分析过程,可得引入转移支付后各方最优决策和利润
\qquad e_{\rm s}^{\rm fz * } = \dfrac{{\beta T(M - 3\alpha {c_0})}}{{6(\alpha - T{\beta ^2})}}; (45) \qquad {w^{\rm fz * }} = {c_0}; (46) \qquad {q^{\rm fz * }} = \dfrac{{\alpha T(M - 3\alpha {c_0})}}{{6(\alpha - T{\beta ^2})}}; (47) \qquad e_{\rm r}^{\rm fz * } = \dfrac{{\beta T(M - 3\alpha {c_0})}}{{6(\alpha - T{\beta ^2})}}; (48) \begin{split} \qquad {F^{\rm fz * }} = \dfrac{ T(T{\beta ^2} - 2\alpha ){(M - 3\alpha {c_0})^2}\Big[( - 4{\lambda ^3} - 8{\lambda ^2} - 5\lambda - 1)\alpha \Big.+\left. T{\beta ^2}\alpha \left(\dfrac{3}{2}{\lambda ^3} + \dfrac{{19}}{3}{\lambda ^2} + \dfrac{{11}}{2}\lambda + \dfrac{4}{3}\right) + {T^2}{\beta ^4}\left({\lambda ^3} - \dfrac{1}{{12}}{\lambda ^2} - \dfrac{7}{6}\lambda - \dfrac{5}{{12}}\right)\right] }{{6(1 + 2\lambda ){{(\alpha - T{\beta ^2})}^2}{{[\lambda (8\alpha - 5T{\beta ^2}) + 4\alpha - 3T{\beta ^2}]}^2}}}; \end{split} (49) \qquad \pi \,_{\rm s}^{\rm fz * } = \dfrac{ T(1 + \lambda ){(M - 3\alpha {c_0})^2}[(48{\lambda ^2} + 48\lambda + 12){\alpha ^2} - (58{\lambda ^2} \\ + 66\lambda + 18)T{\beta ^2}\alpha + (19{\lambda ^2} + 24\lambda + 7){T^2}{\beta ^4}] }{{36(1 + 2\lambda )(\alpha - T{\beta ^2}){{[\lambda (8\alpha - 5T{\beta ^2}) + {\rm{4}}\alpha - 3T{\beta ^2}]}^{\rm{2}}}}}; (50) \qquad \pi \,_{\rm r}^{\rm fz * } = \dfrac{ T{(M - 3\alpha {c_0})^2}(T{\beta ^2} - 2\alpha )[( - 40{\lambda ^3} - 48{\lambda ^2} - 18\lambda - 2)\alpha + (31{\lambda ^3} + 42{\lambda ^2} + 17\lambda + 2)T{\beta ^2}] }{{36(1 + 2\lambda )(\alpha - T{\beta ^2}){{[\lambda (8\alpha - 5T{\beta ^2}) + 4\alpha - 3T{\beta ^2}]}^2}}}; (51) \qquad \pi \,_{\rm sc}^{\rm fz * } = \dfrac{{T{{(M - 3\alpha {c_0})}^2}}}{{36(\alpha - T{\beta ^2})}}{\text{。}} (52) 引入转移支付后,通过计算和比较可以得到命题3和性质2。
命题3 ①
{w^{\rm fz * }} = {c_0} ,e_{\rm r}^{\rm fz * } = e_{\rm r}^{\rm c * } = e_{\rm s}^{\rm fz * } = e_{\rm s}^{\rm c * } ,{q^{\rm fz * }} = {q^{\rm c * }} ;②
\pi \,_{\rm s}^{\rm fz * } {\text{>}} \pi \,_{\rm s}^{\rm f * } ,\pi \,_{\rm r}^{\rm fz * } {\text{>}} \pi \,_{\rm r}^{\rm f * } ,\pi \,_{\rm sc}^{\rm fz * } = \pi \,_{\rm sc}^{\rm c * } ,\left| {\pi \,_{\rm s}^{\rm fz * } - \pi \,_{\rm s}^{\rm f * }} \right| {\text{>}} \left| {\pi \,_{\rm r}^{\rm fz * } - }\right. \left. {\pi \,_{\rm r}^{\rm f * }} \right| 。证明同命题1,故此处证明略。
由命题3①可知,零售商公平偏好下引入转移支付后的批发价格刚好等于供应商成本,零供双边保鲜努力水平相等且都实现集中决策下的最优,零售商订购量等于集中决策下供应链所要求的最优订购量。由命题3②可知,引入转移支付后即使零售商具有公平偏好行为,供应商、零售商利润都得到改进且供应商利润增加幅度大于零售商,供应链利润实现最优。
结合命题1①和命题3①可得到
e_{\rm s}^{\rm fz * } {\text{>}} e_{\rm s}^{\rm f * } 和e_{\rm r}^{\rm fz * } {\text{>}} e_{\rm r}^{\rm f * } ,即零售商通过对供应商支付转移支付费用,激励供应商提高保鲜努力(e_{\rm s}^{\rm fz * } {\text{>}} e_{\rm s}^{\rm f * } ),获得较低批发价格({w^{\rm fz * }} = {c_0} ),增加订购量({q^{\rm fz * }} = {q^{\rm c * }} {\text{>}} {q^{\rm f * }} ),为降低损耗而提高自身保鲜努力水平,并使供应链在此水平上实现协调(\pi \,_{\rm sc}^{\rm fz * } = \pi \,_{\rm sc}^{\rm c * } )。性质2 ①
\dfrac{{\partial e_{\rm r}^{\rm fz * }}}{{\partial \lambda }} \;= \; \dfrac{{\partial e_{\rm s}^{\rm fz * }}}{{\partial \lambda }} \;= \; \dfrac{{\partial {q^{\rm fz * }}}}{{\partial \lambda }} \;= \; \dfrac{{\partial {w^{\rm fz * }}}}{{\partial \lambda }} \;= \; 0 ,\dfrac{{\partial {F^{\rm fz * }}}}{{\partial \lambda }} \;{\text{<}} \; 0 ;②\dfrac{{\partial \pi \,_{\rm r}^{\rm fz * }}}{{\partial \lambda }} \;{\text{>}}\; 0 ,\dfrac{{\partial \pi \,_{\rm s}^{\rm fz * }}}{{\partial \lambda }} \;{\text{<}}\; 0 ,\dfrac{{\partial \pi \,_{\rm s}^{\rm fz * }}}{{\partial \lambda }} = - \dfrac{{\partial \pi \,_{\rm r}^{\rm fz * }}}{{\partial \lambda }} ,\dfrac{{\partial \pi \,_{\rm sc}^{\rm fz * }}}{{\partial \lambda }} = 0 。证明同性质1,故此处证明略。
由性质2①可知,引入转移支付后零售商公平偏好行为不影响双边最优保鲜努力水平决策、订购量和批发价格决策,转移支付随零售商公平偏好严格递减;由性质2②可知,虽然供应商利润随零售商公平偏好递减、零售商利润随公平偏好递增,但是双方利润受公平偏好影响的幅度相同,因此供应链利润不仅能实现协调且不受零售商公平偏好影响。
结合命题2和命题3可知,无论零售商是否关注公平,基于“批发价格 + 转移支付”的组合契约都能协调生鲜农产品供应链、激励供应商和零售商自发投入供应链系统所要求的最优保鲜努力水平、帕累托改进供应商和零售商利润。
根据式(38)和(49),可得命题4。
命题4
\dfrac{{\partial {F^{\rm fz * }}}}{{\partial \lambda }} {\text{<}} 0 ,{\left. {{F^{\rm fz }}} \right|_{\lambda = 0}} = {F^{\rm nz}} 。命题4说明供应商所要求的转移支付费用与零售商公平偏好负相关,且当零售商公平偏好系数为零时,公平中性下转移支付与公平偏好下转移支付相等,说明基于“批发价格契约 + 转移支付”的组合契约能自动协调零售商公平中性和公平偏好的生鲜农产品供应链。
结合命题1~3可得结论1。
结论1 无论零售商是否关注公平,批发价格契约都不能协调生鲜农产品供应链,且零售商的公平偏好行为会进一步降低零供双边保鲜努力水平和供应链利润;而“批发价格 + 转移支付”的组合契约总能协调生鲜农产品供应链,激励供应商和零售商自发实现最优保鲜努力水平和供应链协调、帕累托改进供应链成员利润。
5. 数值分析
为验证“批发价格契约 + 转移支付”组合契约协调双边保鲜努力下生鲜农产品供应链的有效性及零售商公平偏好对双边保鲜努力水平、最优订购量和供应链利润的影响,这里借鉴张旭[22]数值分析所用参数:
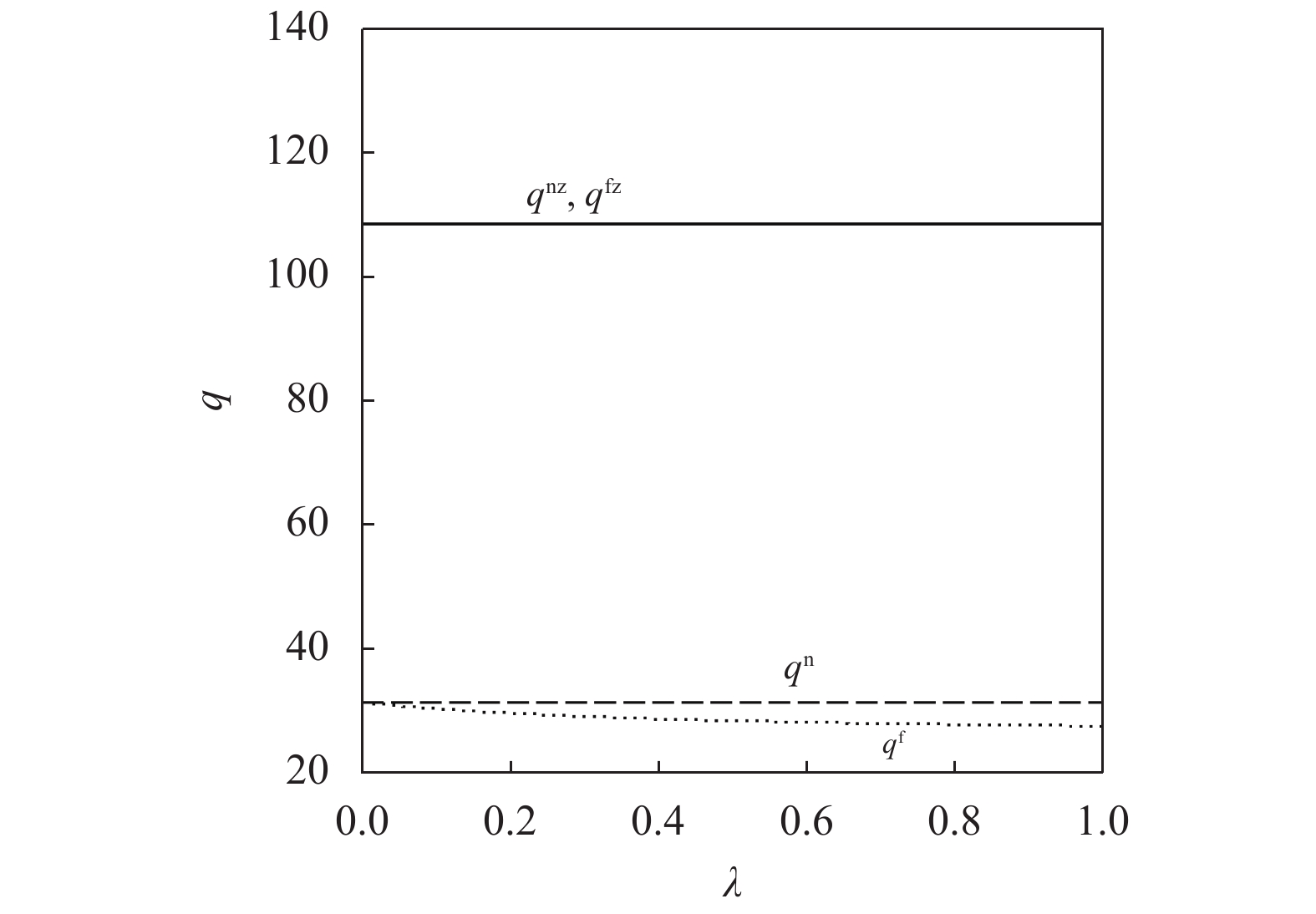
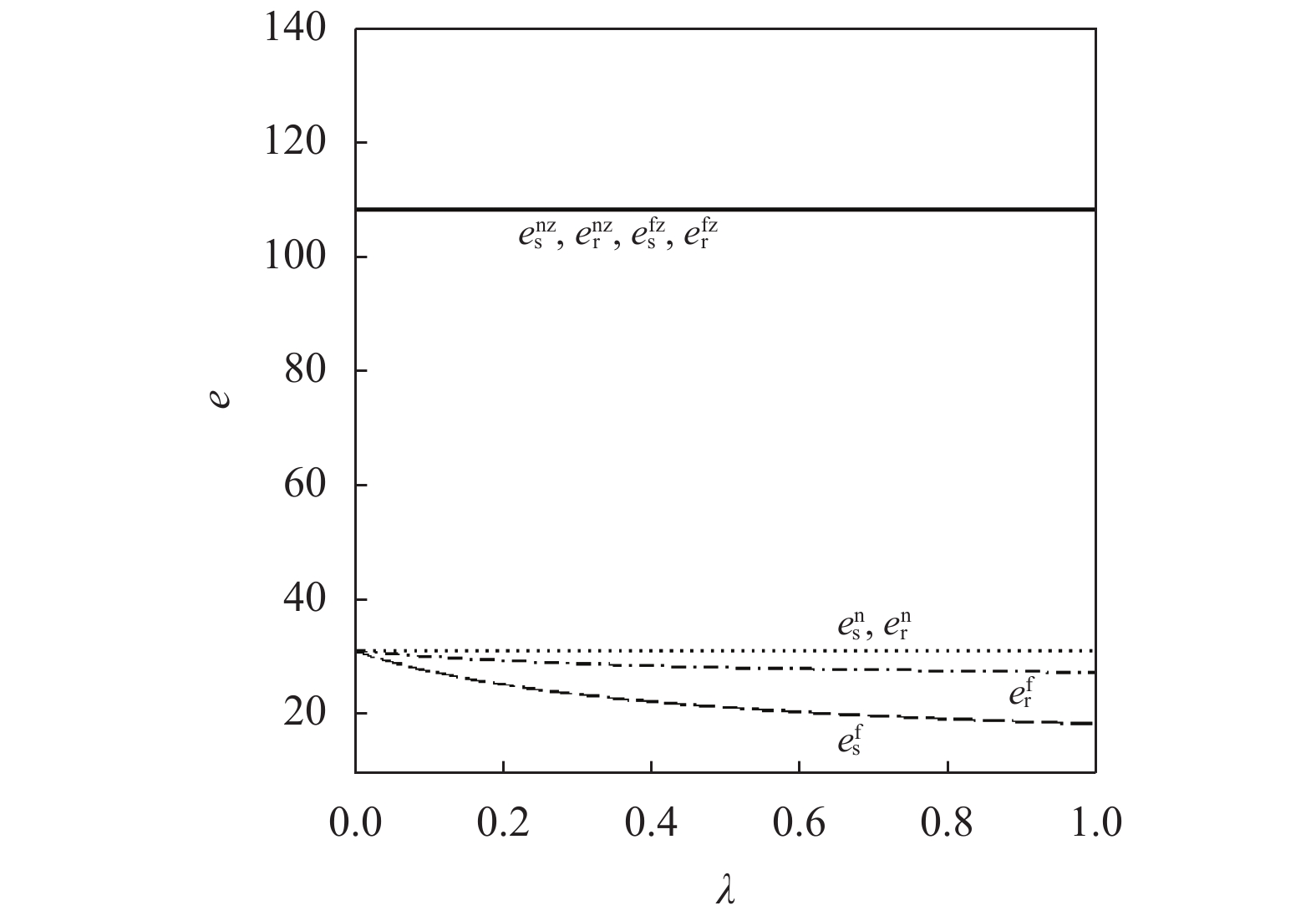
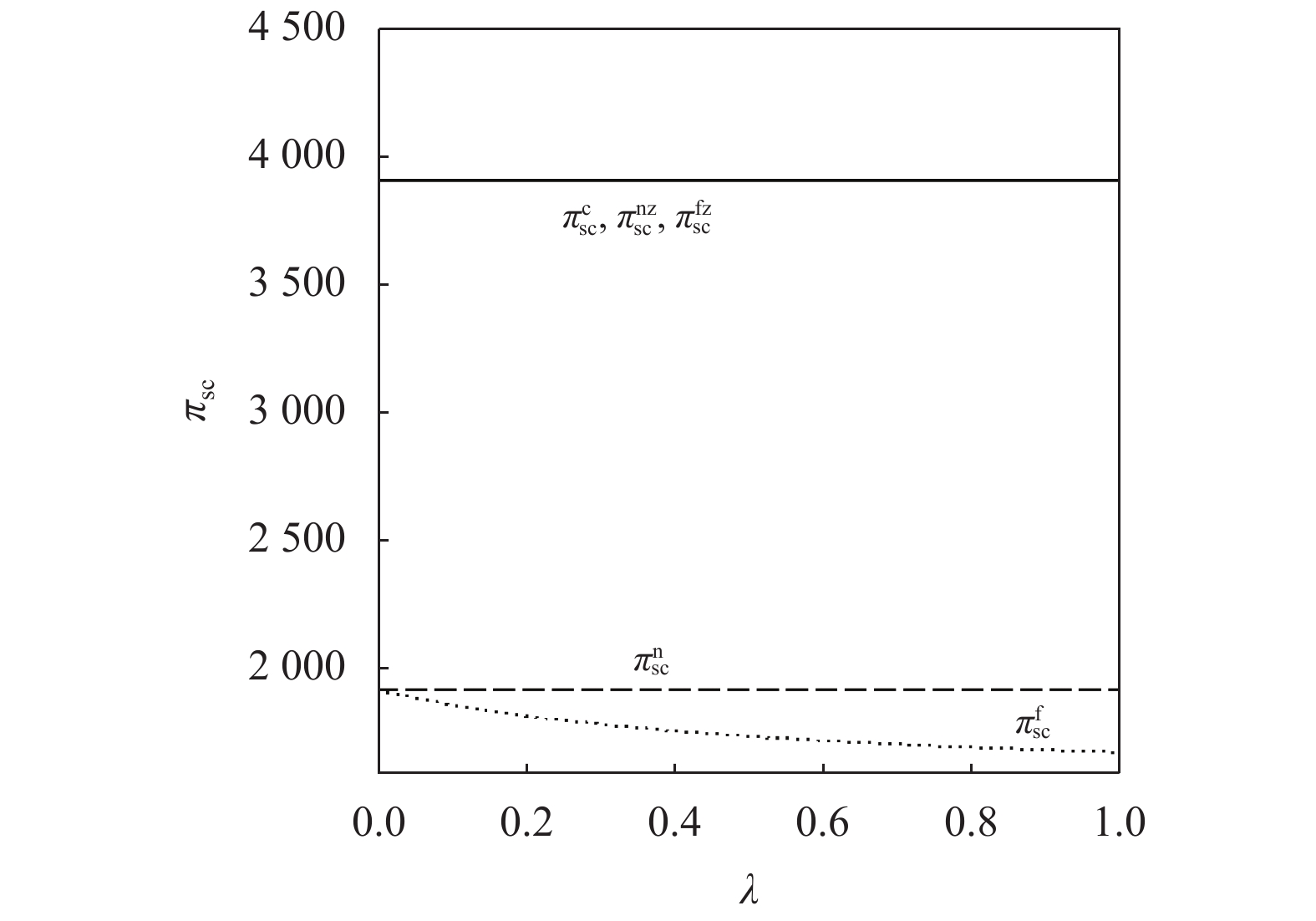
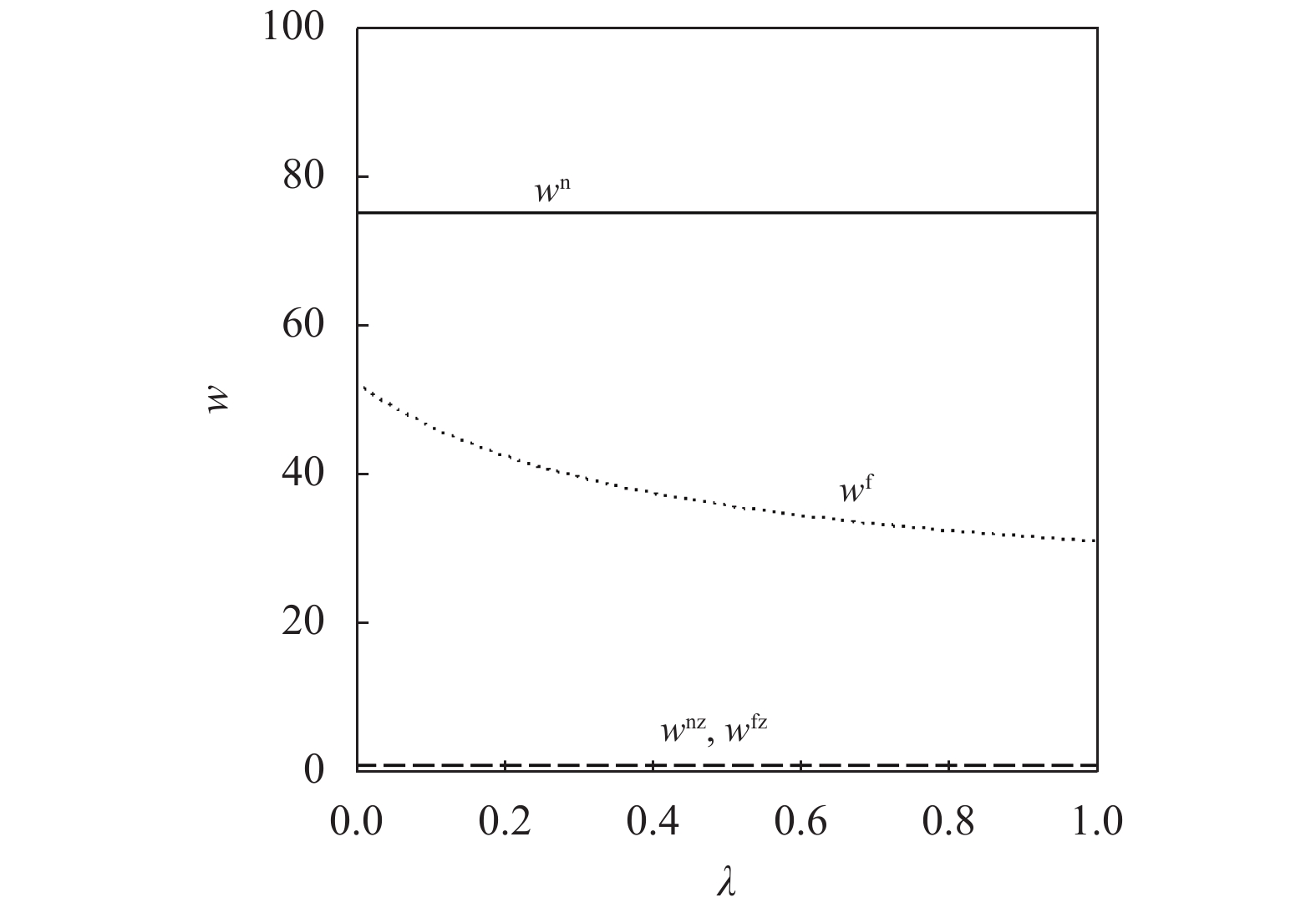
{c_0} = 1 、{\eta _{\rm{0}}}{\rm{ = 0}}{\rm{.5}} 、a = 110 ,\lambda \in [0,1] 。为满足T{\beta ^{\rm{2}}} {\text{<}} \alpha {\text{<}} 2T{\beta ^{\rm{2}}} ,设\alpha = \beta = 1.5 ,T = 0.5 。经计算易得集中决策下的最优值分别为{q^{\rm c * }} = 108.25 、e_{\rm s}^{\rm c * } = 108.25 、e_{\rm r}^{\rm c * } = 108.25 、\pi \,_{\rm sc}^{\rm c * } = 3\;906.02 。依据参数的取值可得零售商公平偏好下,公平偏好系数对供应链仅采用批发价格契约和批发价格契约 + 转移支付组合策略的最优决策及各方利润的影响并与公平中性情形进行比较分析,利用MAPLE绘制图1~7。由图1 ~ 3可以看出,基于批发价格契约的零售商公平偏好下,供应链批发价格、订购量、双边保鲜努力水平随零售商公平偏好增强而降低,与性质1①一致,进一步说明零售商公平偏好对供应链不利,并使供应链偏离集中决策最优情形。结合图2、3和7,发现引入转移支付两种情形下,供应链双边保鲜努力水平、订购量与集中决策情形一致均高于基于批发价格契约的两种情形,供应链利润达到集中决策最优水平,进一步验证命题2和命题3,说明“批发价格 + 转移支付”的组合契约可以协调生鲜农产品供应链,这与结论1一致。
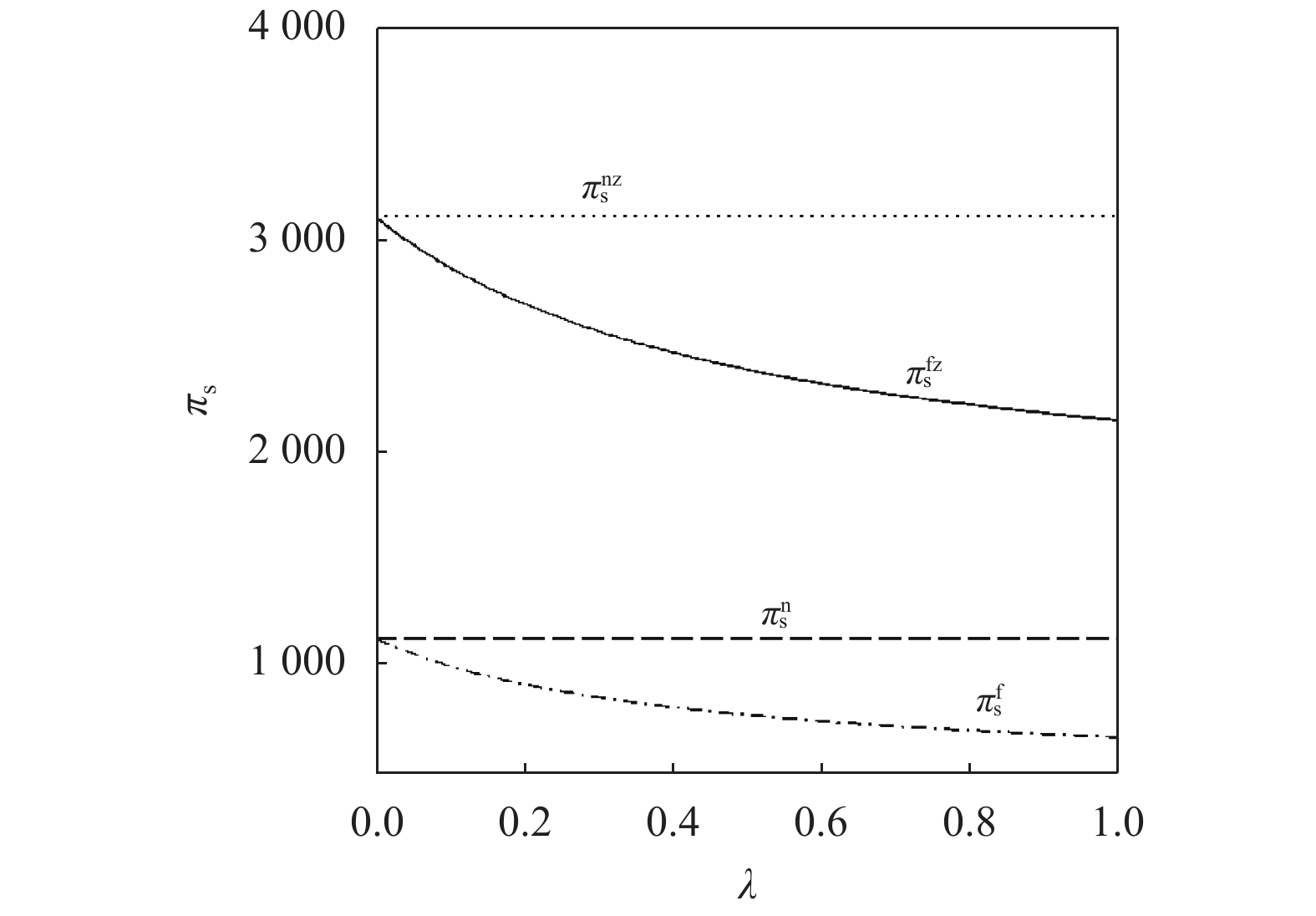
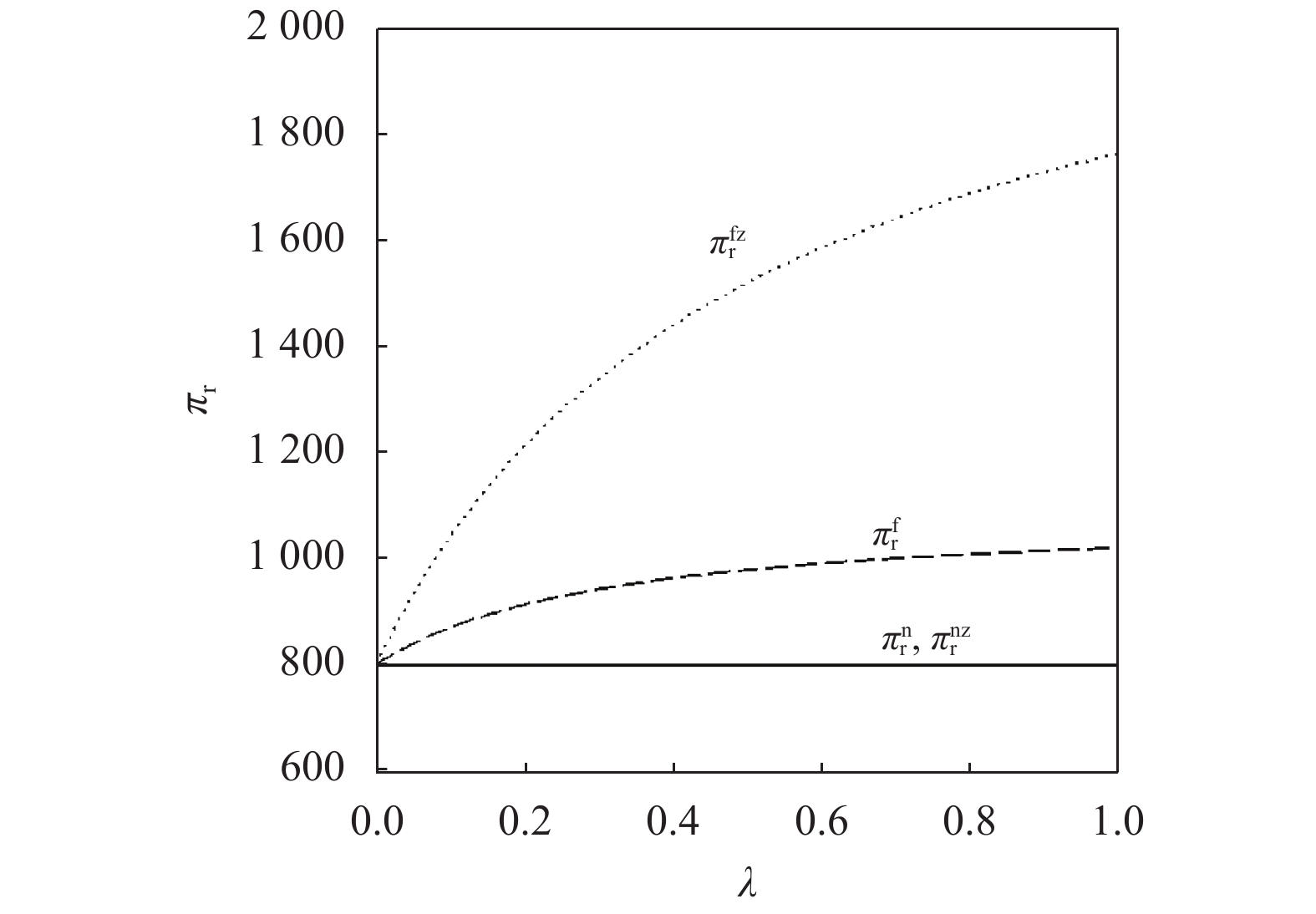
另外,由图4 ~ 6可以看出,零售商公平中性下,“批发价格 + 转移支付”的组合策略不会影响零售商利润,但会使供应商利润、供应链利润明显增加,这说明供应链因引入转移支付而增加的利润全部流向供应商,此时实现了供应商单方利润的帕累托改进。零售商公平偏好时,不管是否引入转移支付,供应商利润随公平偏好增强而降低,而零售商利润、效用均上升,进一步验证性质1②和性质2②。同时,在“批发价格 + 转移支付”组合策略下,零、供双方的利润均高于仅采用批发价格契约情形,说明“批发价格 + 转移支付”实现了供应链成员利润的帕累托改进,这与命题3②的结论一致。
6. 结语
本文考虑生鲜农产品特征和供应链成员公平偏好,分别在批发价格契约和“批发价格 + 转移支付”协调机制下对比分析零供双方决策,研究零售商公平偏好对双边保鲜努力和最优决策的影响,通过数值算例验证“批发价格 + 转移支付”组合协调机制的有效性。研究发现:1) 在批发价格契约下,供应链利润、批发价格、订购量和双边保鲜努力均与零售商公平偏好呈负相关,说明零售商公平偏好不利于生鲜农产品供应链,会使供应链偏离集中决策最优。2) 不论零售商是否具有公平偏好,批发价格契约均不能实现生鲜农产品供应链协调,但“批发价格 + 转移支付”组合契约不仅能实现生鲜农产品供应链协调,还能实现供应链成员利润的帕累托改进。3) 基于“批发价格 + 转移支付”组合契约,引入的转移支付能自动协调零售商公平中性和公平偏好情形下的生鲜农产品供应链。
本文虽然在研究生鲜农产品供应链双边保鲜努力优化下考虑了零售商公平偏好,但还存在以下不足之处。首先,仅考虑零售商公平偏好,但现实中供应商也并非完全理性,供应商也会关注利润分配的公平。未来研究可以考虑供应商公平偏好对生鲜农产品供应链的影响。其次,是在确定性市场需求下对零供决策进行研究,但现实中市场需求大多是随机的,因此未来研究可以在不确定性需求下分析公平偏好对生鲜供应链决策的影响,以便得到更符合实际的结论。
-
[1] 吴瑞雯. 大型综合超市生鲜食品管理问题及对策研究——宁波沃尔玛为例[J]. 商, 2016(34): 51-52. [2] 王道平, 朱梦影, 王婷婷. 生鲜供应链保鲜努力成本分担契约研究[J]. 工业工程与管理, 2020, 25(2): 36-43. WANG Daoping, ZHU Mengying, WANG Tingting. Research on the cost sharing contract of fresh-product supply chain's fresh-keeping efforts[J]. Industrial Engineering and Management, 2020, 25(2): 36-43.
[3] CAI X Q, CHEN J, XIAO Y B, et al. Optimization and coordination of fresh product supply chains with freshness-keeping effort[J]. Production and Operations Management, 2010, 19(3): 261-278.
[4] LEE Y P, DYE C Y. An inventory model for deteriorating items under stock-dependent demand and controllable deterioration rate[J]. Computers & Industrial Engineering, 2012, 63(2): 474-482.
[5] 王磊, 但斌. 考虑消费者效用的生鲜农产品供应链保鲜激励机制研究[J]. 管理工程学报, 2015, 29(1): 200-206. DOI: 10.3969/j.issn.1004-6062.2015.01.026 WANG Lei, DAN Bin. The incentive mechanism for preservation in fresh agricultural supply chain considering consumer utility[J]. Journal of Industrial Engineering and Engineering Management, 2015, 29(1): 200-206. DOI: 10.3969/j.issn.1004-6062.2015.01.026
[6] SEO S, JANG S, MIAO L, et al. The impact of food safety events on the value of food-related firms: an event study approach[J]. International Journal of Hospitality Management, 2017, 33(1): 153-164.
[7] 姚冠新, 戴盼倩, 徐静, 等. 双重信息不对称下生鲜农产品物流外包保鲜激励机制研究[J]. 工业工程与管理, 2018, 23(4): 156-162. YAO Guanxin, DAI Panqian, XU Jing, et al. Research on the fresh incentive mechanism for agricultural products logistics outsourcing under the framework of dual information asymmetry[J]. Industrial Engineering and Management, 2018, 23(4): 156-162.
[8] 曹裕, 吴堪, 熊寿遥. 生鲜供应链中保鲜努力投入及订货定价研究[J]. 运筹与管理, 2019, 28(10): 100-109. CAO Yu, WU Kan, XIONG Shouyao. Research on fresh-keeping effort, ordering and pricing in fresh supply chain[J]. Operations Research and Management Science, 2019, 28(10): 100-109.
[9] 曹武军, 陈志斐. 农业保险对生鲜农产品供应链合作关系的影响研究[J]. 工业工程, 2016, 19(5): 88-98. DOI: 10.3969/j.issn.1007-7375.2016.05.013 CAO Wujun, CHEN Zhifei. A study of the effect of agricultural insurance on the supply chain of fresh agricultural products[J]. Industrial Engineering Journal, 2016, 19(5): 88-98. DOI: 10.3969/j.issn.1007-7375.2016.05.013
[10] CUI T H, RAJU J S, ZHANG Z J. Fairness and channel coordination[J]. Management Science, 2007, 53(8): 1303-1314. DOI: 10.1287/mnsc.1060.0697
[11] CALISKAN-DEMIRAG O, CHEN Y, LI J. Channel coordination under fairness concerns and nonlinear demand[J]. European Journal of Operational Research, 2010, 207(3): 1321-1326. DOI: 10.1016/j.ejor.2010.07.017
[12] DU S F, NIE T F, CHU C B, et al. Newsvendor model for a dyadic supply chain with Nash bargaining fairness concerns[J]. International Journal of Production Research, 2014, 52(17): 5070-5085. DOI: 10.1080/00207543.2014.895446
[13] CHOI S, PAUL R. The role of fairness in competitive supply chain relationships: an experimental study[J]. European Journal of Operational Research, forthcoming, 2016, 251(3): 798-813. DOI: 10.1016/j.ejor.2015.12.001
[14] ZHANG F, MA J H. Research on the complex features about a dual-channel supply chain with a fair caring retailer[J]. Communications in Nonlinear Science and Numerical Simulation, 2016, 30(1): 151-167.
[15] 林强, 覃燕红. 不同公平关切下的供应链定价决策分析[J]. 工业工程, 2016, 19(2): 33-37. DOI: 10.3969/j.issn.1007-7375.2016.02.006 LIN Qiang, QIN Yanhong. Pricing decisions of supply chain under different fairness concern[J]. Industrial Engineering Journal, 2016, 19(2): 33-37. DOI: 10.3969/j.issn.1007-7375.2016.02.006
[16] 浦徐进, 金德龙. 公平偏好、参照点效应和三级供应链的运作[J]. 控制与决策, 2015, 30(5): 859-864. PU Xujin, JIN Delong. Fairness preference, reference point effect and operation research in three layer supply chains[J]. Control and Decision, 2015, 30(5): 859-864.
[17] 覃燕红, 魏光兴. 批发价格契约下基于公平偏好信息结构演进的行为博弈分析[J]. 工业工程与管理, 2015, 20(4): 100-107. DOI: 10.3969/j.issn.1007-5429.2015.04.015 QIN Yanhong, WEI Guangxing. Behavior game analysis about the evolution based on information structure of fairness concern under wholesale price contract[J]. Industrial Engineering and Management, 2015, 20(4): 100-107. DOI: 10.3969/j.issn.1007-5429.2015.04.015
[18] 覃燕红, 古玻, 魏光兴. 公平关切下供应链效率和公平度动态演进分析[J]. 工业工程与管理, 2019, 24(4): 40-46. QIN Yanhong, GU Bo, WEI Guangxing. Dynamic evolution of supply chain efficiency and fairness degree under fairness concern[J]. Industrial Engineering and Management, 2019, 24(4): 40-46.
[19] 曹武军, 李新艳. 供应商公平关切对鲜活农产品双渠道供应链协调研究[J]. 郑州大学学报(理学版), 2014, 46(3): 115-118. CAO Wujun, LI Xinyan. Study on dual-channel supply chain coordination of fresh agricultural product with the fairness concern supplier[J]. Journal of Zhengzhou University (Natural Science Edition), 2014, 46(3): 115-118.
[20] 洪美娜, 孙玉玲, 石岿然. 考虑公平关切的鲜活农产品供应链订货决策[J]. 工业工程, 2014, 17(2): 99-105. DOI: 10.3969/j.issn.1007-7375.2014.02.016 HONG Meina, SUN Yuling, SHI Kuiran. Ordering decision of fresh agricultural product supply chain with fairness concern[J]. Industrial Engineering Journal, 2014, 17(2): 99-105. DOI: 10.3969/j.issn.1007-7375.2014.02.016
[21] 张旭, 张庆. 保鲜控制损耗下考虑公平关切的生鲜品供应链协调[J]. 系统科学学报, 2017, 25(3): 112-116. ZHANG Xu, ZHANG Qing. Coordination of fresh agricultural supply chain considering fairness concerns under controlling the loss by freshness-keeping[J]. Journal of Systems Science, 2017, 25(3): 112-116.
[22] 张旭, 张庆. 零售商公平关切下的生鲜品供应链协调机制[J]. 系统工程学报, 2017, 32(4): 461-473. ZHANG Xu, ZHANG Qing. Coordination mechanism for fresh agricultural supply chain under the retailer's fairness concerns[J]. Journal of Systems Engineering, 2017, 32(4): 461-473.
[23] 熊峰, 袁俊, 王猛, 等. 公平偏好下生鲜农产品质量投入与定价研究[J]. 软科学, 2017, 31(4): 122-127. XIONG Feng, YUAN Jun, WANG Meng, et al. Study on the quality investment and pricing of fresh agricultural products under the fairness preference[J]. Soft Science, 2017, 31(4): 122-127.
[24] 李文婷, 胡北忠. 供应链视角下永辉超市生鲜物流成本管理分析[J]. 企业科技与发展, 2019(9): 252-253. DOI: 10.3969/j.issn.1674-0688.2019.09.113 -
期刊类型引用(11)
1. 曹细玉,覃艳华. 保鲜努力和新鲜度参照效应下生鲜农产品供应链最优决策及协调. 江西师范大学学报(自然科学版). 2024(06): 604-612 .  百度学术
百度学术
2. 杨扬,刘语瑶. 考虑通关水平的跨境物流服务供应链契约协调机制研究. 工业工程. 2023(01): 52-62+90 .  本站查看
本站查看
3. 徐聪. 电商平台补贴下的生鲜农产品供应链决策研究. 中国储运. 2023(04): 118-120 .  百度学术
百度学术
4. 覃燕红,王少杰. 不利天气影响下考虑农户公平关切的农产品供应链协调机制研究. 系统科学与数学. 2023(03): 595-609 .  百度学术
百度学术
5. 罗云伟. 我国生鲜农产品供应链发展策略研究. 物流工程与管理. 2023(04): 76-78 .  百度学术
百度学术
6. 潘晓飞,张涛. 考虑损失规避的生鲜品供应链保鲜努力和定价优化. 公路交通科技. 2023(05): 228-236 .  百度学术
百度学术
7. 陈月琳,李玉凤. 生鲜农产品社区团购供应链仿真优化. 物流技术. 2023(06): 94-101 .  百度学术
百度学术
8. 潘月,苟欢,毛敏. 考虑消费者新鲜度敏感的O2O生鲜供应链保鲜投入研究. 综合运输. 2023(08): 108-115 .  百度学术
百度学术
9. 魏光兴,梁怡静. 基于成本分担讨价还价的农产品供应链双边保鲜激励. 工业工程. 2023(06): 47-56 .  本站查看
本站查看
10. 薛梅. 消费者具有信息溯源偏好下的区块链成本分担机制探究. 淮北师范大学学报(哲学社会科学版). 2022(02): 71-76 .  百度学术
百度学术
11. 梁薇薇,徐涛,齐佳佳,王玲媛. 乡村振兴视野下考虑公平偏好的农超供应链研究. 全国流通经济. 2022(23): 16-19 .  百度学术
百度学术
其他类型引用(42)



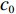
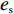
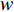
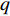
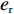
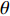
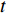
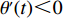
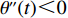
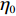
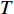
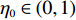
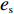
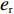
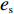
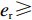
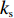
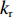
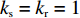
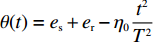
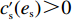
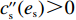
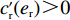
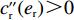
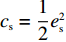
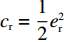
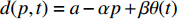
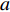
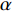
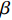
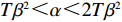
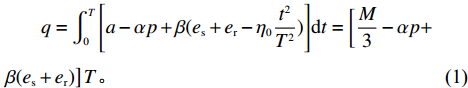
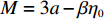
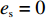
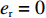
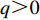
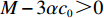
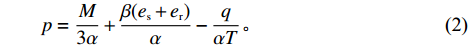
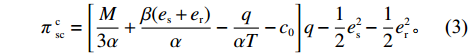
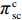
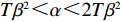
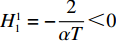
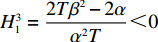
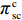
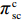
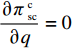
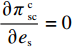
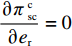
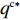
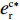
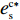




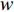
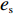
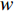
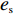
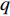
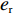

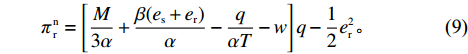
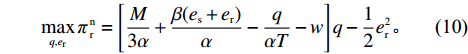
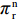
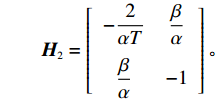
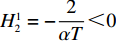
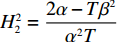
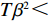
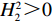
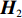
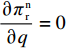
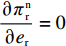
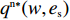
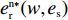
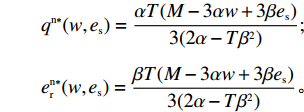
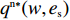
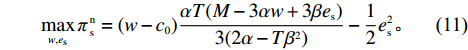
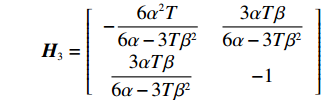
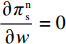
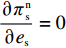
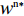
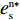
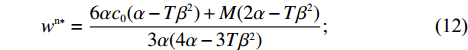



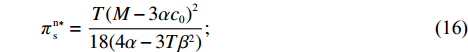
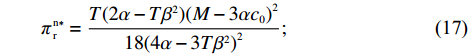
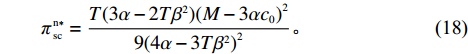

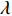
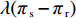
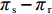
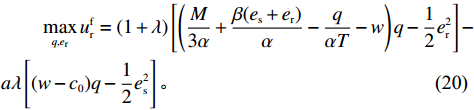
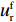
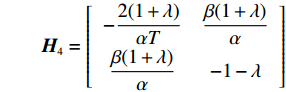
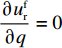
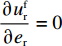
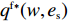
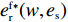
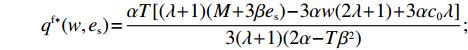
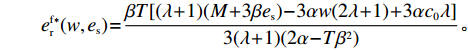

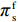
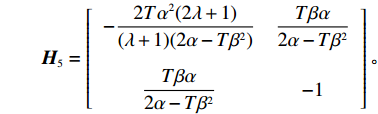
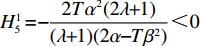
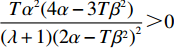
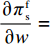
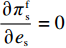
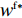
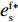
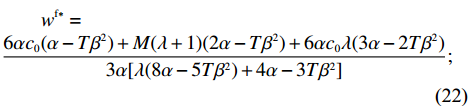
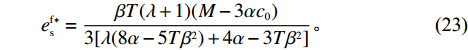
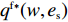
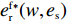
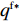
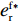
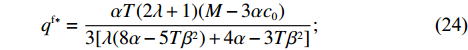
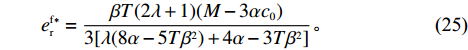
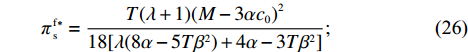
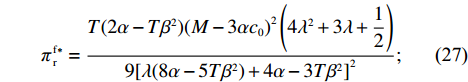
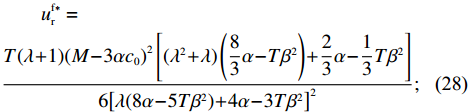
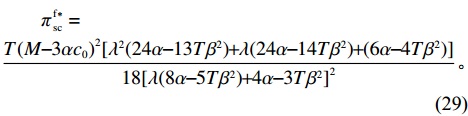
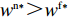
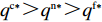
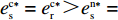
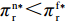
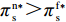
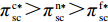
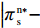
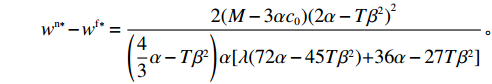
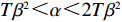
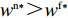
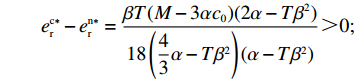
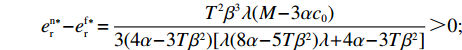
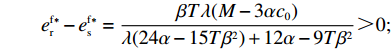
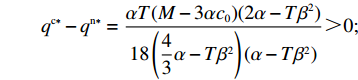
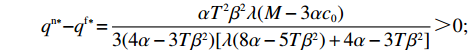
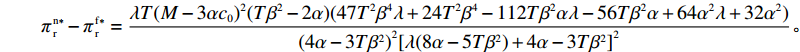
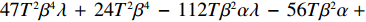
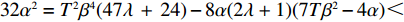
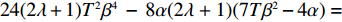
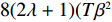
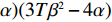
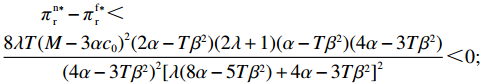
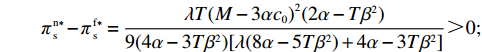
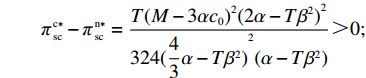
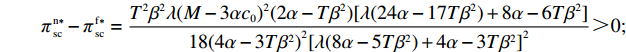
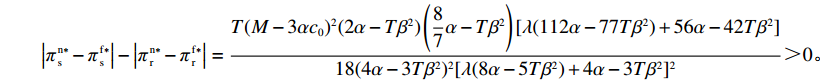
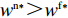
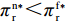
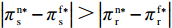
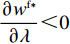
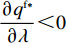
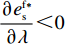
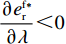
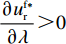
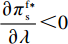
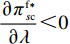
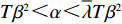
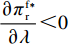
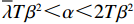
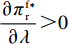
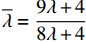
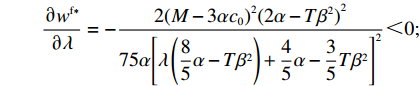
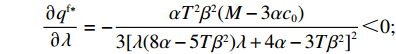
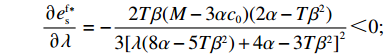
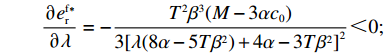
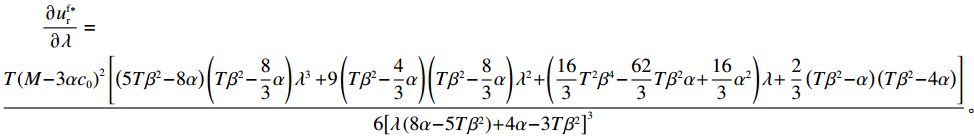
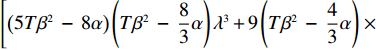
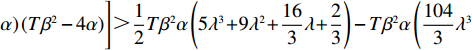
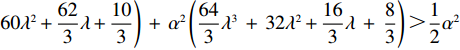
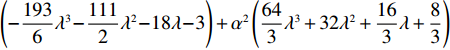
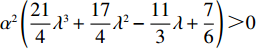
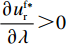
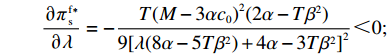
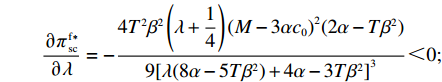

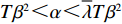
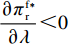
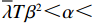
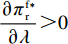
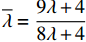
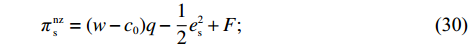
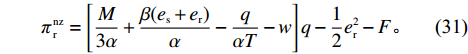

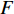
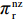
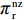
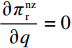
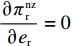
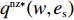
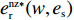
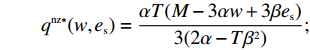
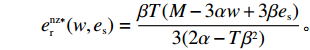
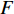
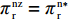
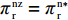
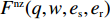
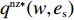
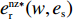
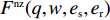
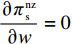
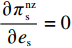
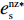
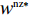


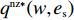
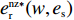
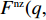
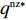
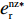
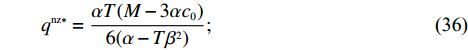
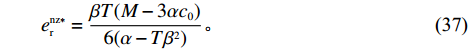
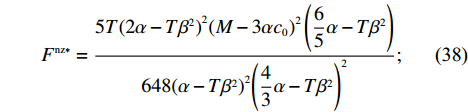
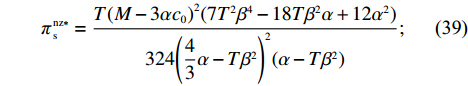
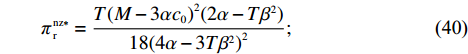
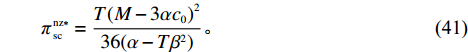
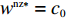
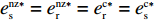
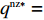
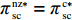
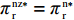
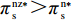
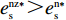
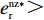
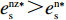
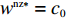
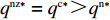
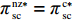
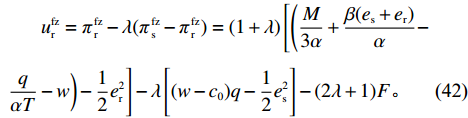
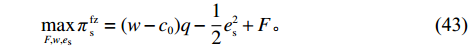



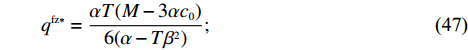

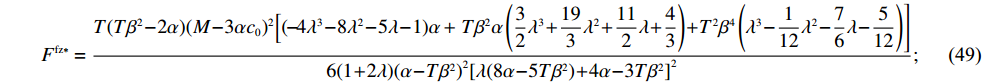
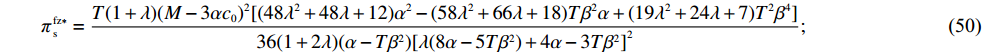
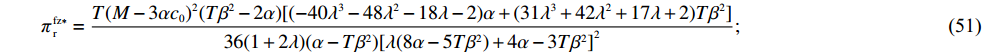
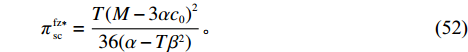
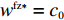
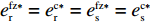
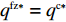
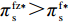
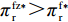
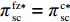
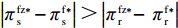
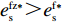
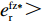
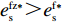
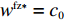
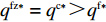
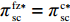
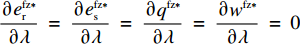
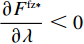
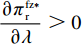
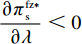
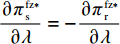
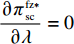
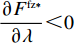
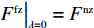
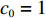
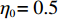
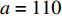
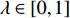
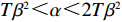
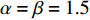
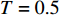
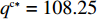
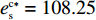
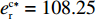
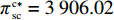
 下载:
下载: