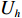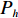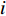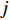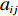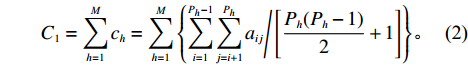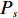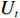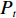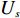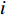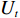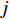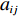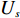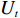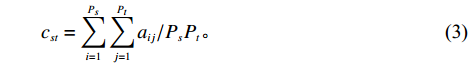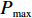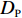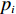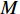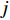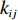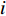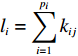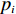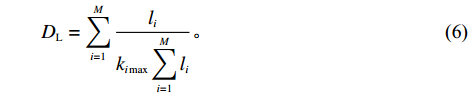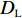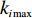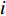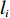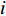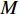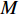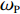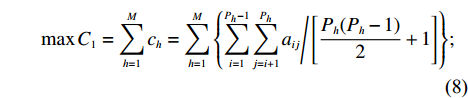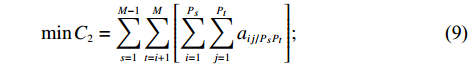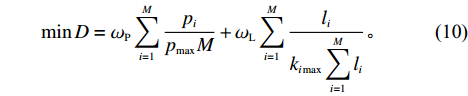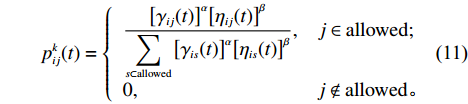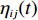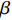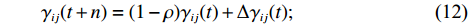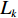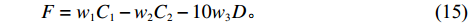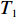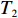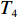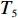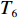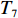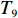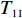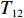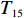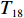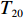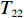Weighted Network Modeling and Module Partitioning Among Crowdsourcing Design Tasks for Social Product Development
-
摘要:
依据社会化产品开发众包设计任务模块划分的需要,针对产品原子设计任务之间关联的含糊性,采用11级标度加权网络来描述它们的关系并进行剪枝的原理与方法。以模块内聚合度最大、模块间耦合度最小、协作设计难度最低为目标函数,建立产品社会化设计众包任务模块划分的优化模型,采用蚁群算法进行求解;论述原子设计任务之间在功能和结构上信息交流相关度、承包方协作难度的计算方法,给出众包任务模块划分的原则、步骤,并举实例说明所提出方法的可行性。
Abstract:According to the needs of module division for crowdsourcing design tasks under social product development and aiming at the ambiguity of the correlation among product atomic design tasks, the elementary theory and methods that an 11-level scale weighted networks was used to describe their relationships, and then the weighted network was pruned. An optimization model of module division of crowdsourcing tasks under social design was established with the objective function of maximizing the degree of aggregation within the module, and minimizing the coupling degree between modules, and minimizing the difficulty of collaborative design, and an ant colony algorithm was used to solve it. The calculation methods of relevance of functional and structural information exchange among atomic design tasks and of the difficulty of contractor cooperation were discussed. The principles and steps of crowdsourcing task module division were given. Examples were given to illustrate the feasibility of the proposed method.
-
社会化产品开发(social product development, SPD)[1]借助社会化的计算技术、工具和媒体,为充分利用企业及社会上的人才、技术和资源等,进行开放式创新创造了机遇。而采用众包(crowdsourcing)[2]技术进行设计是SPD的主要特征之一,称之为众包设计[3]。
当代产品一般比较复杂,采用众包设计方式时,需要将总设计任务划分为若干子任务,通过众包平台分配給合适的承包方,便于设计工作顺利开展。因此,产品众包设计任务模块的合理划分,就成为了众包式社会化产品开发过程的首要关键问题[1,3-4]。
一般来说,产品众包设计任务模块的划分,首先采用功能分解法和结构分解法,进行产品任务分解[5]。然后,采用设计结构矩阵(design structure matrix, DSM)[6]及其改进的区间数设计结构矩阵IDSM[7]和模糊设计结构矩阵FDSM[8]等对产品零部件的原子设计任务之间的关系进行描述;再依据原子设计任务之间的关系的紧密度,按一定的规则进行重组,得到产品设计的若干任务模块。最后,对这些任务模块进行描述,包装构成相应的产品众包设计任务。
由于DSM的直观性不强,人们寻找其他方法来描述原子设计任务间关系。最常采用的是图论的方法,如Duin等[9]和胡从林等[10]用有向图表示原子设计任务间关系,从有向图中得到各原子设计任务间的可达矩阵,再由可达矩阵对原子设计任务进行耦合聚类划分为若干任务模块。陈健等[11]采用权重有向图表示原子设计任务间信息交互的强弱关系,并将原子设计任务信息交互强弱关系定量地映射转化为设计结构矩阵DSM,再由DSM计算得出各原子设计任务间耦合关系,并重组为若干任务模块。
采用图论法来描述原子设计任务之间的关系,直观明了,易于理解。但是,目前还是要转化为可达矩阵或设计结构矩阵等;并与采用设计结构矩阵及其改进形式描述原子设计任务之间的关系一样,最终都要计算转为各原子设计任务间的定量耦合关系,由此来进行聚类重组为任务模块。
众所周知,对于产品开发,尤其是新产品的设计或对现有产品的改型设计,原子设计任务之间的关系、信息交流程度难以准确把握,常具有含糊性。本文研究采用11级标度加权网络来描述其关系,主要依据任务模块内聚合度、模块间耦合度、协作设计难度等对原子设计任务进行聚类,重组为若干众包设计任务模块。
1. 基于加权网络的产品众包设计任务关系建模与模块划分方法
1.1 划分产品众包设计任务模块原则与过程
现代产品变得越来越复杂,在社会化产品开发中,复杂的产品常分解为数量合理、功能独立和结构完整的模块。而采用众包设计时,需要适当控制任务模块的粒度,以便能顺利地由设计方接受。
根据产品模块的定义和社会化开发模式的特点,众包设计任务模块划分原则可确定为满足该产品模块功能独立性和结构完整性;众包设计任务模块内的原子设计任务间信息交流聚合度尽量大,模块间信息交流耦合度尽可能小,且协作设计难度尽量低[7]。
因此,社会化产品开发中众包设计任务模块划分的主要步骤如下。
1) 按功能结构信息交流程度,把产品分解成若干基本单元或称为零部件,并将这些零部件的设计设为原子设计任务。
2) 按功能和结构关联,计算产品零部件相关度;并以原子设计任务为节点、产品零部件相关度为边,构造描述原子设计任务之间关系的加权网络。
3) 按各种的粒度,对上述加权网络进行剪枝,形成若干任务模块划分方案;并计算各个方案中各模块内的聚合度、模块之间的耦合度、协作设计的难度。
4) 根据产品众包设计任务模块划分原则,建立模块划分的优化模型;并应用智能算法求解该模型,得到最终的任务划分方案。
其中,第1) 步要满足产品模块的功能独立性和结构完整性,这相对简单也较成熟。本文重点研究后面3个步骤的实现方法。
1.2 原子设计任务之间关系的加权网络描述
1.2.1 原子设计任务之间的相关度
产品零部件或基本单元存在功能和结构方面的关联。其中,功能上的关联主要体现在功能接口的能量流、物料流和信息流(包括机电信号和作用力等信息交互)的传递上;而结构上的关联主要体现在接触、联接和配合的空间和几何接口关系上。
通过相关性分析方法得到产品基本单元两两之间的关联程度,一般很难准确地给出其具体数值。可以根据人的经验和知识进行两两间的比较,用[0,1]区间的11级标度含糊地表示,即为(0, 0.1, 0.2, 0.3,
$ \cdots$ , 0.9, 1.0)中某个值。对于产品基本单元的原子设计任务,它们之间的相关度可由式(1)计算。
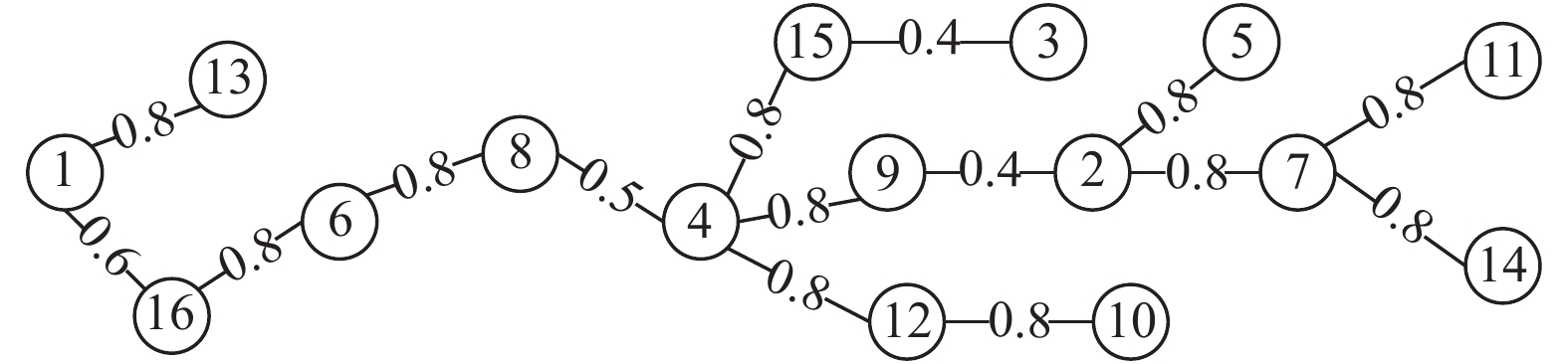
$$\qquad {a_{ij}} = {\omega _{\rm{F}}}{f_{ij}} + {\omega _{\rm{S}}}{s_{ij}}{\text{。}}$$ (1) 其中,
${a_{ij}}$ 、${f_{ij}}$ 和${s_{ij}}$ 分别为两原子设计任务之间的相关度及其基本单元间的功能信息交流相关度、结构信息交流相关度,$i,j = 1,\;2,\; \cdots ,N$ ($N$ 表示产品基本单元的数量);${\omega _{\rm{F}}}$ 和${\omega _{\rm{S}}}$ 为功能关联准则的权重系数和结构关联准则的权重系数,可以根据人类的知识和经验或者使用数学中层次分析法来获得相应权重。1.2.2 原子设计任务间的加权网络
1) 加权网络的构造。
以原子设计任务为节点、它们之间联系为边、信息交流相关度为边的权值,则可以构造原子设计任务间的加权网络,如图1所示。
图1中所示16节点,表示共16个原子设计任务;节点之间连接边上的数字,表示原子设计任务间的信息交流相关度。
2) 加权网络图的剪枝。
按照一定的粒度阈值
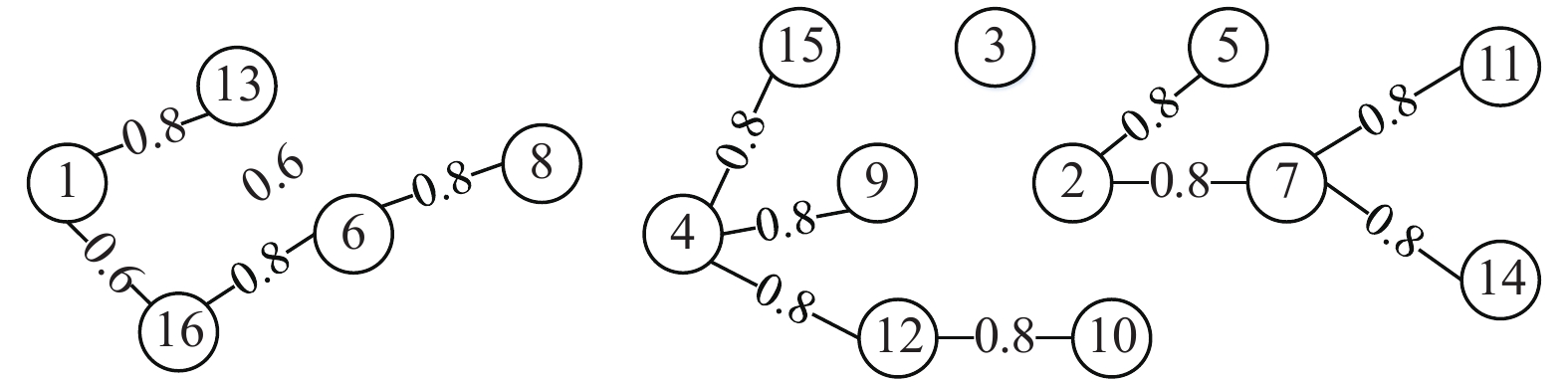
${a_0}$ ,对上述加权图去掉相关度小于${a_0}$ 的边,则得到相应的剪枝图,如图2所示。图2中取粒度阈值
${a_0} = 0.6$ ,剪掉权重小于0.6的连接边后,得到剪枝加权网络图。这表示分为4个任务模块,分别为(1, 6, 8, 13, 16)、(4, 9, 10, 12, 15)、(3)和(2, 5, 7, 11, 14)。1.3 众包设计任务模块内聚合度和模块间耦合度
模块内聚合度是对模块内部基本任务之间相关度的总体描述。设模块
${U_h}$ 有${P_h}$ 个基本任务。由前面的分析知道,任意两个基本任务$i$ 与$j$ 的关联度为${a_{ij}}$ ,则所有$M$ 个模块的总聚合度${C_1}$ 为[12]$$\qquad {C_1} = \displaystyle\sum\limits_{h = 1}^M {{c_h}} = \displaystyle\sum\limits_{h = 1}^M {\left\{ { \displaystyle\sum\limits_{i = 1}^{{P_h} - 1} { \displaystyle\sum\limits_{j = i + 1}^{{P_h}} {{a_{ij}} \Biggr/\left[ {\dfrac{{{P_h}({P_h} - 1)}}{2} + 1} \right]} } } \right\}} {\text{。}}$$ (2) 以同样的思路分析,一个模块与另一个模块的耦合度可以用这个模块内部的基本任务与另一模块内部的基本任务的相关度来描述。假设模块
${U_{{s}}}$ 有${P_{{s}}}$ 个基本任务,模块${U_t}$ 共有${P_t}$ 个基本任务,模块${U_s}$ 内任意一个基本任务$i$ 与模块${U_t}$ 内任意一个基本任务$j$ 的相关度为${a_{ij}}$ ,可以得到模块${U_s}$ 与${U_t}$ 之间的耦合度为[12]$$\qquad {c_{st}} = \displaystyle\sum\limits_{i = 1}^{{P_s}} { \displaystyle\sum\limits_{j = 1}^{{P_t}} {{a_{ij}}} } /{P_s}{P_t}{\text{。}}$$ (3) 则可得所有模块间的总耦合度为
$$\qquad {C_2} = \displaystyle\sum\limits_{s = 1}^{M - 1} { \displaystyle\sum\limits_{t = i + 1}^M {{c_{st}}} }{\text{。}} $$ (4) 1.4 众包设计任务模块协作设计的难度
产品众包设计任务划分为多个模块后,分发给各承包方。若模块包含多个设计任务,则需要由多人组成团队进行协作设计。一般来说,模块规模越大、网络结构越复杂,团队内交流和冲突也越多。所以,协作设计的难度,可用模块规模、网络结构为指标。
1) 模块规模难度。
模块规模用所包含原子设计任务的数目表示。按项目管理知识,团队所含人数越多,越难沟通管理;为使团队有较高的效率,管理者一般对团队总人数有所限制。对应的众包模块内含原子设计任务数量,也应当作同样的限制。所以,在进行加权网络图的剪枝时,假设模块所含原子设计任务的最大数目为
${P_{\max }}$ ,则规模难度指标定义为$$\qquad {D_{\rm{P}}} = \displaystyle\sum\limits_{i = 1}^M {\dfrac{{{p_i}}}{{{P_{\max }}M}}}{\text{。}} $$ (5) 其中,
${D_{\rm{P}}}$ 为规模难度;${p_i}$ 为第$i$ 个模块所含原子设计任务数;$M$ 为模块总数。2) 网络结构难度。
若众包模块存在核心的原子设计任务,则模块内部网络结构特征具有网络中心性(centrality)。通过子图匹配等方式,在寻找到现有的设计团队或即将组建的设计团队中,一般存在具有高中介中心性(betweenness centrality)的节点,是一种“领导者+骨干成员”的团队组织形式。模块的网络中心性越高,则对应的设计团队具有较高的中介中心性的节点越明显,团队内协作和冲突消解的难度也就越低。
模块
$i$ 的网络内节点$j$ 的连接程度用其度${k_{ij}}$ [13]表示,它是与该节点连接的其他节点的数目,则模块$i$ 的网络总度数为${l_i} = \displaystyle\sum\limits_{i = 1}^{{p_i}} {{k_{ij}}} $ ,${p_i}$ 为第$i$ 个模块所含原子设计任务数,因此,结构难度指标定义为$$\qquad {D_{\rm{L}}} = \displaystyle\sum\limits_{i = 1}^M {\dfrac{{{l_i}}}{{{k_{i\max }} \displaystyle\sum\limits_{i = 1}^M {{l_i}} }}}{\text{。}} $$ (6) 其中,
${D_{\rm{L}}}$ 为结构难度;${k_{i\max }}$ 为模块$i$ 的网络内节点的最大度;${l_i}$ 为第$i$ 个模块网络总度数;$M$ 为模块总数。产品划分为
$M$ 个模块后的总匹配难度为$$\qquad D = {\omega _{\rm{P}}}{D_{\rm{P}}} + {\omega _{\rm{L}}}{D_{\rm{L}}}{\text{。}}$$ (7) 其中,
${\omega _{\rm{P}}}$ 和${\omega _{\rm{L}}}$ 为模块规模难度指标的权重系数和链接难度指标的权重系数,可以根据人类的知识和经验或者使用数学中层次分析法来获得相应权重。2. 产品众包设计任务模块划分的优化
2.1 产品众包设计任务模块划分的优化模型
根据产品众包设计任务划分的原则,模块内部信息交流的聚合度最大,模块之间的信息交流耦合度最小,且任务协作的难度最低。则产品众包设计任务划分的优化模型为
$$\qquad \max {C_1} = \displaystyle\sum\limits_{h = 1}^M {{c_h}} = \displaystyle\sum\limits_{h = 1}^M {\left\{ { \displaystyle\sum\limits_{i = 1}^{{P_h} - 1} { \displaystyle\sum\limits_{j = i + 1}^{{P_h}} {{a_{ij}}\Biggr/\left[ {\dfrac{{{P_h}({P_h} - 1)}}{2} + 1} \right]} } } \right\}} ;$$ (8) $$\qquad \min {C_2} = \displaystyle\sum\limits_{s = 1}^{M - 1} { \displaystyle\sum\limits_{t = i + 1}^M {\left[ { \displaystyle\sum\limits_{i = 1}^{{P_s}} { \displaystyle\sum\limits_{j = 1}^{{P_t}} {{a_{ij/{P_{{s}}}{P_t}}}} } } \right]} } ;$$ (9) $$\qquad \min D = {\omega _{\rm{P}}} \displaystyle\sum\limits_{i = 1}^M {\dfrac{{{p_i}}}{{{p_{\max }}M}}} + {\omega _{\rm{L}}} \displaystyle\sum\limits_{i = 1}^M {\dfrac{{{l_i}}}{{{k_{i\max }} \displaystyle\sum\limits_{i = 1}^M {{l_i}} }}} {\text{。}}$$ (10) 2.2 产品众包设计任务划分模型的求解
任务模块划分属于典型的组合最优化问题,是NP-Hard问题,适宜采用智能的蚁群算法求解。
步骤1 初始化各个参数以及矩阵值,蚂蚁数,迭代次数,初始化信息素;存储好功能结构信息交流相关值。
步骤2 迭代开始。
步骤3 把蚂蚁随机放在各个顶点上,相关数据做好记录。
步骤4 按式(11),选择转移概率最大的那个作为下一个选择,如果所得的转移概率大于rand(),则归为上一个顶点所属模块,否则作为另一模块。
$$\begin{split} \qquad p_{ij}^k(t) = \left\{ {\begin{array}{l} {\dfrac{{{{\left[ {{\gamma _{ij}}(t)} \right]}^\alpha }{{\left[ {{\eta _{ij}}(t)} \right]}^\beta }}}{{ \displaystyle\sum\limits_{s \subset {\rm{allowed}}} {{{\left[ {{\gamma _{is}}(t)} \right]}^\alpha }{{\left[ {{\eta _{is}}(t)} \right]}^\beta }} }},} \quad{j \in {\rm{allowed;}}}\\ {0,}\qquad\qquad\qquad\qquad \quad {j \notin {\rm{allowed}}{\text{。}}} \end{array}} \right. \end{split} $$ (11) 其中,
${\gamma _{ij}}(t)$ 表示顶点信息素;${\eta _{ij}}(t)$ 表示顶点功能结构信息交流相关性;$\alpha $ 为信息素启发因子;$\beta $ 为相关性启发因子。步骤5 如果每只蚂蚁所有顶点还没有访问完,则继续步骤3;否则步骤6。
步骤6 更新信息素,根据模块划分递增表所走过的路径,按照式(12) ~ (14)对称添加信息素。
$$\qquad {\gamma _{ij}}(t + n) = (1 - \rho ){\gamma _{ij}}(t) + \Delta {\gamma _{ij}}(t);$$ (12) $$\qquad \Delta {\gamma _{ij}}(t) = \displaystyle\sum\limits_{k = 1}^m {\Delta \gamma _{ij}^k(t)} ;$$ (13) $$\qquad \Delta \gamma _{ij}^k = \left\{ \begin{array}{l} {Q/{L_k}}; \\ 0 {\text{。}} \end{array} \right.$$ (14) 其中,
$Q$ 为常量;${L_k}$ 是蚂蚁在本次循环中获得模块划分适应度值,其适应度值按照式(15)计算,同时保留适应度最高的那个值以及模块划分。$$\qquad F = {w_1}{C_1} - {w_2}{C_2} - 10{w_3}D{\text{。}}$$ (15) 步骤7 迭代次数未完则转步骤2,否则结束,输出最优解。
3. 实例分析
3.1 问题描述
以ZL50型轮式装载机工作装置为例[14],其设计所含基本任务为1-铲斗,2-螺栓,3、20-垫圈,4-摇臂销轴,5-动臂,6-中摇臂销轴,7、10、15、27-密封圈,8-摇臂钢套,9-动臂钢套,11-拉杆,12-齿套,13-斗齿固定销,14-卡圈,16-拉杆钢套,17-动臂上钢套,18-油杯,19-螺栓,21-摇臂,22-垫片,23-铲斗钢套,24-铲斗小销轴,25-铲斗上销轴,26-摇臂上销轴,27-定位环;分别用字母
${T_1}$ 、${T_2}$ 、${T_3}$ 、${T_4}$ 、${T_5}$ 、${T_6}$ 、${T_7}$ 、${T_8}$ 、${T_9}$ 、${T_{10}}$ 、${T_{11}}$ 、${T_{12}}$ 、${T_{13}}$ 、${T_{14}}$ 、${T_{15}}$ 、${T_{16}}$ 、${T_{17}}$ 、${T_{18}}$ 、${T_{19}}$ 、${T_{20}}$ 、${T_{21}}$ 、${T_{22}}$ 、${T_{23}}$ 、${T_{24}}$ 、${T_{25}}$ 、${T_{26}}$ 、${T_{27}}$ 表示。相应的基本任务功能信息交流相关度和结构信息交流相关度如表1所示,分别对应上下三角形数值,其中空白之处数值为0或者是经过前期处理信息交流相关度忽略不计。表 1 信息交流相关度Table 1. Relevance of information exchange${T_1}$ ${T_2}$ ${T_3}$ ${T_4}$ ${T_5}$ ${T_6}$ ${T_7}$ ${T_8}$ ${T_9}$ ${T_{10}}$ ${T_{11}}$ ${T_{12}}$ ${T_{13}}$ ${T_{14}}$ ${T_{15}}$ ${T_{16}}$ ${T_{17}}$ ${T_{18}}$ ${T_{19}}$ ${T_{20}}$ ${T_{21}}$ ${T_{22}}$ ${T_{23}}$ ${T_{24}}$ ${T_{25}}$ ${T_{26}}$ ${T_{27}}$ ${T_1}$ 1 0.6 0.8 0.7 0.9 ${T_2}$ 0.7 1 0.6 0.5 0.7 ${T_3}$ 0.6 0.5 1 0.5 0.6 ${T_4}$ 1 0.6 0.8 0.6 0.7 ${T_5}$ 1 0.6 0.6 0.7 0.6 0.5 0.5 0.7 0.7 0.6 ${T_6}$ 0.6 1 0.5 0.7 0.6 0.7 0.8 0.5 0.6 0.6 ${T_7}$ 0.7 1 0.6 0.6 0.7 ${T_8}$ 0.5 0.7 1 0.7 0.9 ${T_9}$ 0.6 0.6 1 0.8 0.8 0.8 0.7 0.7 0.9 0.7 ${T_{10}}$ 0.6 0.7 0.6 1 0.5 0.6 0.8 0.6 0.6 0.6 ${T_{11}}$ 1 0.7 0.5 ${T_{12}}$ 1 0.6 0.5 ${T_{13}}$ 0.7 1 0.8 ${T_{14}}$ 0.6 0.7 1 ${T_{15}}$ 0.6 1 0.7 ${T_{16}}$ 0.8 0.6 1 ${T_{17}}$ 0.6 0.6 0.6 0.7 1 0.5 0.6 0.7 0.7 0.8 ${T_{18}}$ 1 ${T_{19}}$ 0.5 0.6 0.6 0.6 0.6 1 0.6 0.5 0.9 0.8 ${T_{20}}$ 0.6 0.6 0.5 0.8 0.7 0.5 1 0.8 0.8 0.7 ${T_{21}}$ 0.6 0.6 0.7 1 0.5 ${T_{22}}$ 0.6 0.7 0.6 0.6 0.7 0.6 0.7 1 0.6 0.7 ${T_{23}}$ 0.7 0.7 0.6 0.6 0.9 0.8 0.9 0.5 1 0.8 ${T_{24}}$ 0.6 0.7 0.5 1 0.7 ${T_{25}}$ 0.6 0.8 0.9 0.6 1 ${T_{26}}$ 0.6 0.8 0.8 0.7 1 ${T_{27}}$ 0.5 0.9 0.6 0.8 0.7 0.8 0.8 0.9 0.6 1 3.2 实验数据
采用C语言编写程序,迭代次数均为
1000 次,设置不同的参数,实验结果如表2所示。表 2 实验结果Table 2. The experimental results参数设置 迭代次数 最优模块划分 最优适应度值 α = 4
β = 2
Q = 10
Μ = 15
ρ = 0.21 2,1,2,10,9,8,10,10,9,7,12,13,13,
13,12,12,6,11,9,4,10,3,5,2,2,10,3− 27.4000 2- 1000 3,3,3,1,2,2,1,1,2,2,5,6,6,
6,5,5,2,4,2,2,1,2,2,3,3,1,291.4000 α = 3
β = 5
Q = 20
Μ = 20
ρ = 0.51 9,10,9,8,4,3,8,6,4,3,12,1,1,1,
12,12,3,11,4,3,7,3,3,10,9,5,2− 15.0000 2- 1000 3,3,3,1,2,2,1,1,2,2,5,6,6,
6,5,5,2,4,2,2,1,2,2,3,3,1,291.4000 4. 结束语
通过两次实验,结果趋于快速稳定,
1000 次迭代后,共有6个不同的数字,故该装置可划分为6个模块,其中相同数字划分为同一模块,不同数字归属不同模块,得到装载机工作装置的模块划分结果:铲斗模块 (T1、T2、T3、T24、T25)、斗齿模块 (T12、T13、T14)、动臂模块 (T5、T6、T9、T10、T17、T19、T20、T22、T23、T27)、摇臂模块 (T4、T7、T8、T21、T26)、拉杆模块 (T11、T15、T16)和油杯组模块 (T18),得到模块划分与论文[14]结果相同,证实本文方法的可行性。社会化产品开发众包设计任务模块划分,是适应当前形势的一种任务分配模式。蚁群算法具备收敛速度极快特点,在机械时效性方面具备一定优势。随着众包任务设计的复杂性增加,云计算大数据的软硬件技术支撑,互联网 + 众包任务分配必将更智能更科学合理。下一步作者将引入pareto最优解寻求更合理的多目标解,同时将更复杂的任务分配纳入作者的研究当中。
-
表 1 信息交流相关度
Table 1 Relevance of information exchange
T1 T2 T3 T4 T5 T6 T7 T8 T9 T10 T11 T12 T13 T14 T15 T16 T17 T18 T19 T20 T21 T22 T23 T24 T25 T26 T27 T1 1 0.6 0.8 0.7 0.9 T2 0.7 1 0.6 0.5 0.7 T3 0.6 0.5 1 0.5 0.6 T4 1 0.6 0.8 0.6 0.7 T5 1 0.6 0.6 0.7 0.6 0.5 0.5 0.7 0.7 0.6 T6 0.6 1 0.5 0.7 0.6 0.7 0.8 0.5 0.6 0.6 T7 0.7 1 0.6 0.6 0.7 T8 0.5 0.7 1 0.7 0.9 T9 0.6 0.6 1 0.8 0.8 0.8 0.7 0.7 0.9 0.7 T10 0.6 0.7 0.6 1 0.5 0.6 0.8 0.6 0.6 0.6 T11 1 0.7 0.5 T12 1 0.6 0.5 T13 0.7 1 0.8 T14 0.6 0.7 1 T15 0.6 1 0.7 T16 0.8 0.6 1 T17 0.6 0.6 0.6 0.7 1 0.5 0.6 0.7 0.7 0.8 T18 1 T19 0.5 0.6 0.6 0.6 0.6 1 0.6 0.5 0.9 0.8 T20 0.6 0.6 0.5 0.8 0.7 0.5 1 0.8 0.8 0.7 T21 0.6 0.6 0.7 1 0.5 T22 0.6 0.7 0.6 0.6 0.7 0.6 0.7 1 0.6 0.7 T23 0.7 0.7 0.6 0.6 0.9 0.8 0.9 0.5 1 0.8 T24 0.6 0.7 0.5 1 0.7 T25 0.6 0.8 0.9 0.6 1 T26 0.6 0.8 0.8 0.7 1 T27 0.5 0.9 0.6 0.8 0.7 0.8 0.8 0.9 0.6 1 表 2 实验结果
Table 2 The experimental results
参数设置 迭代次数 最优模块划分 最优适应度值 α = 4
β = 2
Q = 10
Μ = 15
ρ = 0.21 2,1,2,10,9,8,10,10,9,7,12,13,13,
13,12,12,6,11,9,4,10,3,5,2,2,10,3− 27.4000 2- 1000 3,3,3,1,2,2,1,1,2,2,5,6,6,
6,5,5,2,4,2,2,1,2,2,3,3,1,291.4000 α = 3
β = 5
Q = 20
Μ = 20
ρ = 0.51 9,10,9,8,4,3,8,6,4,3,12,1,1,1,
12,12,3,11,4,3,7,3,3,10,9,5,2− 15.0000 2- 1000 3,3,3,1,2,2,1,1,2,2,5,6,6,
6,5,5,2,4,2,2,1,2,2,3,3,1,291.4000 -
[1] PETERSON A, SCHAEFER D. Social product development: introduction, overview, and current status[M]//SCHAEFER D. Product development in the socio-sphere. Switzerland: Springer, 2014: 1-33.
[2] SCHAEFER D. Industrial game changers for the socio-sphere[R/OL]. (2012-01). https://researchportal.bath.ac.uk/en/publications/industrial-game-changers-for-the-socio-sphere.
[3] 张富强, 江平宇, 郭威. 服务型制造学术研究与工业应用综述[J]. 中国机械工程, 2018, 29(18): 2144-2163. ZHANG Fuqiang, JIANG Pingyu, GUO Wei. Academic research and industrial application of service-oriented manufacturing[J]. China Mechanical Engineering, 2018, 29(18): 2144-2163.
[4] 严杰, 刘人境, 刘晗. 国内外众包研究综述[J]. 中国科技论坛, 2017, 21(8): 59-68. YAN Jie, LIU Renjing, LIU Han. A literature review of domestic and foreign crowdsourcing research[J]. Forum on Science and Technology in China, 2017, 21(8): 59-68.
[5] 李刚炎, 肖佩, 杨明忠. 机械设计分解方法的研究及其应用[J]. 武汉汽车工业大学学报, 1997, 19(4): 27-30. LI Gangyan, XIAO Pei, YANG Mingzhong. Study of decomposition methods in mechanical design and application[J]. Journal of Wuhan Automotive Polytechnic University, 1997, 19(4): 27-30.
[6] 李靓, 武健伟, 石浩然. 基于DSM的耦合模块划分方法的研究[J]. 机械设计与制造, 2008, 46(8): 223-225. DOI: 10.3969/j.issn.1001-3997.2008.08.090 LI Jing, WU Jianwei, SHI Haoran. Research on the improved dsm arthmetic for coupling task order programming[J]. Machinery Design & Manufacture, 2008, 46(8): 223-225. DOI: 10.3969/j.issn.1001-3997.2008.08.090
[7] 刘电霆, 周德俭. 基于区间数设计结构矩阵的任务分解与重组[J]. 机械设计与研究, 2009, 25(6): 7-9. LIU Dianting, ZHOU Dejian. Task decomposition & recombination design structure matrix based on interval number[J]. Machine Design and Research, 2009, 25(6): 7-9.
[8] 涂建伟, 李彦, 李文强, 等. 基于FDSM的产品族设计模块化方法的研究[J]. 组合机床与自动化加工技术, 2011, 53(8): 16-20. TU Jianwei, LI Yan, LI Wenqiang, et al. Method for product family modular design based on fuzzy design structure matrix[J]. Modular Machine Tool & Automatic Manufacturing Technique, 2011, 53(8): 16-20.
[9] DUIN H, ESCHENBACHER J, THOBEN K D. Modeling dynamics in collaboration: an extension to the collaborative network relationship analysis[C]// Proceedings of 12th IFIP WG 5.5 Working Conference on Virtual Enterprises. Brazil: São Paulo, 2011: 287-294.
[10] 胡从林, 容芷君, 陈奎生, 等. 产品设计任务的聚类优化研究[J]. 机械设计与制造, 2014, 52(7): 259-261. DOI: 10.3969/j.issn.1001-3997.2014.07.079 HU Conglin, RONG Zhijun, CHEN Kuisheng, et al. Research on clustering optimization of product design task[J]. Machinery Design & Manufacture, 2014, 52(7): 259-261. DOI: 10.3969/j.issn.1001-3997.2014.07.079
[11] 陈健, 莫蓉, 初建杰, 等. 工业设计云服务平台协同任务模块化重组与分配方法[J]. 计算机集成制造系统, 2018, 24(3): 720-930. CHEN Jian, MO Rong, CHU Jianjie, et al. Modular restructuring and distribution method of collaborative task in industrial design cloud platform[J]. Computer Integrated Manufacturing Systems, 2018, 24(3): 720-930.
[12] 刘电霆, 胡浩平. 绿色产品模块划分的不确定优化及求解[J]. 科技通报, 2015, 31(11): 143-147. DOI: 10.3969/j.issn.1001-7119.2015.11.030 LIU Dianting, HU Haoping. Uncertain optimization and solution of green product module partition[J]. Bulletin of Science and Technology, 2015, 31(11): 143-147. DOI: 10.3969/j.issn.1001-7119.2015.11.030
[13] 汪小帆, 李翔, 陈关荣. 复杂网络理论及其应用[M]. 北京: 清华大学出版社, 2006. [14] 谌炎辉, 周德俭, 袁海英, 等. 复杂产品的最小最大划分模块化方法[J]. 计算机集成制造系统, 2012, 18(1): 9-14. CHEN Yanhui, ZHOU Dejian, YUAN Haiying, et al. Min-max partition modularity method of complex product[J]. Computer Integrated Manufacturing Systems, 2012, 18(1): 9-14.
-
期刊类型引用(3)
1. 王北海,吴云迪,姚成汉. 面向固定条盒自动装填设备协同设计的任务规划研究. 包装工程. 2023(03): 172-178 .  百度学术
百度学术
2. 张旭,李晨辉,许彤,白仲航. 设计任务驱动的工具类产品创新. 科学技术与工程. 2023(11): 4623-4637 .  百度学术
百度学术
3. 隋蕙名. “互联网+”产品设计开发的众创模式分析. 互联网周刊. 2023(13): 45-47 .  百度学术
百度学术
其他类型引用(3)





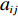
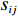
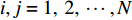
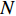
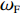
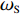
 下载:
下载: