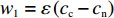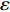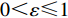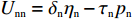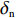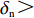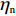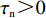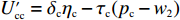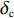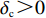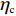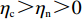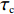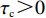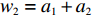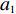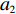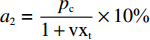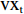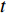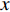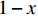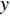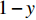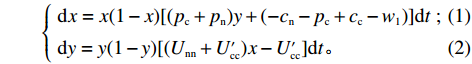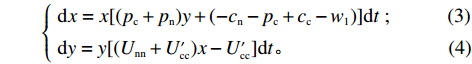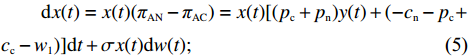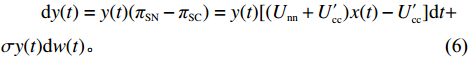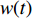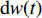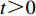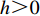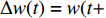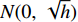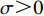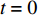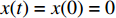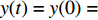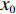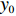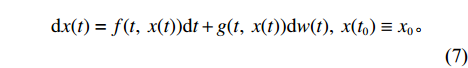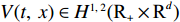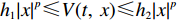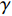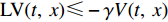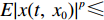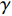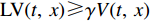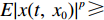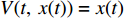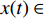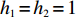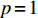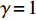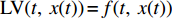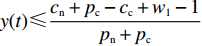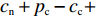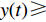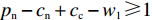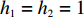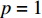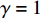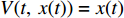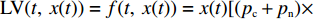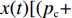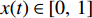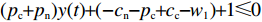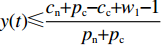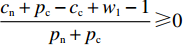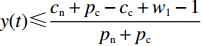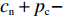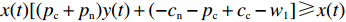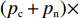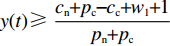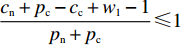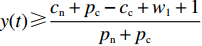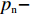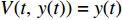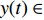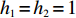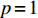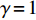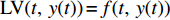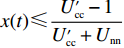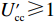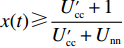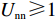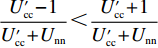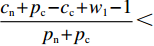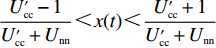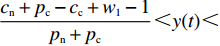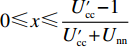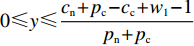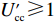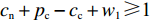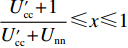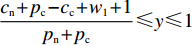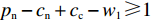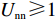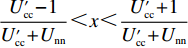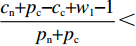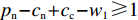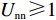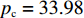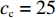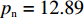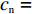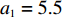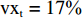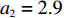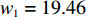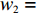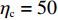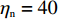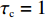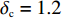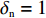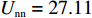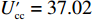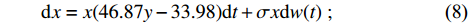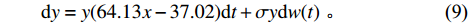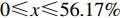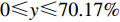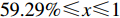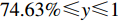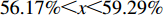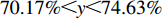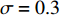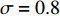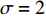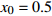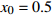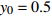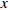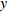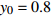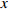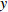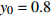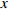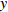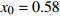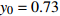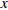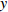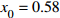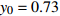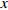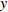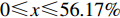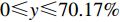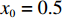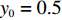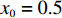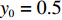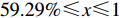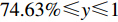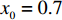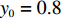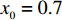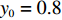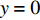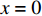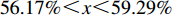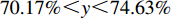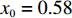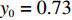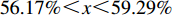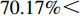A Simulation Analysis of Low-carbon Diffusion Stability in Heterogeneous Agents Based on Stochastic Evolutionary Game
-
摘要:
为了分析不确定性因素对异质性主体中低碳扩散过程的影响,构建以企业和消费者为主体的随机演化博弈模型,并对其进行稳定性分析,得到3种低碳扩散稳定情形,且以新能源汽车比亚迪E6为例进行仿真验证。研究结果表明,当采取低碳策略的企业比例和采取低碳消费的消费者比例较低时,在不同的噪声强度下,低碳扩散最终都不能实现有效稳定;随着两者比例的增大,在经历混沌状态后,低碳策略和低碳消费能分别在企业和消费者中成功扩散,且在不同噪声强度下实现有效稳定。
Abstract:In order to analyze the influence of uncertain factors on low-carbon diffusion in heterogeneous agents, a stochastic evolutionary game model was constructed considering enterprises and consumers, the stability of this model analyzed, and the corresponding three stability scenarios presented. Moreover, the scenarios were simulated and verified through an example of new energy vehicle BYD E6. The research results show that when the proportions of enterprises with low-carbon strategy and consumers with low-carbon consumption are small, the success of low-carbon diffusion cannot be realized no matter what the noise intensity is, and with the above two proportions increasing, low-carbon strategy and low-carbon consumption can diffuse successfully in enterprises and consumers respectively, and low-carbon diffusion can arrive at effective stability successfully under different noise intensities, after experiencing a chaotic state.
-
Keywords:
- low-carbon diffusion /
- stability /
- heterogeneous agents /
- stochastic evolutionary game /
- noise
-
低碳发展是一种被广泛认可的解决环境问题的途径。为了实现低碳发展,需要低碳理念、低碳知识、低碳技术、低碳策略在各个领域和行业的扩散。低碳扩散过程不仅仅涉及人、财、物方面,也涉及到多个参与者(政府、企业、消费者等),同时存在宏观政策、行业环境等不确定性因素,这些不确定性因素会对低碳扩散过程的稳定性产生影响。
目前,关于低碳扩散的研究主要集中在以下3方面。1) 低碳扩散的影响因素研究[1-5]。主要包括低碳技术扩散的影响因素[1-2]和低碳技术创新扩散的影响因素[3-5]两类。例如,Li等[2]以
1115 家种米农户为例,实证分析影响低碳农业技术扩散的因素。Lai等[3]运用系统动力学和问卷调查法分析建筑行业中低碳技术创新扩散的影响因素。徐莹莹等[5]通过建立市场机制和政府规制下潜在采纳企业的低碳技术创新采纳决策及扩散模型,研究网络规模、规制手段等因素对宏观扩散的影响。2) 低碳扩散的模型及优化研究[6-9]。Kumar等[6]建立能源系统的空间技术扩散优化模型。袭希等[9]运用逾渗模型研究低碳技术在市场中的扩散原理。3) 低碳扩散的内部机制研究[10-11]。例如,付秋芳等[10]针对在碳减排投入中供应商或制造商的“搭便车”行为问题,分析契约和惩罚机制下的演化博弈结果。吕希琛等[11]分析环境规制下制造业企业低碳技术扩散的动力机制。综上所述,相关研究主要有以下研究动态。首先就研究内容而言,学者多是从低碳技术扩散的角度展开研究,但是低碳技术和低碳扩散并不能完全等同,低碳技术扩散主要是指以企业为主体展开的相关分析,而低碳扩散不仅包括低碳技术在企业中的扩散,还包括低碳产品在消费者中的扩散,因此仅仅从低碳技术角度分析低碳扩散的影响及效果是不完备的,有必要考虑低碳产品在消费者中的扩散效果。鲜少有文献对低碳扩散的稳定性进行研究。稳定性概念源自物理学和生态学[12-13],缺乏稳定的系统是没有效率的,由企业和消费者构成的低碳扩散系统也不例外。因此,研究低碳扩散的稳定性对于低碳扩散效果的评估和可持续发展具有重要的意义。其次,就研究方法而言,与低碳扩散有关的研究模型多采用动力学模型和确定性的演化博弈模型,较少有文献考虑随机演化博弈模型。随机演化博弈模型是把博弈理论分析和动态演化过程分析结合起来的一种理论。它不同于博弈论将重点放在静态均衡和比较静态均衡上,强调的是一种动态的均衡。目前,随机演化博弈理论已经运用到群体行为控制[14]、农业[15]等多种领域,其中,也不乏有文献对相关问题的稳定性进行分析[15]。但是运用随机演化博弈方法研究异质性主体中的低碳扩散稳定性问题,却鲜有文献涉及。
为此,基于现有的理论和文献,本文运用随机演化博弈方法研究异质性主体中低碳扩散的稳定性问题。基于构建的以企业和消费者为主体的确定性演化博弈模型,建立随机演化博弈模型,并对该模型进行稳定性分析,获得3种低碳扩散稳定情形,且以新能源汽车比亚迪E6为例对上述内容进行仿真验证分析,提出相关政策建议。
1. 模型与方法
1.1 符号说明与假设
本文给出如下假设。
假设1 低碳策略对应的低碳产品的价格为
${p_{\rm{c}}}$ ,非低碳策略对应的产品价格为$ {p_{\rm{n}}} $ ,且$ {p_{\rm{c}}} >{p_{\rm{n}}} >0 $ 。假设2 采取低碳策略的企业单位低碳产品成本为
$ {c_{\rm{c}}} $ ,采取非低碳策略的企业单位产品成本为$ {c_{\rm{n}}} $ ,且$ {c_{\rm{c}}} >{c_{\rm{n}}} >0 $ 。假设3 假设市场有两类消费者:以低碳消费为主的消费者和以传统消费为主的消费者。在衡量以低碳消费为主的消费者的效用时,忽略其传统消费的效用;在衡量以传统消费为主的消费者的效用时,忽略其低碳消费的效用。
假设4 低碳策略相应的低碳产品的市场需求取决于消费者剩余。
假设5 当政府进行补贴时,对企业的补贴额度不能超过其成本,对消费者的补贴额度不能超过低碳产品的售价。
基于前述假设,结合目前我国的政策现状,本文构建对消费者和企业同时补贴时低碳在企业和消费者中扩散的演化博弈模型,如表1所示。
表 1 演化博弈模型Table 1. The evolutionary game model主体及其策略选择 消费者行为 非低碳消费 低碳消费 企业 非低碳策略 $ {p_{\rm{n}}} - {c_{\rm{n}}} $, $ {U_{{\rm{nn}}}} $ $ - {c_{\rm{n}}} $,0 低碳策略 $ - {c_{\rm{c}}} + {w_1} $,0 $ {p_{\rm{c}}} - {c_{\rm{c}}} + {w_1} $, $ {U_{{\rm{cc}}}}' $ 表1中的参数含义如表2所示。部分参数的具体量化方式如下。1)
$ {w_1} = \varepsilon \left( {{c_{\rm{c}}} - {c_{\rm{n}}}} \right) $ ,其中,$ \varepsilon $ 为调整因子,且$ 0 <\varepsilon \leqslant 1 $ 。2) 借鉴文献[16],$ {U_{{\rm{nn}}}} = {\delta _{\rm{n}}}{\eta _{\rm{n}}} - {\tau _{\rm{n}}}{p_{\rm{n}}} $ ,其中,$ {\delta _{\rm{n}}} $ 表示非低碳消费者的环保偏好系数,且$ {\delta _{\rm{n}}} > 0 $ ;$ {\eta _{\rm{n}}} $ 表示非低碳产品的环保效用;$ {\tau _{\rm{n}}} $ 表示非低碳消费者的价格敏感系数,且$ {\tau _{\rm{n}}} >0 $ 。3) 借鉴文献[16],$ {{U_{{\rm{cc}}}'} } = {\delta _{\rm{c}}}{\eta _{\rm{c}}} - {\tau _{\rm{c}}}({p_{\rm{c}}} - {w_2}) $ ,其中,$ {\delta _{\rm{c}}} $ 表示低碳消费者的环保偏好系数,且$ {\delta _{\rm{c}}} >0 $ ;$ {\eta _{\rm{c}}} $ 表示低碳产品的环保效用,且$ {\eta _{\rm{c}}} >{\eta _{\rm{n}}} >0 $ ;$ {\tau _{\rm{c}}} $ 表示低碳消费者的价格敏感系数,且$ {\tau _{\rm{c}}} >0 $ ;$ {w_2} = {a_1} + {a_2} $ ,$ {a_1} $ 为价格补贴额度,$ {a_2} $ 为购置税补贴额度,且${a_2} = \dfrac{{{p_{\rm{c}}}}}{{1 + {\rm{v}}{{\rm{x}}_{\rm{t}}}}} \times 10 {\text{%}}$ ;$ {\rm{v}}{{\rm{x}}_{\rm{t}}} $ 是增值税。参数符号 参数意义描述 $ {p_{\rm{n}}} $ 采取非低碳策略对应的非低碳产品的价格 $ {c_{\rm{n}}} $ 采取非低碳策略的企业单位产品成本 $ {p_{\rm{c}}} $ 采取低碳策略对应的低碳产品的价格 $ {c_{\rm{c}}} $ 采取低碳策略的企业单位产品成本 $ {w_1} $ 政府对企业的补贴额度 $ {U_{{\rm{nn}}}} $ 非低碳偏好消费者消耗单位非低碳产品的消费者剩余 $ {U_{{\rm{cc}}}}' $ 低碳消费者消耗单位低碳产品的消费者剩余 设在
$ t $ 时刻,采取非低碳策略的企业比例为$ x $ ,则采取低碳策略的企业比例为$ 1 - x $ ;非低碳消费的消费者比例为$ y $ ,则采取低碳消费的消费者比例为$ 1 - y $ 。则根据上述假设和收益矩阵,可得复制动态方程组为$$\qquad \left\{ \begin{array}{l}{\rm{d}}x=x(1-x)[({p}_{{\rm{c}}}+{p}_{{\rm{n}}})y+(-{c}_{{\rm{n}}}-{p}_{{\rm{c}}}+{c}_{{\rm{c}}}-{w}_{1})]{\rm{d}}t\text{ };\;(1)\\ {\rm{d}}y=y(1-y)[({U}_{{\rm{nn}}}+{U}_{{\rm{cc}}}')x-{U}_{{\rm{cc}}}']{\rm{d}}t。\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\,(2)\end{array} \right. $$ 为了能够直接考虑企业采取低碳策略的收益和采取传统策略的收益之间,以及消费者采取低碳消费的收益和采取非低碳消费的收益之间的差异,本文将上述复制动态方程组调整为
$$ \qquad \left\{ \begin{array}{l}{\rm{d}}x=x[({p}_{{\rm{c}}}+{p}_{{\rm{n}}})y+(-{c}_{{\rm{n}}}-{p}_{{\rm{c}}}+{c}_{{\rm{c}}}-{w}_{1})]{\rm{d}}t\text{ };\;\;\;\;\;\;\;\;\;\;\;\;\,(3)\\ {\rm{d}}y=y[({U}_{{\rm{nn}}}+{U_{\rm{cc}}'})x-{U_{\rm{cc}}'}]{\rm{d}}t。\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\,\,\,\,(4)\end{array} \right. $$ 1.2 随机演化博弈模型的建立
上述确定性演化博弈模型存在如下问题。1) 由企业群体和消费者群体构成的系统为复杂系统,其演化的动力学机制具有不确定性,受到一些不确定性因素(如企业的风险偏好、预期收益水平)的影响。同时,企业所处的外部环境(如政治、经济、文化环境)也会对其决策有影响,进而影响低碳扩散过程的稳定性。2) 消费者的策略选择会受到一些不确定因素(如消费者收入水平的变化、周围人的消费意识)的影响。因此,低碳扩散的演化过程表现为不确定性。为此,基于上述确定性演化博弈模型,建立的随机演化博弈模型为
$$ \begin{split} &\qquad {\rm{d}}x(t) = x(t)({\pi _{{\rm{AN}}}} - {\pi _{{\rm{AC}}}}) = x(t)[({p_{\rm{c}}} + {p_{\rm{n}}})y(t) + ( - {c_{\rm{n}}} - {p_{\rm{c}}} + \\ & {c_{\rm{c}}} - {w_1})]{\rm{d}}t + \sigma x(t){\rm{d}}w(t); \end{split} $$ (5) $$\begin{split} &\qquad {\rm{d}}y(t) = y(t)({\pi _{{\rm{SN}}}} - {\pi _{{\rm{SC}}}}) = y(t)[({U_{{\rm{nn}}}} + {{U_{{\rm{cc}}}'} })x(t) - {{U_{{\rm{cc}}}'} }]{\rm{d}}t +\\ &\sigma y(t){\rm{d}}w(t)。 \end{split} $$ (6) 其中,
$ w(t) $ 服从标准的一维布朗运动;$ {\rm{d}}w(t) $ 为高斯白噪声;当$ t >0 $ ,$ h >0 $ 时,其增量$ \Delta w(t) = w(t + h) - w(t) $ 服从正态分布$ N(0,\;\sqrt h ) $ ;$ \sigma $ 表示噪声强度,且$ \sigma >0 $ 。2. 稳定性判据及情形分析
2.1 稳定性判据
假设初始时刻
$ t = 0 $ ,$ x(t) = x(0) = 0 $ ,$ y(t) = y(0) = 0 $ 是随机微分方程组的解,本文也将初始状态记作$ {x_0} $ 和$ {y_0} $ ,此时,企业全部采用低碳策略,消费者全部是低碳消费者。但是,系统总会受到内外部环境变化的影响,进而影响其稳定性。因此,有必要考虑随机因素作用下系统的稳定状态。根据文献[17],有如下引理。引理 给定一个随机微分方程
$$ \begin{array}{l}\qquad {\rm{d}}x(t) = f(t,\;x(t)){\rm{d}}t + g(t,\;x(t)){\rm{d}}w(t),\;x({t_0}) \equiv {x_0} 。\end{array} $$ (7) 设存在
$ V(t,\;x) \in {H^{1,\;2}}({{\text{R}}_ + } \times {{\text{R}}^d}) $ 与正常数$ {h_1},\;{h_2} $ ,使得$ {h_1}{\left| x \right|^p} \leqslant V(t,\;x) \leqslant {h_2}{\left| x \right|^p} $ ,则1) 若存在正常数
$ \gamma $ ,使得$ {\rm{LV}}(t,\;x) \leqslant - \gamma V(t,\;x) $ ,则方程(7)的零解P阶矩指数稳定,且成立$ E{\left| {x(t,\;{x_0})} \right|^p} \leqslant ({h_2}/{h_1}){\left| {{x_0}} \right|^p}{{\rm{e}}^{ - \gamma t}} $ ;2) 若存在正常数
$ \gamma $ ,使得$ {\rm{LV}}(t,\;x) \geqslant \gamma V(t,\;x) $ ,则方程(7)的零解P阶矩指数不稳定,且成立$ E{\left| {x(t,\;{x_0})} \right|^p} \geqslant ({h_2}/{h_1}){\left| {{x_0}} \right|^p}{{\rm{e}}^{ - \gamma t}} $ 。根据上述引理,得出如下结论,用以判断企业和消费者行为的演化稳定性。
命题1 针对方程(5),取
$ V(t,\;x(t)) = x(t) $ ,$ x(t) \in [0,\;1] $ ,${h_1} = {h_2} = 1$ ,$p = 1$ ,$\gamma = 1$ ,则${\rm{LV}}(t,\;x(t)) = f(t,\;x(t))$ 。于是有:1) 当$ y(t) \leqslant \dfrac{{{c_{\rm{n}}} + {p_{\rm{c}}} - {c_{\rm{c}}} + {w_1} - 1}}{{{p_{\rm{n}}} + {p_{\rm{c}}}}} $ ,且$ {c_{\rm{n}}} + {p_{\rm{c}}} - {c_{\rm{c}}} + {w_1} \geqslant 1 $ 时,方程(5)的零解矩指数稳定;2) 当$ y(t) \geqslant \dfrac{{{c_{\rm{n}}} + {p_{\rm{c}}} - {c_{\rm{c}}} + {w_1} + 1}}{{{p_{\rm{n}}} + {p_{\rm{c}}}}} $ ,且$ {p_{\rm{n}}} - {c_{\rm{n}}} + {c_{\rm{c}}} - {w_1} \geqslant 1 $ 时,方程(5)的零解矩指数不稳定。证明 对于方程(5),取
$ {h_1} = {h_2} = 1 $ ,$ p = 1 $ ,$ \gamma = 1 $ ,$ V(t,\;x(t)) = x(t) $ 时,$ {\rm{LV}}(t,\;x(t)) = f(t,\;x(t)) = x(t)[({p_{\rm{c}}} + {p_{\rm{n}}}) \times y(t) + ( - {c_{\rm{n}}} - {p_{\rm{c}}} + {c_{\rm{c}}} - {w_1})] $ 。1) 当方程(5)零解矩指数稳定时,需满足
$ x(t)[({p_{\rm{c}}} + {p_{\rm{n}}})y(t) + ( - {c_{\rm{n}}} - {p_{\rm{c}}} + {c_{\rm{c}}} - {w_1}] \leqslant - x(t) $ 。由于$ x(t) \in [0,\;1] $ ,故$({p_{\rm{c}}} + {p_{\rm{n}}})y(t) + ( - {c_{\rm{n}}} - {p_{\rm{c}}} + {c_{\rm{c}}} - {w_1}) + 1 \leqslant 0$ ,得$y(t) \leqslant \dfrac{{{c_{\rm{n}}} + {p_{\rm{c}}} - {c_{\rm{c}}} + {w_1} - 1}}{{{p_{\rm{n}}} + {p_{\rm{c}}}}}$ ,且满足$ \dfrac{{{c_{\rm{n}}} + {p_{\rm{c}}} - {c_{\rm{c}}} + {w_1} - 1}}{{{p_{\rm{n}}} + {p_{\rm{c}}}}} \geqslant 0 $ ,故可得方程(5)的零解矩指数稳定条件为$ y(t) \leqslant \dfrac{{{c_{\rm{n}}} + {p_{\rm{c}}} - {c_{\rm{c}}} + {w_1} - 1}}{{{p_{\rm{n}}} + {p_{\rm{c}}}}} $ ,且$ {c_{\rm{n}}} + {p_{\rm{c}}} - {c_{\rm{c}}} + {w_1} \geqslant 1 $ 。2) 当方程(5)零解矩指数不稳定时,需满足
$ x(t)[({p_{\rm{c}}} + {p_{\rm{n}}})y(t) + ( - {c_{\rm{n}}} - {p_{\rm{c}}} + {c_{\rm{c}}} - {w_1}] \geqslant x(t) $ ,故$({p_{\rm{c}}} + {p_{\rm{n}}}) \times y(t) + ( - {c_{\rm{n}}} - {p_{\rm{c}}} + {c_{\rm{c}}} - {w_1}) \geqslant 1$ ,计算可得$y(t) \geqslant \ \dfrac{{{c_{\rm{n}}} + {p_{\rm{c}}} - {c_{\rm{c}}} + {w_1} + 1}}{{{p_{\rm{n}}} + {p_{\rm{c}}}}}$ ,且满足$ \dfrac{{{c_{\rm{n}}} + {p_{\rm{c}}} - {c_{\rm{c}}} + {w_1} - 1}}{{{p_{\rm{n}}} + {p_{\rm{c}}}}} \leqslant 1 $ ,故可得方程(5)的零解矩指数不稳定条件为$ y(t) \geqslant \dfrac{{{c_{\rm{n}}} + {p_{\rm{c}}} - {c_{\rm{c}}} + {w_1} + 1}}{{{p_{\rm{n}}} + {p_{\rm{c}}}}} $ ,且$ {p_{\rm{n}}} - {c_{\rm{n}}} + {c_{\rm{c}}} - {w_1} \geqslant 1 $ 。命题1表明,当采取非低碳消费的消费者比例满足条件1) 时,企业群体最终将选择低碳策略;当该比例满足条件2) 时,企业群体最终更倾向于采取非低碳策略。
命题2 针对方程(6),取
$ V(t,\;y(t)) = y(t) $ ,$ y(t) \in [0,\;1] $ ,${h_1} = {h_2} = 1$ ,$p = 1$ ,$\gamma = 1$ ,则${\rm{LV}}(t,\;y(t)) = f(t,\;y(t))$ 。于是有:1) 当$ x(t) \leqslant \dfrac{{{{U_{{\rm{cc}}}'} } - 1}}{{{{U_{{\rm{cc}}}'} } + {U_{{\rm{nn}}}}}} $ 且$ {{U_{{\rm{cc}}}'} } \geqslant 1 $ 时,方程(6)的零解矩指数稳定;2) 当$ x(t) \geqslant \dfrac{{{{U_{{\rm{cc}}}'} } + 1}}{{{{U_{{\rm{cc}}}'} } + {U_{{\rm{nn}}}}}} $ 且$ {U_{{\rm{nn}}}} \geqslant 1 $ 时,方程(6)的零解矩指数不稳定。命题2的证明过程同命题1。
命题2表明,当采取非低碳策略的企业比例满足条件1) 时,消费者群体最终会选择低碳消费;当该比例满足条件2) 时,消费者群体更倾向于选择非低碳消费。
同时,由于
$\dfrac{{{{U_{{\rm{cc}}}'} } - 1}}{{{{U_{{\rm{cc}}}'} } + {U_{{\rm{nn}}}}}} < \dfrac{{{{U_{{\rm{cc}}}'} } + 1}}{{{{U_{{\rm{cc}}}'} } + {U_{{\rm{nn}}}}}}$ ,$\dfrac{{{c_{\rm{n}}} + {p_{\rm{c}}} - {c_{\rm{c}}} + {w_1} - 1}}{{{p_{\rm{n}}} + {p_{\rm{c}}}}} < \dfrac{{{c_{\rm{n}}} + {p_{\rm{c}}} - {c_{\rm{c}}} + {w_1} + 1}}{{{p_{\rm{n}}} + {p_{\rm{c}}}}}$ ,因此,两个稳定性状态的边界并不重合,存在中间区域没有被覆盖,且该区域为$ \dfrac{{{{U_{{\rm{cc}}}'} } - 1}}{{{{U_{{\rm{cc}}}'} } + {U_{{\rm{nn}}}}}} < x(t) < \dfrac{{{{U_{{\rm{cc}}}'} } + 1}}{{{{U_{{\rm{cc}}}'} } + {U_{{\rm{nn}}}}}} $ ,$ \dfrac{{{c_{\rm{n}}} + {p_{\rm{c}}} - {c_{\rm{c}}} + {w_1} - 1}}{{{p_{\rm{n}}} + {p_{\rm{c}}}}} < y(t) < \dfrac{{{c_{\rm{n}}} + {p_{\rm{c}}} - {c_{\rm{c}}} + {w_1} + 1}}{{{p_{\rm{n}}} + {p_{\rm{c}}}}} $ 。在本文中,称该区域为混沌区域。2.2 稳定性情形分析
根据上述内容,低碳扩散过程可以划分为3种稳定情形。
情形1
$ 0 \leqslant x \leqslant \dfrac{{{{U_{{\rm{cc}}}'} } - 1}}{{{{U_{{\rm{cc}}}'} } + {U_{{\rm{nn}}}}}} $ ,$ 0 \leqslant y \leqslant \dfrac{{{c_{\rm{n}}} + {p_{\rm{c}}} - {c_{\rm{c}}} + {w_1} - 1}}{{{p_{\rm{n}}} + {p_{\rm{c}}}}} $ ,其中,$ {{U_{{\rm{cc}}}'} } \geqslant 1 $ ,$ {c_{\rm{n}}} + {p_{\rm{c}}} - {c_{\rm{c}}} + {w_1} \geqslant {\text{1}} $ 。当采取非低碳策略的企业和采取非低碳消费的消费者比例满足上述条件时,系统存在唯一演化稳定策略ESS(0, 0),即企业群体和消费者群体最终分别会采取低碳策略和低碳消费,这是一种有效率的稳定状态。
情形2
$ \dfrac{{{{U_{{\rm{cc}}}'} } + 1}}{{{{U_{{\rm{cc}}}'} } + {U_{{\rm{nn}}}}}} \leqslant x \leqslant 1 $ ,$ \dfrac{{{c_{\rm{n}}} + {p_{\rm{c}}} - {c_{\rm{c}}} + {w_1} + 1}}{{{p_{\rm{n}}} + {p_{\rm{c}}}}} \leqslant y \leqslant 1 $ ,其中,$ {p_{\rm{n}}} - {c_{\rm{n}}} + {c_{\rm{c}}} - {w_1} \geqslant 1 $ ,$ {U_{{\rm{nn}}}} \geqslant 1 $ 。当采取非低碳策略的企业和采取非低碳消费的消费者比例满足上述条件时,系统存在唯一演化稳定策略(1, 1),即企业群体和消费者群体最终会分别采取非低碳策略和非低碳消费,这是一种无效率的稳定状态。
值得一提的是,这种状态是在一定的噪声强度前提下存在的,当噪声强度增大到一定程度时,仍然有很大概率稳定于(0, 0)点,即很有可能向有效率状态发展,这也是在该条件下零解矩指数不稳定的体现。
情形3
$ \dfrac{{{{U_{{\rm{cc}}}'} } - 1}}{{{{U_{{\rm{cc}}}'} } + {U_{{\rm{nn}}}}}} <x < \dfrac{{{{U_{{\rm{cc}}}'} } + 1}}{{{{U_{{\rm{cc}}}'} } + {U_{{\rm{nn}}}}}} $ ,$\dfrac{{{c_{\rm{n}}} + {p_{\rm{c}}} - {c_{\rm{c}}} + {w_1} - 1}}{{{p_{\rm{n}}} + {p_{\rm{c}}}}} < y < \dfrac{{{c_{\rm{n}}} + {p_{\rm{c}}} - {c_{\rm{c}}} + {w_1} + 1}}{{{p_{\rm{n}}} + {p_{\rm{c}}}}}$ 。其中,${p_{\rm{n}}} - {c_{\rm{n}}} + {c_{\rm{c}}} - {w_1} \geqslant 1$ ,$ {U_{{\rm{nn}}}} \geqslant 1 $ 。当采取非低碳策略的企业和采取非低碳消费的消费者比例满足上述条件时,系统既有可能向稳定状态(0, 0)演化,也有可能向稳定状态(1, 1)演化,即企业最终有可能选择低碳策略,也有可能选择非低碳策略,而消费者最终有可能选择低碳消费,也有可能选择非低碳消费,这是一种混沌状态。
3. 仿真分析
下面以新能源汽车比亚迪E6和非新能源汽车比亚迪M6为例,通过仿真分析来说明上述研究内容的应用。根据所搜集的资料并结合文献[18],获取以下相关数据:
$ {p_{\rm{c}}} = 33.98 $ ,$ {c_{\rm{c}}} = 25 $ ,$ {p_{\rm{n}}} = 12.89 $ ,$ {c_{\rm{n}}} = 5.54 $ ,$ {a_1} = 5.5 $ ,$ {{\rm{vx}}_{\rm{t}}} = 17{\text{% }} $ ,$ {a_2} = 2.9 $ ,$ {w_1} = 19.46 $ ,$ {w_2} = 8.4 $ ,$ {\eta _{\rm{c}}} = 50 $ ,$ {\eta _{\rm{n}}} = 40 $ ,${\tau _{\rm{c}}} = 1$ ,${\tau _{\rm{n}}} = 1$ ,${\delta _{\rm{c}}} = 1.2$ ,${\delta _{\rm{n}}} = 1$ ,$ {U_{{\rm{nn}}}} = 27.11 $ ,$ {{U_{{\rm{cc}}}'} } = 37.02 $ 。将上述数值代入式(5)和式(6),得
$$\qquad {\rm{d}}x = x(46.87y - 33.98){\rm{d}}t + \sigma x{\rm{d}}w(t){\text{ }};$$ (8) $$\qquad {\rm{d}}y = y(64.13x - 37.02){\rm{d}}t + \sigma y{\rm{d}}w(t){\text{ }}。$$ (9) 同时,低碳扩散的3种稳定情形如下。
情形1
$ 0 \leqslant x \leqslant 56.17\% $ ,$ 0 \leqslant y \leqslant 70.17\% $ 。情形2
$ 59.29\% \leqslant x \leqslant 1 $ ,$ 74.63\% \leqslant y \leqslant 1 $ 。情形3
$ 56.17\% < x < 59.29\% $ ,$ 70.17\% < y < 74.63\% $ 。本文将噪声强度设为4种:
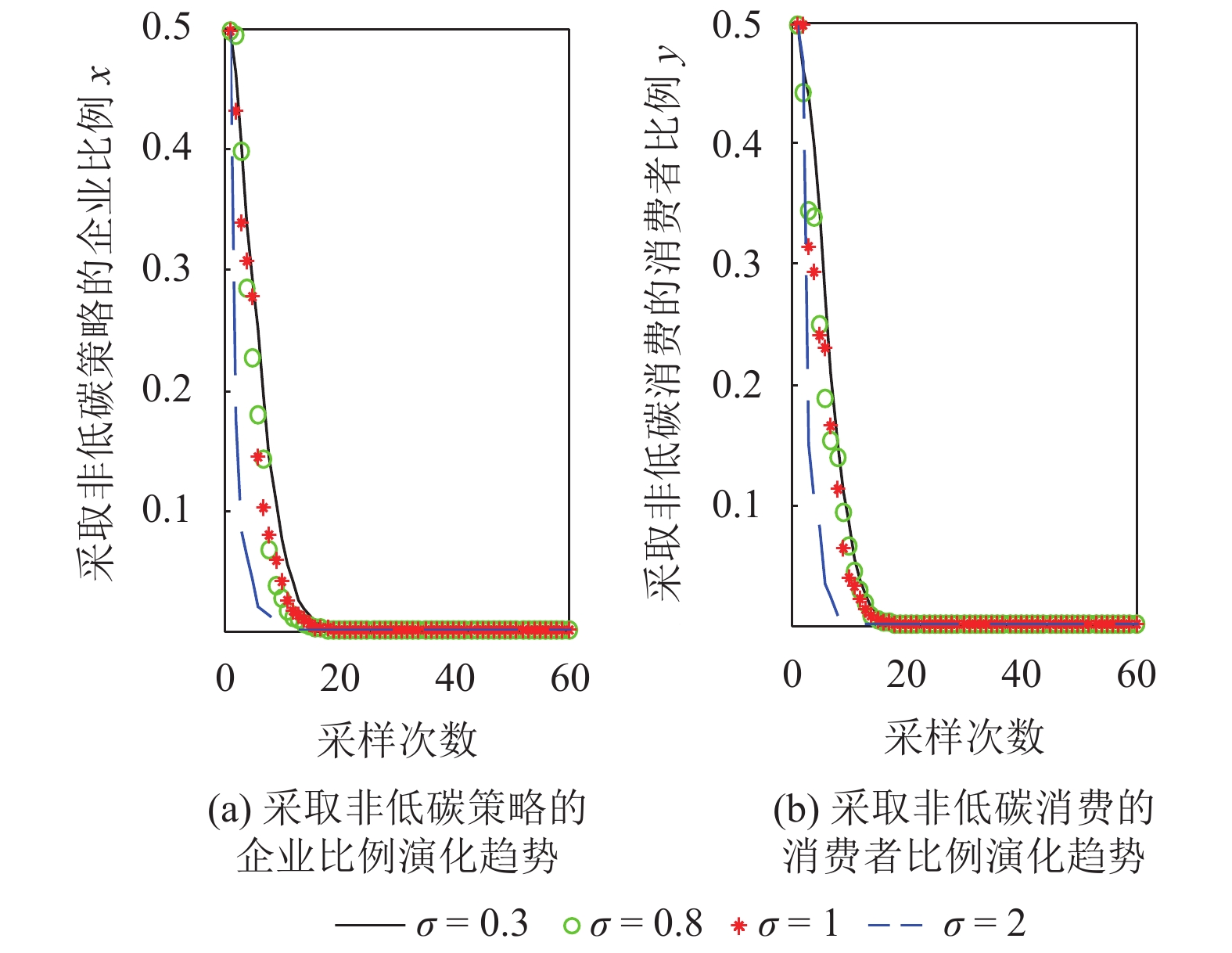
$ \sigma = 0.3 $ ,$ \sigma = 0.8 $ ,$ \sigma = 1 $ ,$ \sigma = 2 $ 。下面分别对比亚迪 E6扩散的3种稳定情形进行仿真,同时在每种情形中考虑不同噪声强度对比亚迪 E6扩散稳定性的影响,由于噪声的存在,每种情形的仿真结果都是以一定概率出现的,本文只考虑最大概率出现的仿真结果,如图1~3所示。1) 当
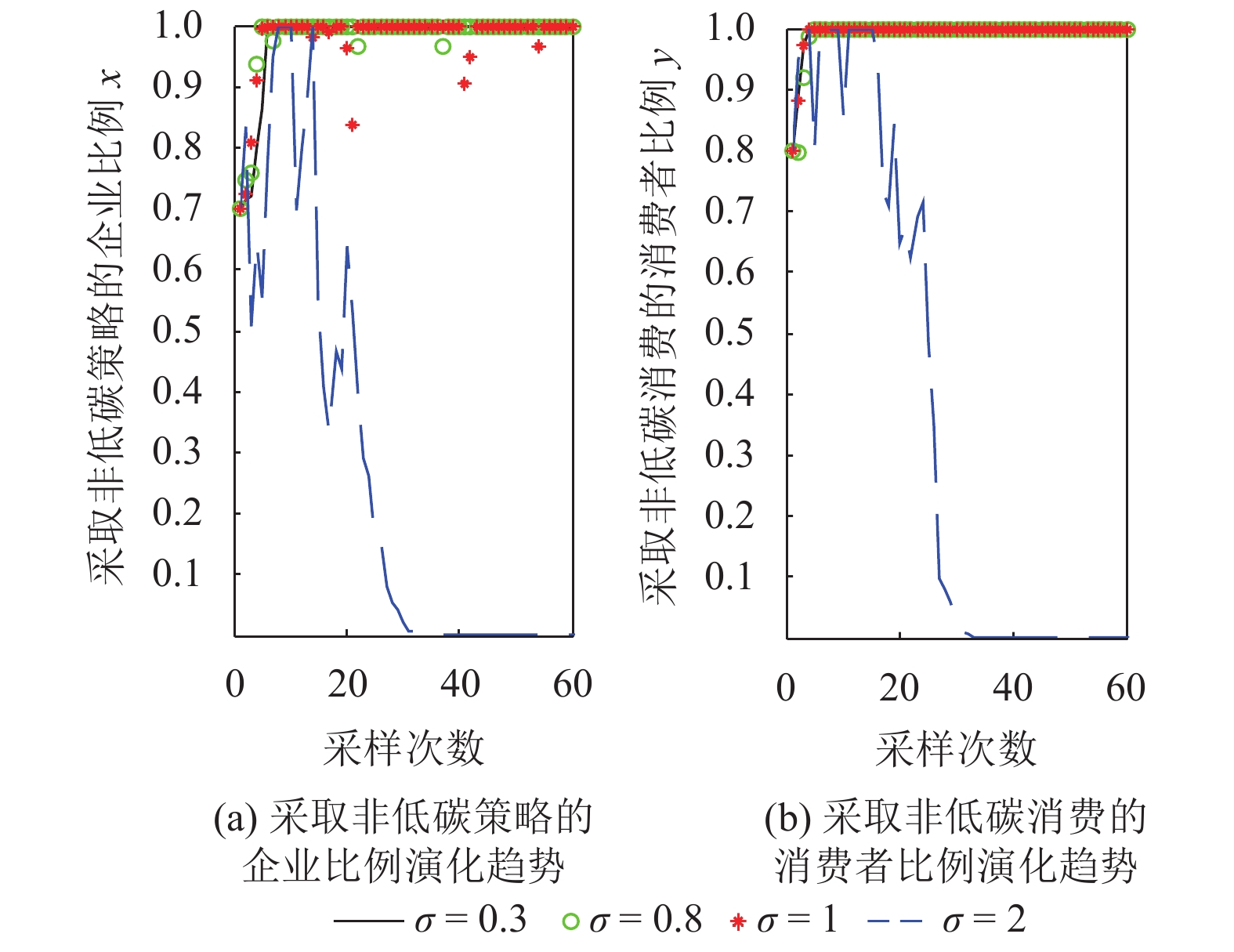
$ 0 \leqslant x \leqslant 56.17\% $ ,$ 0 \leqslant y \leqslant 70.17\% $ ,取$ {x_0} = 0.5 $ ,$ {y_0} = 0.5 $ 。由图1可知,当
$ {x_0} = 0.5 $ ,$ {y_0} = 0.5 $ 时,即生产比亚迪 M6的企业比例和购买比亚迪 M6的消费者比例分别为0.5和0.5,此时生产比亚迪 E6的企业比例和购买比亚迪E6的消费者比例分别为0.5和0.5,系统最终可以稳定在(0,0)这个状态,也就是说,在不同的噪声强度下,比亚迪 E6在企业和消费者中可以实现有效扩散,且演化到稳定状态的次数相同。在次数约为18时,企业全部生产比亚迪 E6,消费者全部消费比亚迪 E6。情形1得证。2) 当
$ 59.29\% \leqslant x \leqslant 1 $ ,$ 74.63\% \leqslant y \leqslant 1 $ ,取$ x_0^{} = 0.7 $ ,$ {y_0} = 0.8 $ 。由图2可知,当
$ x_0^{} = 0.7 $ ,$ {y_0} = 0.8 $ 时,即生产比亚迪 M6的企业比例和购买比亚迪 M6的消费者比例分别为0.7和0.8。此时,生产比亚迪E6的企业比例和购买比亚迪E6的消费者比例分别为0.3和0.2。在不同的噪声强度下,最终实现的稳定状态也略有不同,且演化到稳定状态的次数也不相同。当噪声强度为0.3、0.8和1时,企业全部生产比亚迪M6,消费者全部消费比亚迪 M6,此时低碳最终没有扩散至有效状态。而当噪声强度为2时,演化结果则相反。企业全部生产比亚迪E6,消费者全部消费比亚迪 E6。可见,当噪声强度增大到一定程度时,可以影响到比亚迪 E6的最终扩散结果,同时也说明不确定性程度的增大不一定会带来不利的结果。情形 2得证。同时,根据情形1和情形2的仿真结果可知,当比亚迪 E6最终扩散至有效状态时,在同一种噪声强度下,总是消费者先实现有效稳定(
$ y = 0 $ ),然后企业才实现有效稳定($ x = 0 $ ),即比亚迪 E6在企业中的有效扩散具有滞后性。同时,比亚迪 E6在企业中扩散的波动性总是高于比亚迪 E6在消费者中扩散的波动性,即消费者对企业实施低碳策略的影响要远大于企业对消费者实施低碳消费的影响。3) 当
$ 56.17\% < x < 59.29\% $ ,$ 70.17\% < y < 74.63\% $ 时,取$ {x_0} = 0.58 $ ,$ {y_0} = 0.73 $ 。由图3可知,当
$ 56.17\% < x < 59.29\% $ ,$ 70.17\% < y < 74.63\% $ 时,市场是一种混沌状态,有可能最终稳定在均衡点(0,0),也有可能最终稳定在均衡点(1,1),且噪声的影响也没有明显的规律。因此,情形 3得证。通过上述仿真结果可知,在噪声环境下,不同的初始值状态对低碳扩散的稳定性有很大的影响。在实际的管理过程中,可以采取以下策略引导企业和消费者的行为,进而确保低碳扩散的有效稳定。
1) 提高企业和消费者对低碳的认知水平,采用宣传、培训等措施,利用网络和自媒体等手段,内在引导企业和消费者分别采取低碳策略和低碳消费;同时,实施多元化激励措施,如补贴、碳税、保险等,外在激励企业和消费者的低碳行为。
2) 辩证看待环境的不确定性。不确定性造成模糊和混沌市场环境的同时,也蕴藏着机遇,此刻更应增强企业对低碳生产的信心,通过典型低碳实施成功案例分享进行反馈和交流,间接影响企业的心理,促使其低碳行为模仿,从而提高企业实施低碳生产的整体水平。
3) 通过刺激市场的低碳产品需求来拉动市场的低碳产品供应。同时,提高企业对低碳技术创新的重视程度,增加人财物等方面的低碳投入,加大风险控制力度,积极推进低碳在企业和消费者中的扩散。
4) 为企业和消费者建立良好的低碳预期,尤其在不确定性程度比较大的市场环境下,政府应当及时地完善低碳政策制度,确保低碳政策的一致性和连续性,加强企业和消费者实施低碳行为的信心。同时,进行低碳文化建设,从文化层面上引导企业和消费者的低碳行为。
4. 结论
本文以异质性主体中的低碳扩散为研究对象,运用随机演化博弈方法研究其稳定性问题,以新能源汽车比亚迪E6和传统汽车M6为例验证了有效稳定、无效稳定和混沌3种稳定情形。研究表明,低碳在企业中的扩散具有滞后性,且消费者对企业实施低碳策略的影响要远大于企业对消费者实施低碳消费的影响,因此,通过需求方拉动低碳市场比通过供给方推动市场更能较快地实现低碳的有效扩散。同时,当采取低碳策略的企业比例和采取低碳消费的消费者比例都较低时,在不同的噪声强度下,无法实现低碳策略和低碳消费的成功扩散,随着采取低碳策略的企业比例和采取低碳消费的消费者比例的增加,低碳扩散最终可以实现有效稳定状态。此外,外部环境的不确定程度的增加并不一定是危机,有时是一种机遇。研究有助于企业理性地把握低碳扩散的规律,适时采取低碳策略,进而规避风险。同时也有利于政府理性地把握市场主体的行为,充分发挥政府的调控作用,提高市场效率进而促进低碳扩散,实现有效稳定。
-
表 1 演化博弈模型
Table 1 The evolutionary game model
主体及其策略选择 消费者行为 非低碳消费 低碳消费 企业 非低碳策略 pn−cn, Unn −cn,0 低碳策略 −cc+w1,0 pc−cc+w1, Ucc′ -
[1] SHI Y Y, HAN B T, ZENG Y C. Simulating policy interventions in the interfirm diffusion of low-carbon technologies: an agent-based evolutionary game model[J]. Journal of Cleaner Production, 2020, 250: 1-10.
[2] LI W J, RUIZ-MENJIVAR J, ZHANG L, et al. Climate change perceptions and the adoption of low-carbon agricultural technologies: evidence from rice production systems in the Yangtze River Basin[J]. Science of the Total Environment, 2021, 759: 1-12.
[3] LAI X D, LIU J X, SHI Q, et al. Driving forces for low carbon technology innovation diffusion in the building industry: a critical review[J]. Renewable and Sustainable Energy Reviews, 2017, 74: 299-315. DOI: 10.1016/j.rser.2017.02.044
[4] BI K X, HUANG P, WANG X X. Innovation performance and influencing factors of low-carbon technological innovation under the global value chain: a case of Chinese manufacturing industry[J]. Technological Forecasting & Social Change, 2016, 111: 275-284.
[5] 徐莹莹, 綦良群. 基于复杂网络演化博弈的企业集群低碳技术创新扩散研究[J]. 中国人口. 资源与环境, 2016, 26(8): 16-24. XU Yingying, QI Liangqun. Research on low carbon technological innovation diffusion in enterprises clusters based on evolutionary game theory on complex networks[J]. China Population Resources and Environment, 2016, 26(8): 16-24.
[6] KUMAR R, AGARWALA A. Renewable energy technology diffusion model for techno-economics feasibility[J]. Renewable and Sustainable Energy Reviews, 2016, 54: 1515-1524. DOI: 10.1016/j.rser.2015.10.109
[7] ZHANG L P, XUE L, ZHOU Y. How do low-carbon policies promote green diffusion among alliance-based firms in China? An evolutionary-game model of complex networks[J]. Journal of Cleaner Production, 2019, 210: 518-529. DOI: 10.1016/j.jclepro.2018.11.028
[8] WAN B Y, TIAN L X, ZHU N P, et al. A new endogenous growth model for green low-carbon behavior and its comprehensive effects[J]. Applied Energy, 2018, 230: 1332-1346. DOI: 10.1016/j.apenergy.2018.09.076
[9] 袭希, 侯勇, 赵健宇. 低碳技术在市场中扩散的逾渗模型: 基于新能源乘用汽车产业的仿真分析[J]. 系统工程, 2020, 38(5): 46-54. XI Xi, HOU Yong, ZHAO Jianyu. A percolation model on diffusion of low-carbon technology in the market−simulation analysis on new energy passenger vehicle industry[J]. Systems Engineering, 2020, 38(5): 46-54.
[10] 付秋芳, 忻莉燕, 马士华. 惩罚机制下供应链企业碳减排投入的演化博弈[J]. 管理科学学报, 2016, 19(4): 56-70. DOI: 10.3969/j.issn.1007-9807.2016.04.005 FU Qiufang, XIN Liyan, MA Shihua. Evolutionary game of carbon-emission-reduction investment in supply chains under a contract with punishment mechanism[J]. Journal of Management Science in China, 2016, 19(4): 56-70. DOI: 10.3969/j.issn.1007-9807.2016.04.005
[11] 吕希琛, 徐莹莹, 徐晓薇. 环境规制下制造业企业低碳技术扩散的动力机制——基于小世界网络的仿真研究[J]. 中国科技论坛, 2019(7): 145-156. LYU Xichen, XU Yingying, XU Xiaowei. Motivation mechanism of low-carbon technology diffusion in manufacturing enterprises under environmental regulation−simulation research based on small world network[J]. Forum on Science and Technology in China, 2019(7): 145-156.
[12] LYAPUNOV A M. The general problem of the stability of motion[J]. International Journal of Control, 1992, 55: 531-534. DOI: 10.1080/00207179208934253
[13] PIMM S L. The balance of nature. Ecological issues in the conservation of species and communities[M]. Chicago: University of Chicago Press, 1991.
[14] 孙华丽, 王循庆, 薛耀锋. 基于不同情景的群体性突发事件随机演化博弈模型[J]. 运筹与管理, 2016, 25(4): 23-30. SUN Huali, WANG Xunqing, XUE Yaofeng. Stochastic evolutionary game model for unexpected incidents involving mass participation based on different scenarios[J]. Operations Research and Management Science, 2016, 25(4): 23-30.
[15] 李莹, 陶元磊. 散户参与家庭农场的稳定性分析——基于随机演化博弈视角[J]. 技术经济与管理研究, 2015(4): 20-24. DOI: 10.3969/j.issn.1004-292X.2015.04.004 LI Ying, TAO Yuanlei. Analysis of the stability of small farmers participating in family farm−based on the random evolution game theory[J]. Journal of Technical Economics & Management, 2015(4): 20-24. DOI: 10.3969/j.issn.1004-292X.2015.04.004
[16] 徐朗, 汪传旭, 杨清荃. 低碳背景下政府财税行为对制造商决策行为[J]. 工业工程, 2016, 19(3): 30-36. DOI: 10.3969/j.issn.1007-7375.2016.03.006 XU Lang, WANG Chuanxu, YANG Qingquan. The impact of government fiscal behavior on the manufacturer's decision under the background of low-carbon[J]. Industry Engineering Journal, 2016, 19(3): 30-36. DOI: 10.3969/j.issn.1007-7375.2016.03.006
[17] 胡适耕, 黄乘明, 吴付科. 随机微分方程[M]. 北京: 科学出版社, 2008. [18] FAN R G, DONG L L. The dynamic analysis and simulation of government subsidy strategies in low-carbon diffusion considering the behavior of heterogeneous agents[J]. Energy Policy, 2018, 117: 252-262. DOI: 10.1016/j.enpol.2017.12.003
-
期刊类型引用(0)
其他类型引用(3)



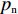
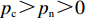
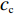
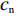
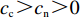
 下载:
下载: