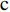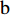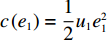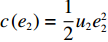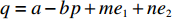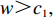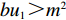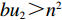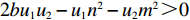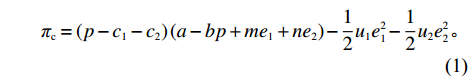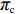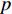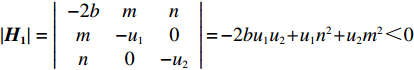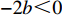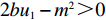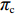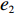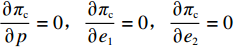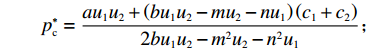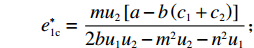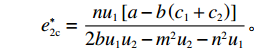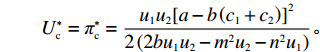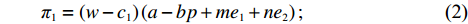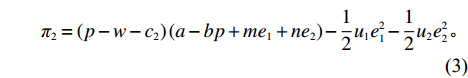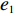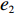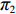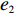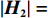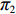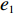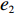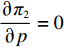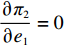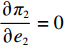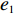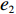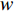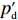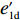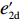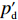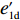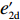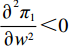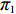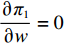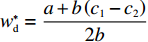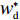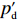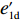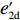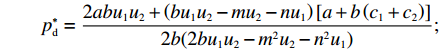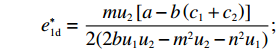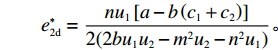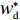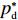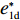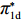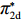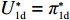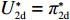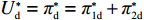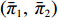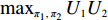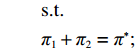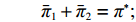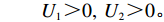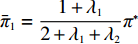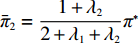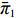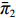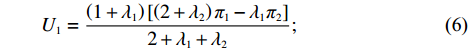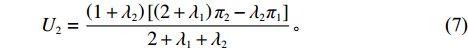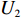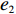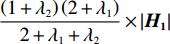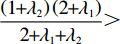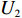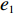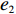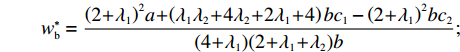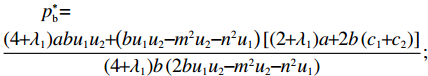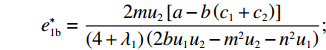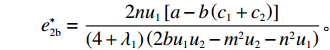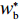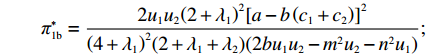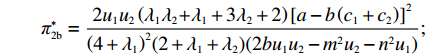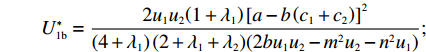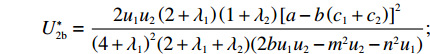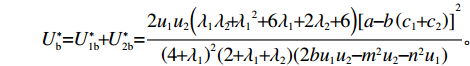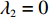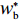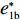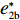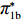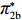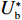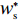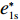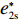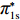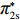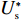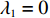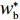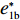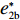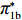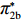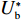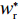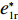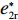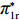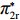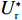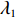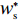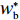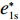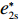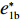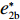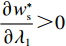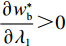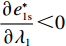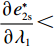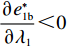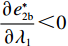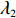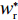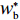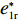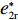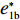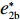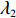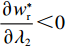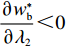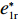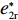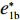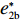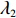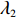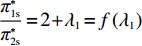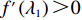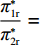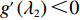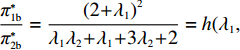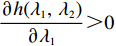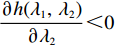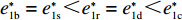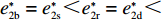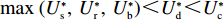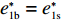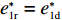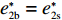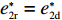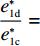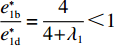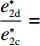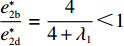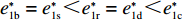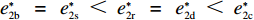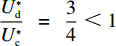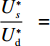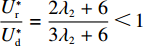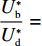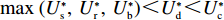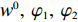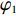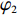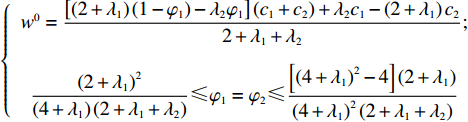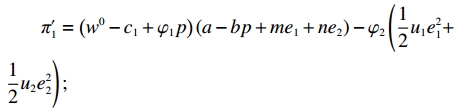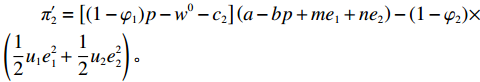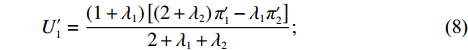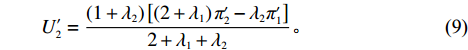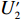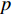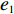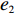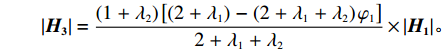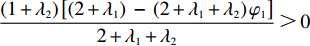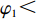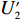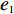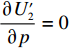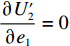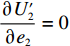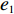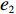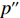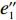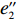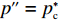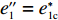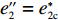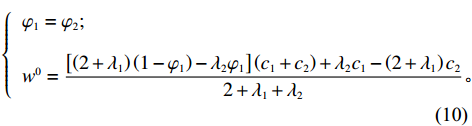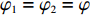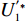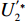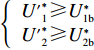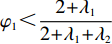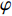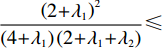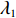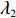A Research on Decision-makings and Coordination of Fresh-product Supply Chain in “Pre-Position Warehouse Mode” under Fairness Concern
-
摘要:
针对由生鲜产品供应商和“前置仓模式”下的生鲜电商组成的二级供应链保鲜努力水平和“最后一公里服务”努力水平偏低的问题，从公平关切视角探究其原因。运用博弈论方法，通过建立Nash讨价还价模型，分析与比较不同公平关切情形下供应链主体的最优决策以及与之对应的收益和效用。结果表明，供应商的公平关切会降低生鲜电商保鲜努力水平和“最后一公里服务”努力水平，而且供应链成员的公平关切总是伴随着各自渠道收益比的提升和供应链总效用的损失。最后，通过设计“收益共享+成本分担”混合契约，提高电商保鲜努力水平和“最后一公里服务”努力水平，使供应链总效用达到最优。数值分析验证了相关结论。
-
关键词:
- 前置仓模式 /
- 公平关切 /
- 保鲜努力 /
- “最后一公里服务”努力 /
- 混合契约
Abstract:In view of the low level of fresh-keeping efforts and “last kilometer service” efforts of the two-echelon supply chain consisting of a fresh product supplier and an online fresh product retailer in "pre-position warehouse mode", the reasons were explored from the perspective of fairness concern. By using the game theory method and establishing the Nash bargaining model, optimal decision-makings as well as the earnings and utility of the supply chain were analyzed and compared under different fairness concern conditions. The result indicates that the supplier's fairness concern can lower the online retailer's fresh-keeping efforts and the “last kilometer service” efforts. Moreover, fairness concerns of supply chain members are generally accompanied by an increase of their earnings ratio and the loss of the total supply chain utility. Finally, the efforts level of fresh-keeping and “last kilometer service” can both be improved, and the total utility of the supply chain can be optimized by the hybrid contract which emphasizes earnings and cost sharing. The result was verified by a numerical analysis.
-
随着经济的发展，消费者越来越注重商品质量和服务体验。在此背景下，每日优鲜、朴朴超市和叮咚买菜作为纯线上生鲜零售商−前置仓模式(以下称“前置仓模式”)的电商代表，得到了人们的广泛关注。在“前置仓模式”下，影响消费者和供应链成员的决策因素与普通生鲜供应链(以下称普通供应链)存在很大差异。有关普通供应链的研究大多假设消费者购买生鲜商品时主要考虑商品价格和新鲜度[1-3]，而供应链成员主要考虑商品如何定价和为维持商品新鲜度要付出多高水平的保鲜努力[4]。多数情况下，由于生鲜商品的保鲜需要付出额外成本，却不能为保鲜责任方带来超额收益，因此他们往往只付出低水平的保鲜努力，导致商品新鲜度较差，消费者效用低，而供应链成员也并未取得最大效益。基于此，学者们开始考虑用成本分摊契约[5]、收益共享契约[6]或两者兼施的混合契约[7- 8]来激励保鲜责任方提高保鲜努力水平或提高供应链总效用。但是在“前置仓模式”下，除了价格和新鲜度外，生鲜的配送及时性、配送人员的服务态度、包装的完整性(以下合称为“最后一公里服务”)也成为了消费者决定是否购买生鲜的关键影响因素。在“前置仓模式”下，最为消费者诟病的便是商品新鲜度不足和配送时效过慢，而二者都与“前置仓模式”下的生鲜电商(以下称“电商”)在保鲜和“最后一公里服务”过程中付出的努力水平密切相关。对于电商而言，冷链运输即是为了保持生鲜商品新鲜度，这一过程的成本与“最后一公里服务”的成本占据了其总成本的大部分比例。在成本压力下，如何激励电商做好商品保鲜服务并提高“最后一公里服务”的服务水平值得思考。
以上分析大多假设供应链各方不关注收益分配是否公平。然而，现实生活中，当供应链成员感受到不公平时，会采取措施改变现状，哪怕以牺牲自身利益为代价[9]。这种情况被称为公平关切现象。研究表明，公平关切现象同样存在于生鲜领域，并且生鲜领域中的公平关切现象会对生鲜商品的保鲜努力水平和生鲜供应链效用产生不利影响[10-12]。为了改进公平关切现象导致的效用损失，孙玉玲等[10]、张旭等[12]分别考虑用收益共享契约和改进的“自执行旁支付”契约协调供应链。然而，这些研究要么只考虑关系网络中某一方的公平关切现象，要么考虑的因素不够全面。具体来说，孙玉玲等[10]未考虑商品外在保鲜努力对新鲜度的影响；张庆等[11]未考虑如何解决公平关切下效用损失的问题；张旭等[12]仅考虑零售商公平关切下的情形。此外，现有文献的研究对象多为普通供应链，而鲜有学者关注“前置仓模式”下生鲜供应链的公平关切问题。在“前置仓模式”下，电商多采用“直采”的采购模式。“直采”供应商以农场、合作社、品牌商为主，这些供应商大多产品种类少，品牌知名度低，因此电商往往在零供关系中占据绝对主导地位。由于冷链运输和“最后一公里服务”环节的成本较高，为了维持一定的盈利水平，电商会压低采购价格，以弥补这两个环节的成本，拖欠供应商货款的行为也时有出现，这些行为都压低了供应商的生存空间，不利于保持供应链的稳定。虽然电商倒闭的报道频频出现，可是他们在分析其经营不善的原因时，往往都忽略了零供关系中，供应商合理利益诉求保障的缺失带来的重大不利影响。因此，供应链成员的公平关切是否影响电商的保鲜努力和“最后一公里服务”努力仍有待探索。
基于以上分析，本文构建由供应商和“前置仓模式”生鲜电商组成的二级生鲜供应链，用Nash讨价还价模型探讨公平关切对双方决策的影响，并考虑用“收益共享+成本分担”混合契约协调供应链，以实现供应链最优决策。
1. 问题描述与假设
1.1 问题描述
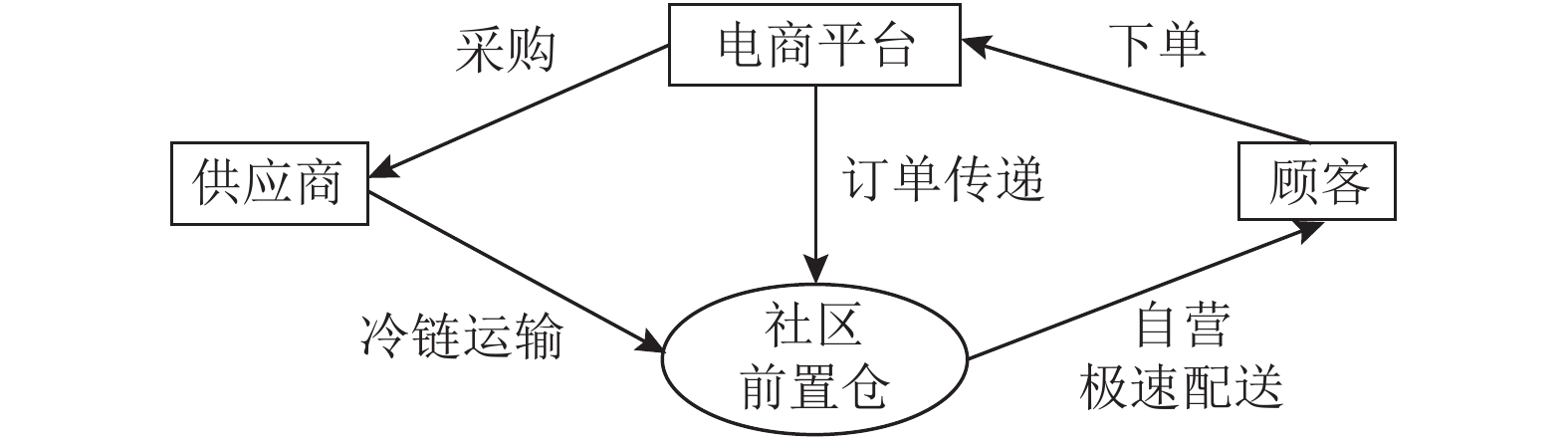
本文所研究的供应链运行模式如图1所示。电商平台向供应商发出采购请求，交易达成后，由电商通过自身冷链物流系统将生鲜商品运往社区前置仓，这一过程中，由电商决定为商品付出的保鲜努力水平。电商平台接到顾客的订单后，将订单传递至离顾客最近的社区前置仓，工作人员在社区前置仓将订单商品打包，由电商专有配送员将商品送达。在这一过程中，电商平台确定“最后一公里服务”努力水平。
![]()
图 1 “前置仓模式”生鲜供应链运行示意图Figure 1. The schematic diagram of fresh-product supply chain in “pre-position warehouse mode”1.2 研究假设
本文所涉及的参数及其含义的说明如表1所示。
表 1 模型参数及含义Table 1. Model parameters and implications参数 含义 π1、π2、π 分别表示供应商利润、电商利润、供应链总利润 U1、U2、U 分别为供应商效用、电商效用、供应链总效用 w 批发价格 p 零售价格 λ1、λ2(λi>0) 分别为供应商和电商公平关切系数 c1、c2 分别为供应商单位生产成本和电商单位可变成本 u1、u2 分别为电商保鲜努力成本系数和“最后一公里服务”努力成本系数 q 市场需求量 a 市场潜在需求量 b(b>0) 需求价格敏感系数 m、n(m、n>0) 分别为需求对保鲜努力和“最后一公里服务”努力敏感系数 e1、e2(ei>0) 分别为保鲜努力水平和“最后一公里服务”努力水平 下文表述中，右上标“*”表示一定条件下的最优决策；右下标“
c ”表示供应链集中决策；右下标“d ”表示公平中性下供应链分散决策；右下标“s”表示供应商公平关切下的决策；右下标“r ”表示电商公平关切下的决策；右下标“b ”表示供应链双方成员公平关切下的决策。假设1 参考文献[13-15]，成本是努力水平的二次函数。因此，假设保鲜努力成本
c(e1)=12u1e21 ，“最后一公里服务”努力成本c(e2)=12u2e22 。假设2 参考文献[5, 16]，需求与价格、新鲜度成正比，而新鲜度与保鲜努力水平成正比。因此，假设需求与保鲜努力水平成正比。此外，考虑到“前置仓模式”下“最后一公里服务”的重要性，假设需求与“最后一公里服务”努力水平成正比，即需求量
q=a−bp+me1+ne2 。假设3 为了使研究更具有一般性，假设
w＞c1,p＞w+c2 。假设4 基于文献[17-18]，假设需求对价格的敏感程度和保鲜努力成本系数乘积高于需求对保鲜努力敏感程度的平方(即
bu1＞m2 )，且需求对价格的敏感程度和“最后一公里服务”成本系数乘积高于需求对“最后一公里服务”敏感程度的平方(bu2＞n2 )，因此，有2bu1u2−u1n2−u2m2＞0 。2. 模型分析
2.1 供应链集中决策
集中决策下供应链利润为
πc=(p−c1−c2)(a−bp+me1+ne2)−12u1e21−12u2e22。 (1) 由式(1)可得，
πc 对p 、e1 和e2 的海塞矩阵行列式|H1|=|−2bmnm−u10n0−u2|=−2bu1u2+u1n2+u2m2＜0 ，且−2b＜0 ，2bu1−m2＞0 ，因此，πc 存在关于p、e1 和e2 的最大值。分别令
∂πc∂p=0，∂πc∂e1=0，∂πc∂e2=0 ，解得p∗c=au1u2+(bu1u2−mu2−nu1)(c1+c2)2bu1u2−m2u2−n2u1； e∗1c=mu2[a−b(c1+c2)]2bu1u2−m2u2−n2u1； e∗2c=nu1[a−b(c1+c2)]2bu1u2−m2u2−n2u1。 供应链总效用与最优利润相同，即
U∗c=π∗c=u1u2[a−b(c1+c2)]22(2bu1u2−m2u2−n2u1)。 2.2 公平中性假设下供应链分散决策
在分散决策下，双方利润函数为
π1=(w−c1)(a−bp+me1+ne2); (2) π2=(p−w−c2)(a−bp+me1+ne2)−12u1e21−12u2e22。 (3) 首先，电商根据利润最大化原则确定零售价p、保鲜努力水平
e1 和“最后一公里服务”努力水平e2 。由式(3)可得π2 对p、e1 和e2 海塞矩阵行列式|H2|=|H1|＜0 ，因此，π2 有关于p、e1 和e2 的最大值。分别令
∂π2∂p=0 ，∂π2∂e1=0 ，∂π2∂e2=0 ，得到p、e1 和e2 对w 的反应函数分别为p′d 、e′1d 、e′2d 。接着，供应商据此确定批发价以使自身利润最大化。将
p′d 、e′1d 和e′2d 代入式(2)，计算得∂2π1∂w2＜0 ，因此π1 存在最大值。令∂π1∂w=0 ，解得w∗d=a+b(c1−c2)2b 。将w∗d 代入p′d 、e′1d 和e′2d ，解得p∗d=2abu1u2+(bu1u2−mu2−nu1)[a+b(c1+c2)]2b(2bu1u2−m2u2−n2u1); e∗1d=mu2[a−b(c1+c2)]2(2bu1u2−m2u2−n2u1); e∗2d=nu1[a−b(c1+c2)]2(2bu1u2−m2u2−n2u1)。 将
w∗d 、p∗d 、e∗1d 和e∗2d 代入式(2)和式(3)可得π∗1d 、π∗2d 。同时，在公平中性情况下有U∗1d=π∗1d ，U∗2d=π∗2d ，U∗d=π∗d=π∗1d+π∗2d 。2.3 公平关切情形下供应链的决策
由于仅供应商公平关切和仅电商公平关切分别对应
λ2=0且λ1≠0 、λ1=0且λ2≠0 ，这两种情形可视为双方公平关切下的极端情况。因此，以下建模过程中，首先考虑双方公平关切的情形，再分别将电商和供应商公平关切系数赋值为零，从而研究仅某一方公平关切情形下的决策。参考文献[12]、[19]用Nash讨价还价最优解与实际利润的差异来刻画供应链成员对公平的感知。设Nash讨价还价下的最优解为(ˉπ1,ˉπ2) ，供应商和电商效用分别为U1=π1+λ1(π1−ˉπ1); (4) U2=π2+λ2(π2−ˉπ2)。 (5) 求解
maxπ1,π2U1U2 。s.t.π1+π2=π∗; ˉπ1+ˉπ2=π∗; U1＞0,U2＞0。 解得
ˉπ1=1+λ12+λ1+λ2π∗ ，ˉπ2=1+λ22+λ1+λ2π∗ 。分别将
ˉπ1 、ˉπ2 代入式(4)和式(5)得U1=(1+λ1)[(2+λ2)π1−λ1π2]2+λ1+λ2; (6) U2=(1+λ2)[(2+λ1)π2−λ2π1]2+λ1+λ2。 (7) 参考2.2节求解过程，由式(7)可得
U2 对p、e1 和e2 的海塞矩阵行列式为|H2|=(1+λ2)(2+λ1)2+λ1+λ2×|H1| ，且(1+λ2)(2+λ1)2+λ1+λ2＞0 ，因此，U2 有关于p、e1 和e2 的最大值。进一步解得w∗b=(2+λ1)2a+(λ1λ2+4λ2+2λ1+4)bc1−(2+λ1)2bc2(4+λ1)(2+λ1+λ2)b; p∗b=(4+λ1)abu1u2+(bu1u2−m2u2−n2u1)[(2+λ1)a+2b(c1+c2)](4+λ1)b(2bu1u2−m2u2−n2u1); e∗1b=2mu2[a−b(c1+c2)](4+λ1)(2bu1u2−m2u2−n2u1); e∗2b=2nu1[a−b(c1+c2)](4+λ1)(2bu1u2−m2u2−n2u1)。 将
w∗b 、p∗b 、e∗1b 和和e∗2b 代入式(2)、(3)、(6)、(7)，可得π∗1b=2u1u2(2+λ1)2[a−b(c1+c2)]2(4+λ1)2(2+λ1+λ2)(2bu1u2−m2u2−n2u1); π∗2b=2u1u2(λ1λ2+λ1+3λ2+2)[a−b(c1+c2)]2(4+λ1)2(2+λ1+λ2)(2bu1u2−m2u2−n2u1); U∗1b=2u1u2(1+λ1)[a−b(c1+c2)]2(4+λ1)(2+λ1+λ2)(2bu1u2−m2u2−n2u1); U∗2b=2u1u2(2+λ1)(1+λ2)[a−b(c1+c2)]2(4+λ1)2(2+λ1+λ2)(2bu1u2−m2u2−n2u1); U∗b=U∗1b+U∗2b=2u1u2(λ1λ2+λ12+6λ1+2λ2+6)[a−b(c1+c2)]2(4+λ1)2(2+λ1+λ2)(2bu1u2−m2u2−n2u1)。 将
λ2=0 代入w∗b 、e∗1b 、e∗2b 、π∗1b 、π∗2b 和U∗b ，可得仅供应商公平关切下的相关决策w∗s 、e∗1s 、e∗2s ，和决策效应π∗1s 、π∗2s 和U∗s 。将λ1=0 代入w∗b 、e∗1b 、e∗2b 、π∗1b 、π∗2b 和U∗b ，可得仅电商公平关切下的相关决策w∗r 、e∗1r 、e∗2r 和决策效应π∗1r 、π∗2r 、U∗r 。命题1 随着
λ1 的增大，w∗s 和w∗b 逐渐增大，e∗1s 和e∗2s 、e∗1b 和e∗2b 逐渐减小。证明 计算得
∂w∗s∂λ1＞0 ；∂w∗b∂λ1＞0 ；∂e∗1s∂λ1＜0 ；∂e∗2s∂λ1＜0 ；∂e∗1b∂λ1＜0 ；∂e∗2b∂λ1＜0 ，得证。命题1表明，随着供应商公平关切程度的增加，供应商参与讨价还价的愿望增强，将提出更高的批发价格。当电商考虑到供应商的公平关切行为时，批发价格会随着供应商公平关切程度的提高而上升，进而导致电商单位成本增加。电商为了维持利润会选择从其他方面节约成本，如降低保鲜努力水平和“最后一公里服务”努力水平，由此导致更低的商品新鲜度和“最后一公里服务”服务质量，大大降低了消费者体验，使得消费者利益受损。
命题2 随着
λ2 的增大，w∗r 和w∗b 逐渐减小，而e∗1r 和e∗2r 、e∗1b 和e∗2b 与λ2 无关。证明 计算得
∂w∗r∂λ2＜0 ；∂w∗b∂λ2＜0 。由上文计算结果可知，e∗1r 和e∗2r 、e∗1b 和e∗2b 的表达式不含λ2 ，得证。命题2表明，随着电商的公平关切程度逐渐增加，其不会降低保鲜努力水平和“最后一公里服务”努力水平。因此，在仅电商公平关切的情形下，保鲜努力水平和“最后一公里服务”努力水平决策与公平中性分散决策情形下对应的最佳决策相等。在供应链双方公平关切的情形下，保鲜努力水平和“最后一公里服务”努力水平与仅供应商公平关切情形下对应的最佳决策相等。然而，电商过度的公平关切将会使供应商利益受损。因为随着电商公平关切程度
λ2 的逐渐增加，电商会不断压低向供应商的采购价格，以获取更高的渠道利润。一旦供应商难以接受较低的批发价时，可能会拒绝与电商合作，从而出现“市民买不到，农民卖不出”的怪象。命题3 随着供应商公平关切程度的增加，供应商与电商的利润比逐渐升高；随着电商公平关切程度的增加，供应商与电商的利润比逐渐降低。
证明 计算得
π∗1sπ∗2s=2+λ1=f(λ1) ，f′(λ1)＞0 ；π∗1rπ∗2r=43λ2+2=g(λ2) ，g′(λ2)＜0 ；π∗1bπ∗2b=(2+λ1)2λ1λ2+λ1+3λ2+2=h(λ1,λ2) ，∂h(λ1,λ2)∂λ1＞0 ，∂h(λ1,λ2)∂λ2＜0 ，得证。命题3表明，随着供应商公平关切程度的增加，其渠道利润占比也逐渐提高，与此同时，电商的渠道利润占比逐渐降低。反之，随着电商公平关切程度的增加，供应商的渠道利润占比逐渐降低，而电商的渠道利润占比逐渐升高。因此，增大自身渠道利润占比可以看作供应链成员公平关切的直接体现。这也与现实中一致，供应链成员的谈判愿望越强烈，其更有可能获得更高比例的渠道收益。
命题4
e∗1b=e∗1s＜e∗1r=e∗1d＜e∗1c ；e∗2b=e∗2s＜e∗2r=e∗2d＜e∗2c ；max(U∗s,U∗r,U∗b)＜U∗d＜U∗c 。证明 由命题2可得
e∗1b=e∗1s ；e∗1r=e∗1d ；e∗2b=e∗2s ；e∗2r=e∗2d ；同时计算得e∗1de∗1c=12＜1 ，e∗1be∗1d=44+λ1＜1 ；e∗2de∗2c=12＜1 ；e∗2be∗2d=44+λ1＜1 。因此，e∗1b=e∗1s＜e∗1r=e∗1d＜e∗1c ；e∗2b=e∗2s＜e∗2r=e∗2d＜e∗2c 。U∗dU∗c=34＜1 ；U∗sU∗d=16λ12+96λ1+963λ13+30λ12+96λ1+96＜1 ；U∗rU∗d=2λ2+63λ2+6＜1 ；U∗bU∗d=16λ1λ2+16λ12+96λ1+32λ2+9624λ1λ2+30λ12+96λ1+48λ2+96+3λ13+3λ12λ2＜1 。因此，max(U∗s,U∗r,U∗b)＜U∗d＜U∗c ，得证。命题4表明，在供应商公平关切情形下，电商的保鲜努力水平和“最后一公里服务”努力水平偏低，以及供应商或电商公平关切情形下供应链总效用的损失的原因可以归纳为两个方面。一方面是由于公平关切方为提升自身渠道利润占比而直接或间接导致商品新鲜度低和“最后一公里服务”质量差，从而最终损害消费者利益；另一方面则是因为在分散决策下，供应商和电商均以效用最大化原则决策，从而导致双重边际效应效用损失。因此，无论从电商保鲜努力水平和“最后一公里服务”努力水平方面来看，还是从供应链总效用方面来讲，当供应链成员存在公平关切时，系统未达帕累托最优。
2.4 公平关切情形下供应链的协调机制
基于以上分析，为了达到系统帕累托最优，电商需要付出更多保鲜努力和“最后一公里服务”努力，电商的成本将增加，因此，供应商有必要分担部分电商成本。同时，生鲜电商将部分收益与供应商分享，以使供应商有分担成本的动力，从而达到供应链稳定状态。本文考虑用由“收益共享契约+成本分担契约”这一混合契约(
w0,φ1,φ2 )协调供应链。其中，φ1 为收益共享系数，φ2 为成本分担系数。需要说明的是，由于仅供应商公平关切情形和仅电商公平关切情形可以视为双方公平关切情形下的特殊情况，本文仅讨论双方公平关切情形下供应链的协调。命题5 当满足
{w0=[(2+λ1)(1−φ1)−λ2φ1](c1+c2)+λ2c1−(2+λ1)c22+λ1+λ2;(2+λ1)2(4+λ1)(2+λ1+λ2)⩽φ1=φ2⩽[(4+λ1)2−4](2+λ1)(4+λ1)2(2+λ1+λ2) 时，供应链可实现协调。证明 建立混合契约后，供应商和电商的利润分别为
π′1=(w0−c1+φ1p)(a−bp+me1+ne2)−φ2(12u1e21+12u2e22); π′2=[(1−φ1)p−w0−c2](a−bp+me1+ne2)−(1−φ2)×(12u1e21+12u2e22)。 电商和供应商的效用函数分别为
U′1=(1+λ1)[(2+λ2)π′1−λ1π′2]2+λ1+λ2; (8) U′2=(1+λ2)[(2+λ1)π′2−λ2π′1]2+λ1+λ2。 (9) 由式（9）解得
U′2 对p 、e1 和e2 的海塞矩阵行列式为|H3|=(1+λ2)[(2+λ1)−(2+λ1+λ2)φ1]2+λ1+λ2×|H1|。 当
(1+λ2)[(2+λ1)−(2+λ1+λ2)φ1]2+λ1+λ2＞0 ，即φ1＜2+λ12+λ1+λ2 时，|H3|＜0，U′2 有关于p、e1 和e2 的最大值。分别令
∂U′2∂p=0 ；∂U′2∂e1=0 ；∂U′2∂e2=0 ，得到p、e1 和e2 关于w的反应函数分别为p″ 、e″1 、e″2 。若达到系统帕累托最优，需要有p″=p∗c ；e″1=e∗1c ；e″2=e∗2c ，解得{φ1=φ2;w0=[(2+λ1)(1−φ1)−λ2φ1](c1+c2)+λ2c1−(2+λ1)c22+λ1+λ2。 (10) 将式(10)代入式(8)和式(9)，并且令
φ1=φ2=φ ，可得协调后双方的最大效用分别为U′∗1 和U′∗2 。供应链协调后，供应商和电商获得的效用应不小于协调前各自的效用，也即
{U′∗1⩾U∗1bU′∗2⩾U∗2b ，同时应满足φ1＜2+λ12+λ1+λ2 。解得φ 的取值范围为(2+λ1)2(4+λ1)(2+λ1+λ2)⩽φ⩽[(4+λ1)2−4](2+λ1)(4+λ1)2(2+λ1+λ2) ，得证。3. 数值分析
本文涉及参数设定见表2。
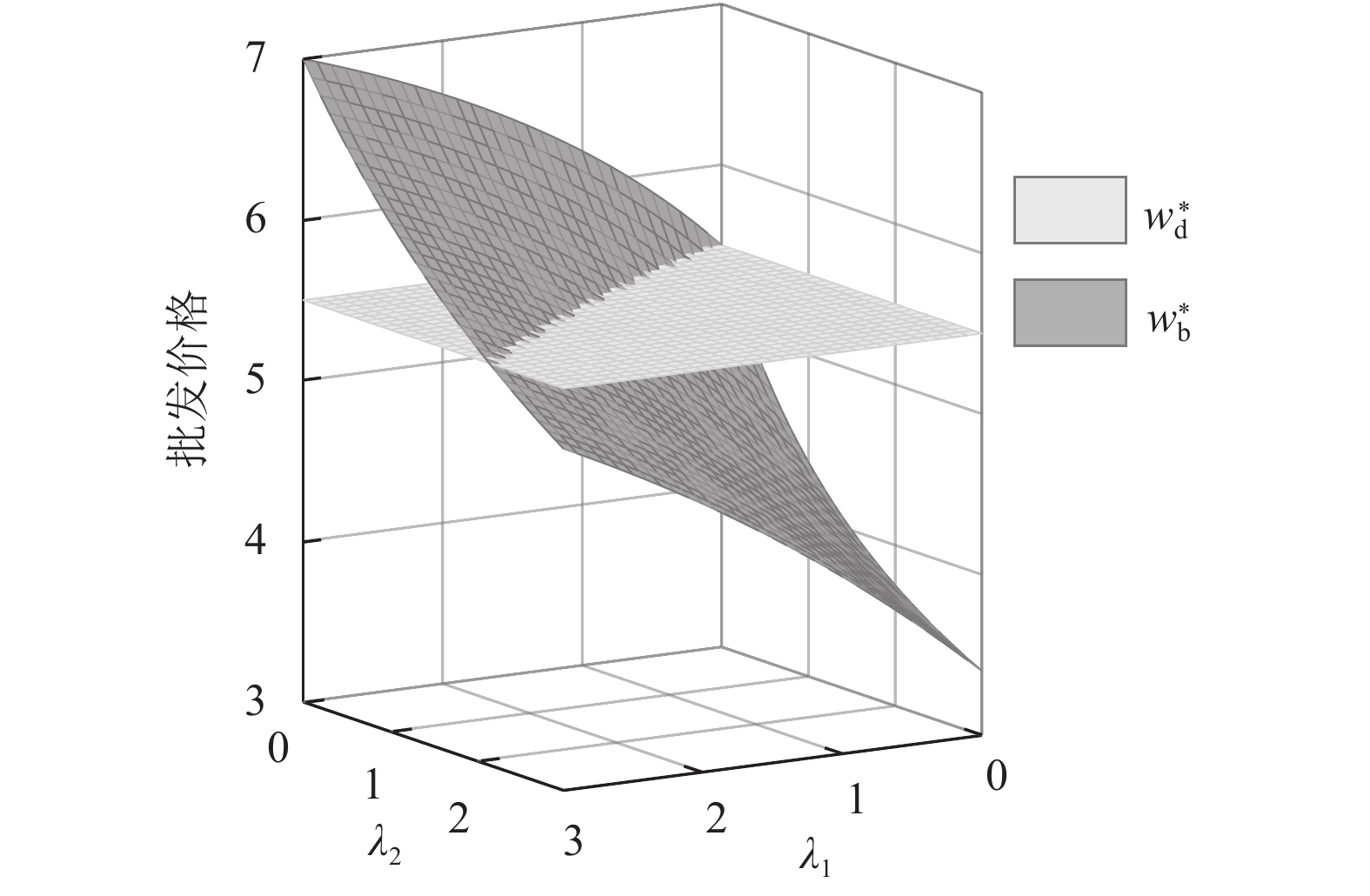
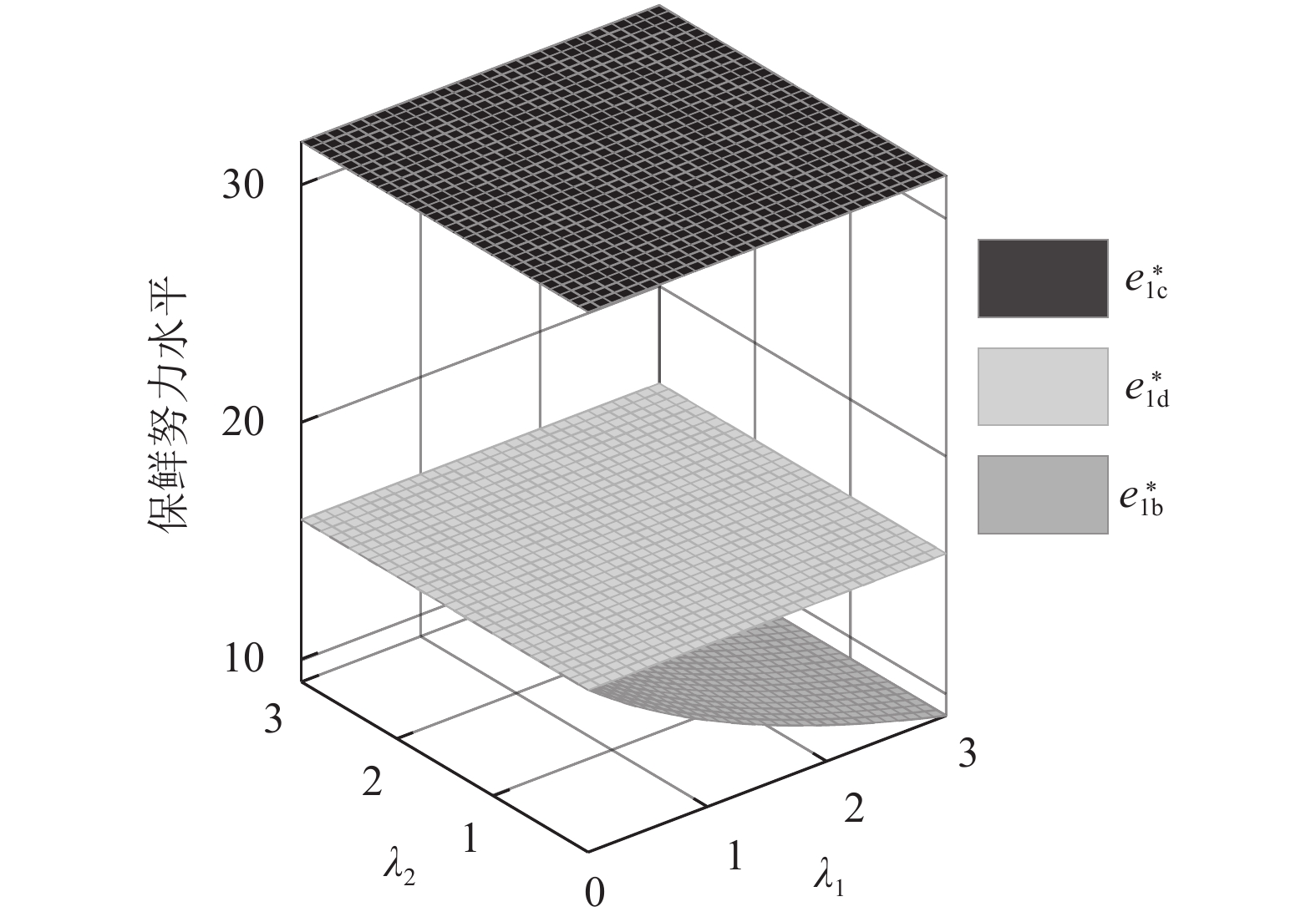
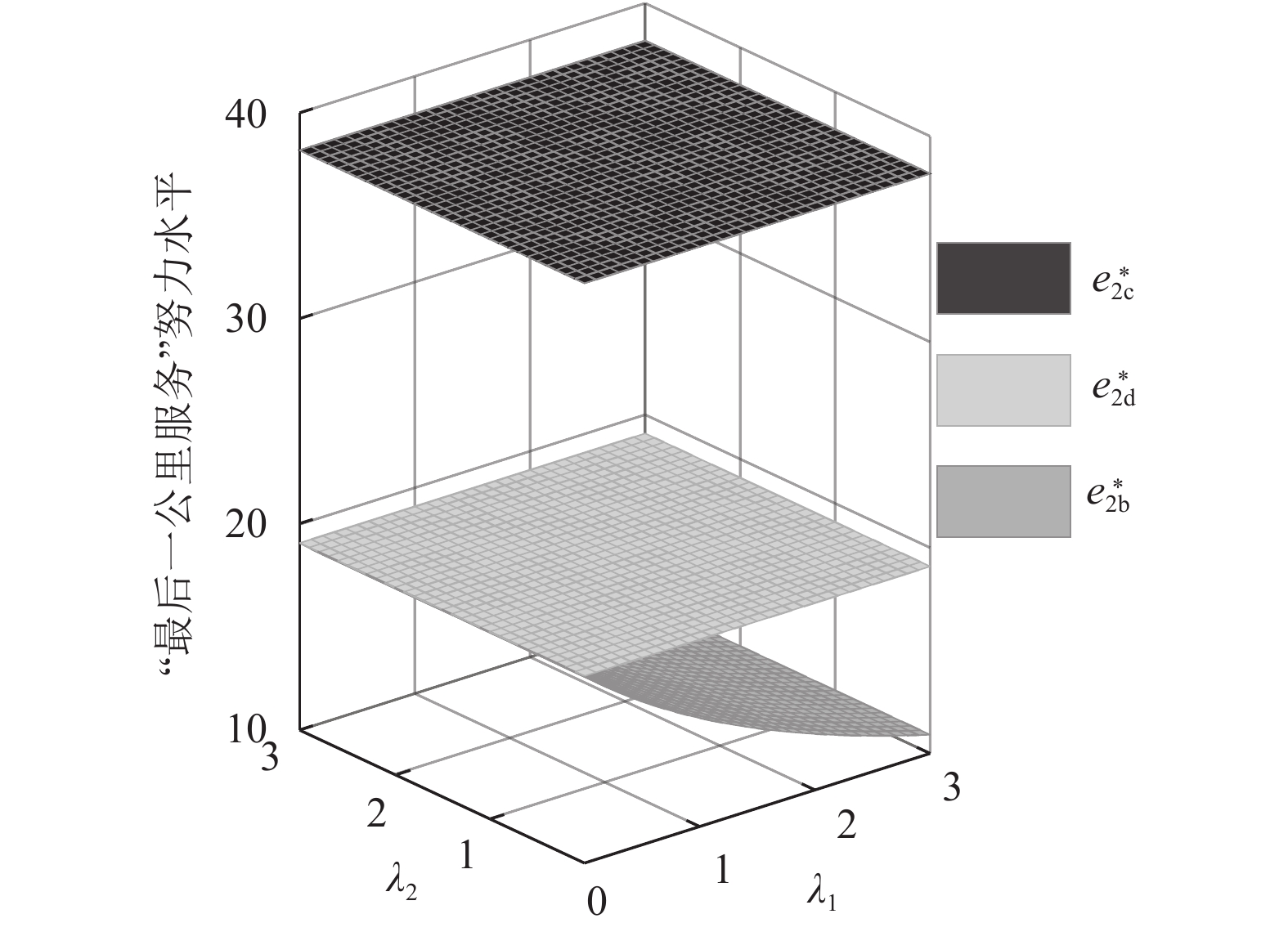
表 2 数值分析参数设定Table 2. The given values of model parametersa b m n u1 u2 c1 c2 100 10 5 4 3 2 2 1 图2~4反映了公平关切对相关决策的影响。由图2可以看出，供应商的公平关切总是倾向于提高批发价格，电商则反之。图3和图4显示，电商的最优保鲜努力水平和“最后一公里服务”努力水平会受供应商公平关切影响而低于公平中性下的决策，但与电商的公平关切无关。图2~4与命题1、2中的结论一致。
![]()
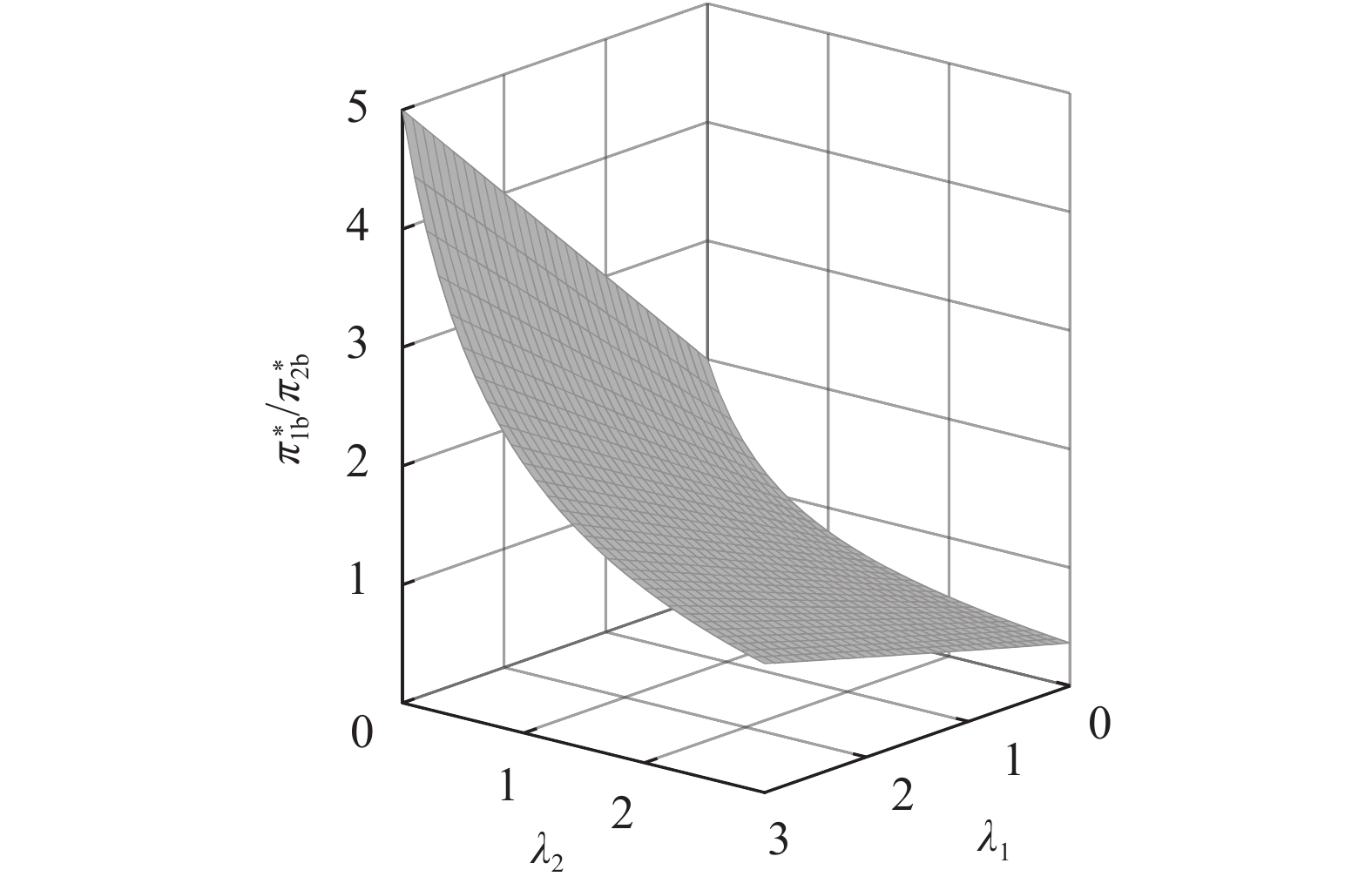
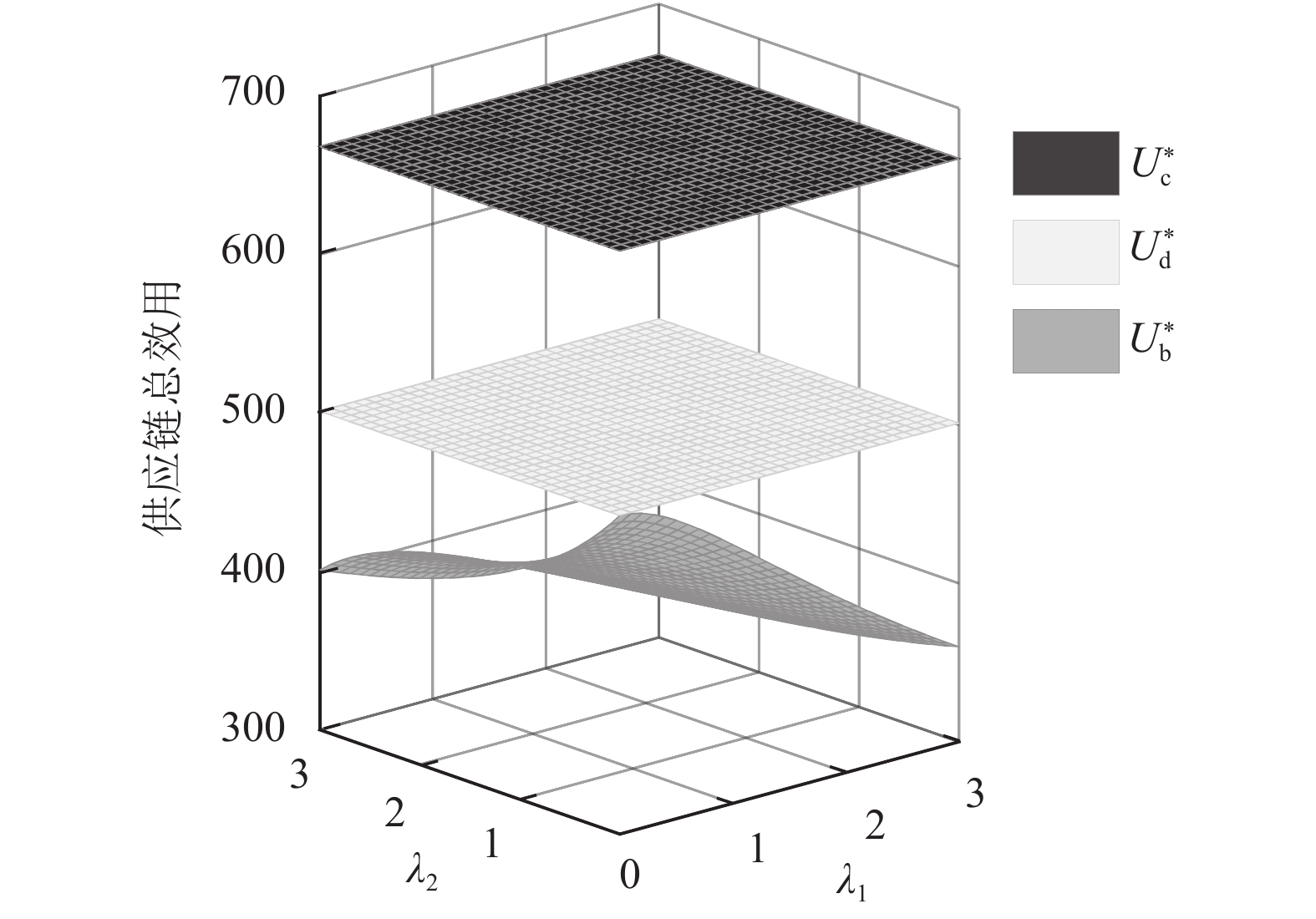
图 4 公平关切对“最后一公里服务”努力水平的影响Figure 4. The effect of fairness concern on “last kilmeter service” efforts图5和图6反映了公平关切对双方利润比及供应链总效用的影响。由图5可以看出，在其他条件一定时，供应商或电商的渠道收益比会随其自身的公平关切程度增加而增大，与命题3中的相关结论一致。图6表明，当存在供应链成员公平关切时，供应链的总效用总是小于供应链成员公平中性时供应链总效用。其中，公平中性集中决策下供应链总效用最高，公平中性分散决策下供应链总效用次之，供应链成员存在公平关切情况下供应链总效用最低，从而说明公平关切会导致双重边际效应和非理性决策带来的效用损失，与命题4中的结论一致。
![]()
图 5 公平关切对供应商与电商利润比的影响Figure 5. The effect of fairness concern on earning ratio of supplier to online retailer![]()
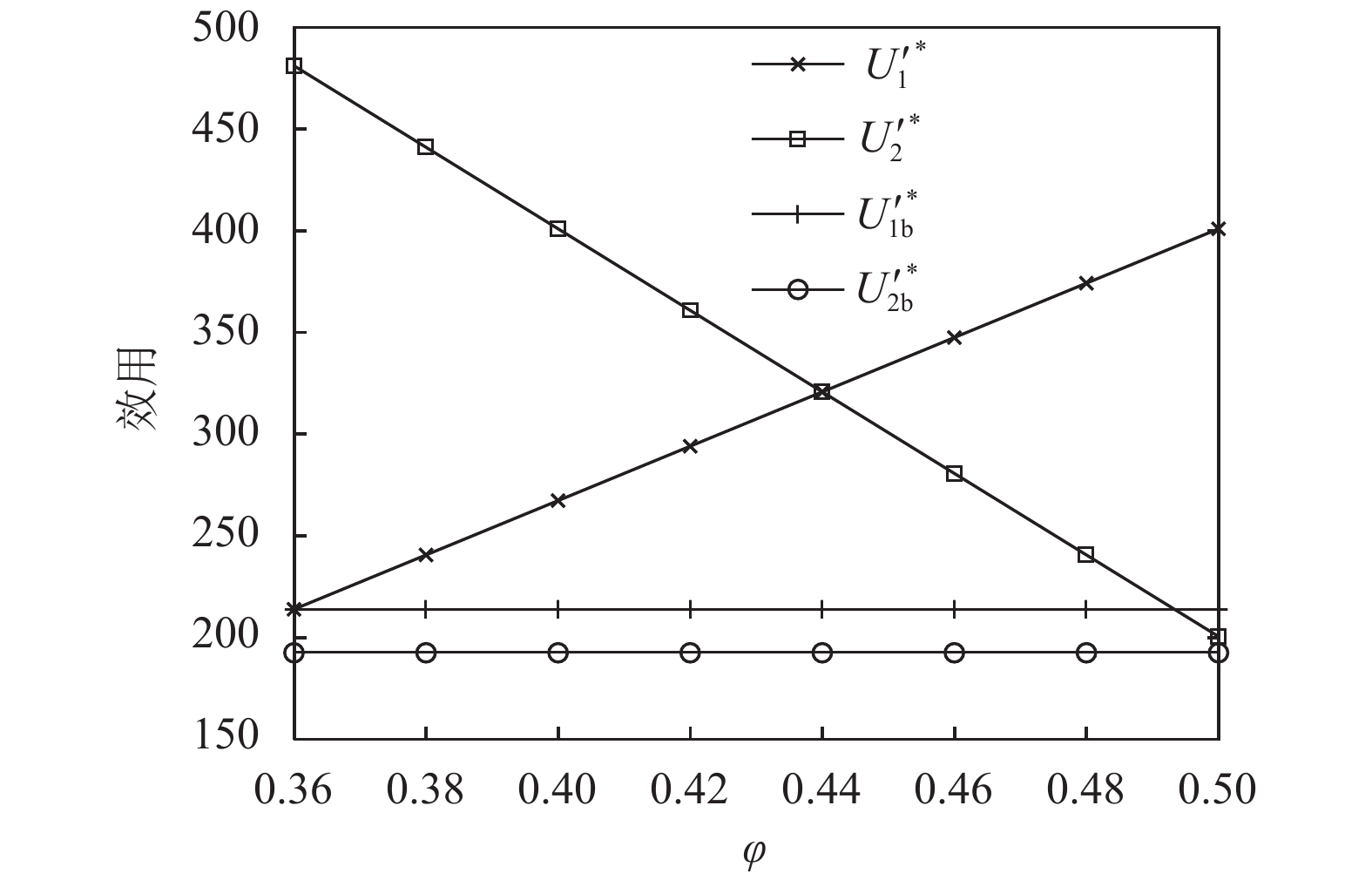
图 6 公平关切对供应链总效用的影响Figure 6. The effect of fairness concern on total supply chain utility为了验证混合契约的有效性，令
λ1 =1，λ2 =2，计算并描绘收益共享和成本分担系数对供应链协调前后供应商和电商效用的影响，如图7所示。由图7可以看出，在给定的收益共享和成本分担系数范围内，供应链协调后，双方的效用均得到提升。图7验证了命题5。![]()
图 7 收益共享与成本分担系数对供应链总效用的影响Figure 7. The effect of earnings and cost sharing coefficient on total supply chain utility4. 结论与启示
本文分析由生鲜产品供应商和“前置仓模式”生鲜电商组成的二级供应链的博弈。研究结果表明，在公平关切心理的驱动下，供应商和电商均倾向于提升自身的渠道收益比，对高渠道收益比的追逐可能导致供应链主体作出非理性决策。具体表现如下。1) 在供应商公平关切时，供应商会要求更高批发价格，电商的反应是降低保鲜努力水平以及“最后一公里服务”努力水平，从而导致商品新鲜度更低、服务更差。2) 在电商公平关切时，电商会压低批发价格，当作为供应链弱势群体的供应商合理的要价不能得到满足时，供应链的合作将受到威胁。以上非理性决策会造成供应链效用的损失，不利于供应链的稳定。然而，这一供应链失效可以通过 “收益共享+成本分担”混合契约得到解决，通过实施混合契约，电商将提高保鲜努力水平和“最后一公里服务”努力水平，供应链双方的效用均实现帕累托改进。
针对公平关切下供应商和电商的非理性决策问题，本文得到以下启示。1) 对电商而言，管理层在制定决策时，不能过度追求公平，否则可能造成合作不稳定甚至合作破裂，从而使得自身和供应链利益受损。电商在制定供应商条款时，应适度考虑供应商利益，减少或杜绝附加收费、长账期行为，以创造良好的合作环境。2) 对于供应商而言，弱势供应商群体可以组建成农业合作社或者企业联盟，以增大自身规模和实力，提高谈判地位，使合理公平的诉求得到满足。3) 对供应链双方而言，各方均应转换思维模式，创新合作机制。供应商与电商之间在合作时，应考虑如何实现正和博弈而非零和博弈。例如，通过供应链契约的设置，使得供应链双方成为利益共同体，从而站在供应链整体层面作出决策，以保证为目标消费者提供优质的生鲜商品和“最后一公里服务”的同时提高各方效用，实现共赢。4) 对政府而言，一方面应加强对生鲜电商企业的监管，督促其提供新鲜的生鲜商品和高效的服务，合理保障消费者的利益；另一方面可以考虑对生鲜电商提供补贴，以部分弥补电商高额的保鲜成本和“最后一公里服务”成本，促进“前置仓模式”下生鲜电商的蓬勃发展。
-
![]()
图 1 “前置仓模式”生鲜供应链运行示意图
Figure 1. The schematic diagram of fresh-product supply chain in “pre-position warehouse mode”
![]()
图 4 公平关切对“最后一公里服务”努力水平的影响
Figure 4. The effect of fairness concern on “last kilmeter service” efforts
![]()
图 5 公平关切对供应商与电商利润比的影响
Figure 5. The effect of fairness concern on earning ratio of supplier to online retailer
![]()
图 6 公平关切对供应链总效用的影响
Figure 6. The effect of fairness concern on total supply chain utility
![]()
图 7 收益共享与成本分担系数对供应链总效用的影响
Figure 7. The effect of earnings and cost sharing coefficient on total supply chain utility
表 1 模型参数及含义
Table 1 Model parameters and implications
参数 含义 π1、π2、π 分别表示供应商利润、电商利润、供应链总利润 U1、U2、U 分别为供应商效用、电商效用、供应链总效用 w 批发价格 p 零售价格 λ1、λ2(λi>0) 分别为供应商和电商公平关切系数 c1、c2 分别为供应商单位生产成本和电商单位可变成本 u1、u2 分别为电商保鲜努力成本系数和“最后一公里服务”努力成本系数 q 市场需求量 a 市场潜在需求量 b(b>0) 需求价格敏感系数 m、n(m、n>0) 分别为需求对保鲜努力和“最后一公里服务”努力敏感系数 e1、e2(ei>0) 分别为保鲜努力水平和“最后一公里服务”努力水平 
下载: 导出CSV
-
[1] CAI X, CHEN J, XIAO Y, et al. Fresh-product supply chain management with logistics outsourcing[J]. Omega, 2013, 41(4): 752-765. DOI: 10.1016/j.omega.2012.09.004
[2] WU Q, MU Y, FENG Y. Coordinating contracts for fresh product outsourcing logistics channels with power structures[J]. International Journal of Production Economics, 2015, 160: 94-105. DOI: 10.1016/j.ijpe.2014.10.007
[3] 王道平, 李昕怡, 张博卿. 考虑两阶段价格的生鲜农产品供应链协调研究[J]. 工业工程与管理, 2016, 21(5): 16-22. DOI: 10.3969/j.issn.1007-5429.2016.05.003 WANG Daoping, LI Xinyi, ZHANG Boqing. Study on coordination of fresh agricultural products supply chain based on two-phase pricing[J]. Industrial Engineering and Management, 2016, 21(5): 16-22. DOI: 10.3969/j.issn.1007-5429.2016.05.003
[4] 曹裕, 李业梅, 万光羽. 基于消费者效用的生鲜农产品供应链生鲜度激励机制研究[J]. 中国管理科学, 2018, 26(2): 160-174. CAO Yu, LI Yemei, WAN Guangyu. Study on the fresh degree incentive mechanism of fresh agricultural product supply chain based on consumer utility[J] Chinese Journal of Management Science, 2018, 26(2): 160-174.
[5] 王道平, 朱梦影, 王婷婷. 考虑时间约束的生鲜供应链保鲜努力成本分担契约研究[J/OL]. (2019-07-24). https://kns.cnki.net/kcms/detail/31.1738.T.20190724.1215.012.html. [6] 史保阳, 史保莉. 考虑努力水平与损耗的农超对接生鲜产品供应链协调[J]. 工业工程与管理, 2019, 24(5): 43-48, 55. SHI Baoyang, SHI Baoli. Fresh agricultural product supply chain coordination considering the level of effort and the loss[J]. Industrial Engineering and Management, 2019, 24(5): 43-48, 55.
[7] ZHENG Q, IEROMONACHOU P, FAN T, et al. Supply chain contracting coordination for fresh products with fresh-keeping effort[J/OL]. (2017-04-10). https://www.emerald.com/insight/content/doi/10.118/IMDS-04-2016-0139/full/html.
[8] SONG Z, HE S. Contract coordination of new fresh produce three-layer supply chain[J]. Industrial Management & Data Systems, 2019, 119(1): 148-169.
[9] CUI H, JAGMOHAN S R, ZHANG Z. Fairness and channel coordination[J]. Management Science, 2007, 53(8): 1303-1314. DOI: 10.1287/mnsc.1060.0697
[10] 孙玉玲, 洪美娜, 石岿然. 考虑公平关切的鲜活农产品供应链收益共享契约[J]. 运筹与管理, 2015, 24(6): 103-111. SUN Yuling, HONG Meina, SHI Kuiran. Revenue sharing contract of supply chain for fresh agricultural products considering fairness concerns[J]. Operations Research and Management Science, 2015, 24(6): 103-111.
[11] 张庆, 张旭. 不同公平关切行为下的生鲜农产品供应链定价策略[J]. 系统工程, 2016, 34(9): 93-100. ZHANG Qing, ZHANG Xu. Pricing strategy of fresh agricultural supply chain under different behaviors of fairness concerns[J]. Systems Engineering, 2016, 34(9): 93-100.
[12] 张旭, 张庆. 零售商公平关切下的生鲜品供应链协调机制[J]. 系统工程学报, 2017, 32(4): 461-473. ZHANG Xu, ZHANG Qing. Coordination mechanism for fresh agricultural supply chain under the retailer's fairness concerns[J]. Journal of Systems Engineering, 2017, 32(4): 461-473.
[13] CHINTAGUNTA P K, JAIN D. A dynamic model of channel member strategies for marketing expenditures[J]. Marketing Science, 1992, 11(2): 168-188. DOI: 10.1287/mksc.11.2.168
[14] MOON I, JEONG J Y, SAHA S. Investment and coordination decisions in a supply chain of fresh agricultural products[DB/OL]. (2018-06-06). https://link.springer.com/article/10.1007/s12351-018-0411-4.
[15] SONG H, GAO X. Green supply chain game model and analysis under revenue-sharing contract[J]. Journal of Cleaner Production, 2018, 170: 183-192. DOI: 10.1016/j.jclepro.2017.09.138
[16] YU Y, XIAO T. Pricing and cold-chain service level decisions in a fresh agri-products supply chain with logistics outsourcing[J]. Computers & Industrial Engineering, 2017, 111: 56-66.
[17] YANG L, TANG R. Comparisons of sales modes for a fresh product supply chain with freshness-keeping effort[J]. Transportation Research Part E: Logistics and Transportation Review, 2019, 125: 425-448. DOI: 10.1016/j.tre.2019.03.020
[18] 曹裕, 刘培培, 胡韩莉. 基于成本共担契约的生鲜供应链保鲜努力机制研究[J]. 控制与决策, 2019, 35(1): 1-10. CAO Yu, LIU Peipei, HU Hanli. Freshness efforts mechanism of fresh-keeping supply chain based on cost sharing contract[J]. Control and Decision, 2019, 35(1): 1-10.
[19] 杜少甫, 朱贾昂, 高冬, 等. Nash讨价还价公平参考下的供应链优化决策[J]. 管理科学学报, 2013, 16(3): 68-72. DU Shaofu, ZHU Jiaang, GAO Dong, et al. Optimal decision-making for Nash bargaining fairness concerned newsvendor in two-level supply chain[J]. Journal of Management Sciences in China, 2013, 16(3): 68-72.
-
期刊类型引用(3)
1. 周琪. 新零售背景下山姆会员商店运营模式探析. 商展经济. 2023(06): 92-94 . 
百度学术
2. 罗云伟. 我国生鲜农产品供应链发展策略研究. 物流工程与管理. 2023(04): 76-78 . 百度学术
3. 毛洁. 生鲜农产品前置仓电商模式发展策略探讨. 商业经济研究. 2022(18): 94-97 . 百度学术
其他类型引用(19)
计量
- 文章访问数: 1321
- HTML全文浏览量: 38
- PDF下载量: 4833
- 被引次数: 22
