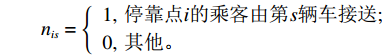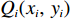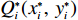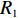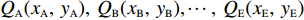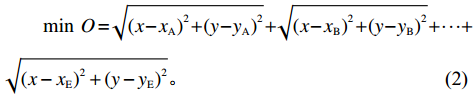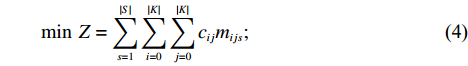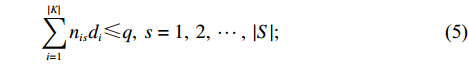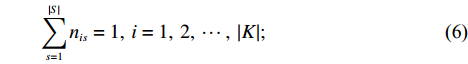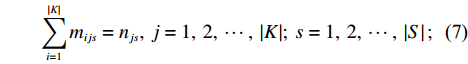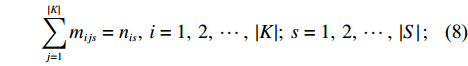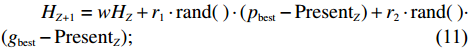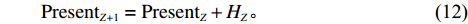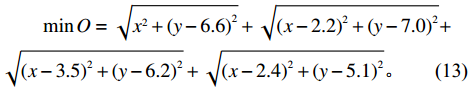随着我国经济的飞速发展，汽车消费迅猛上升，交通拥堵成为我国城市发展常态问题，而且呈现愈演愈烈的趋势。《2019年中国城市交通报告》中指出，集中出行尤其是高峰期通勤，选择私家车等道路利用率低的出行模式是大多数城市交通拥堵的重要成因^[1]。公共交通方式由于站点、路线固定，选择其进行通勤往往会在绕行、等待和转乘上花费大量时间，而城市节奏的不断加快又使人们对通勤效率的要求越来越高，城市公共交通与人们的通勤需求之间存在着较大的矛盾。部分企业为职工开通通勤车，意在缓解职工“通勤难”问题，然而由于员工居住地分散，缺乏合理的路线规划，难以满足上班族的通勤需求导致其乘坐率很低。因此许多上班族选择私家车通勤，高峰期城市交通压力不断增大。在这种背景下，本文研究通勤车动态路径优化问题，改变传统企业通勤车路线固定的模式，对提高上班族通勤效率，缓解高峰期城市交通拥堵具有较强的现实意义。

本文在优化通勤车路径时借鉴运筹学中的VRP (vehicle routing problem，车辆路径问题)。VRP被大多数学者用于物流配送车辆路径问题上，有学者注意到VRP同样适用于载人的车辆路径问题上，因此SBRP (school bus routing problem，校车路径问题)也得到了一定的发展。VRP中包含着许多的分支，DVRP (dynamic vehicle routing problem，动态车辆路径问题)就是其中常见的一种，由Psaraftis^[2]教授总结提出，之后Bertsimas等^[3]、Gendreau等^[4]针对DVRP的内容作了深入的研究，Azi等^[5]指出DVRP的动态因素主要分为两个方面，一个是顾客需求的变化；另一个是交通路况的变化。随着物联网、全球定位系统等的进步，实时获取路况信息变得越来越容易，因此基于实时交通信息的DVRP也获得发展的契机，这类问题一般都分解为初始路径设计和动态调整路线两个问题来求解。国内外学者对此的研究主要集中在路线更新规则和优化算法上。关于路线更新规则主要有4种。Kilby等^[6]、Abdallah等^[7]、张文博等^[8]均利用定期更新策略解决DVRP，车辆每隔一段时间更新一次路线，核心思想是将动态路径转化为静态路径。Armas等^[9]利用动态事件更新策略解决DVRP问题，一旦接收到新的动态路况信息就更新路线。Nakamura等^[10]利用顾客处更新策略解决DVRP，车辆行驶到停靠点更新一次路线。Chen等^[11]、李妍峰等^[12]利用关键点更新策略解决DVRP，车辆在停靠点、拥堵易发生点等关键点调整路径，其重点在于对“关键点”的定义。关于优化算法的研究更加丰富，主要有精确算法和启发式算法两种。由于研究数据量的不断扩大和对求解效率要求的提高，启发式算法是当下的研究热点，常见的有禁忌搜索算法、蚁群算法、遗传算法、粒子群算法等。Ozbaygin等^[13]设计并行禁忌搜索算法，并用其解决一个迭代再优化结构的动态车辆路径问题。蔡婉君等^[14]利用蚁群算法对9个经典算例实验证明蚁群算法针对车辆路径问题的有效性。孙小军等^[15]设计一种改进蚁群算法来求解双目标带时间窗的动态车辆路径问题。Zheng等^[16]结合蚁群算法和遗传算法构建RHC，并通过10个DVRP的案例证实其有效性。Yigit等^[17]将蚁群算法和遗传算法结合来实时优化动态校车路径问题。Abdallah等^[7]利用遗传算法解决需求和路况信息都不断变化的VRP。Okulewicz等^[18]将DVRP作为测试问题，比较离散编码的遗传算法与微分进化算法的求解效率和稳定性。Barkaoui等^[19]对遗传算子进行改进，得到自适应混合遗传算法，可以大幅度提高遗传算法解的质量。张亚明等^[20]设计改进的经营单亲遗传算法来求解VRP。Okulewicz等^[21]提出两阶段粒子群算法，很好地解决动态需求的VRP。陈玉光^[22]改进粒子群算法，准确地求解了基于准时送货和成本最小的VRP模型。胡小宇等^[23]对传统粒子群算法进行改进解决单仓储多车物流配送路径优化问题。陈久梅等^[24]利用粒子群算法求解冷链配送车辆路径问题并证明了粒子群算法具有很好的收敛性。

通过对文献资料的分析可知，基于实时交通信息的DVRP是当下的研究热点，国内外学者对其的研究重点大多是路线更新规则，而车辆路径问题属于NP-hard问题，一些在收敛性上比较好的算法被广泛使用，如粒子群算法、蚁群算法、遗传算法等。同时，有学者发现了选址问题和车辆路径问题的相关性。李宏光等^[25]指出站点配置是路径规划的约束和前提，通勤车站点配置方案将会直接影响路径规划。但现有的研究很少有将停靠点选址问题和车辆路径问题相结合，为此本文首先就如何为通勤车停靠点选址最为合理进行分析，通过解决初始路径设计和动态调整路线两个部分来完成对通勤车的动态路径优化，在最优的初始路径基础上选择关键点更新策略作为路线更新规则，并重新定义实际交通中的关键点，指出具体的路线更新方式，从而找到基于实时交通信息的通勤车最优路径。

1.   问题描述

停靠点是通勤车路径网络中的重要节点，其选址的结果会对优化后的路径优劣产生一定的影响，因此本文在路径优化前先对停靠点选址问题进行研究。分析当下城市布局，上班族的居住地点大多呈现出离散化分布的特点，许多通勤车在接送上班族时往往就近选择停靠点，导致通勤车需要长时间绕行，优先上车或靠后下车的乘客会产生较多时间上的沉没成本。本文将停靠点选址纳入优化范围，通过已知的数个员工住址点确定一个未知的地点，选址的过程以距离最短作为目标，以欧氏距离作为标准，与实际距离会有所差异，本文假设员工住址与选择的停靠点之间不需要过多绕行，使用欧氏距离对实际结果影响不大。

本文将通勤车的动态路径优化问题划分为初始路径设计和动态路线调整进行解决，在初始路径设计时需要考虑到现实中的交通路网是复杂的，两个地点之间往往有多条路线，设计初始路径是在理想状态下进行的，以路径最短的路线作为通勤效率最高的路线。假设：

1) 初始路径设计时每条路径的路况相同，没有外界因素干扰车辆行驶速度；

2) 多辆车重复经过同一停靠点的成本远高于未满载的成本，不能出现多辆车接送一个停靠点乘客的情况。

影响动态路径优化的因素有动态的顾客需求和动态的路况变化。本文的研究只集中于动态的路况，即通过实时交通信息动态调整路线。假设：

1) 某一时间段内停靠点的乘客人数一旦确定就不会发生变化，即不考虑乘客需求量动态变化的情况；

2) 可以根据路况信息大致判断出通过每条路线需要花费的时间。

2.   模型建立

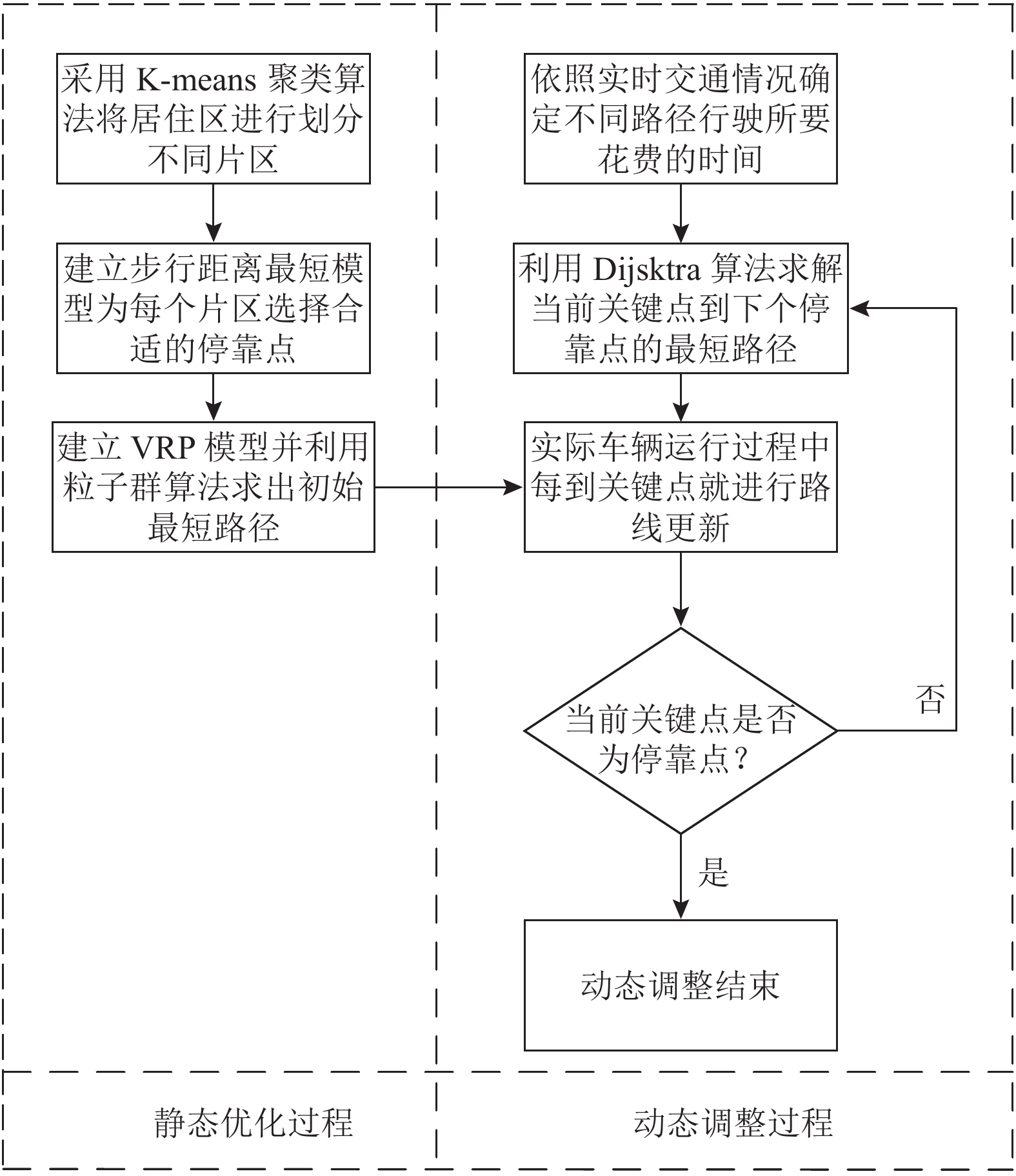
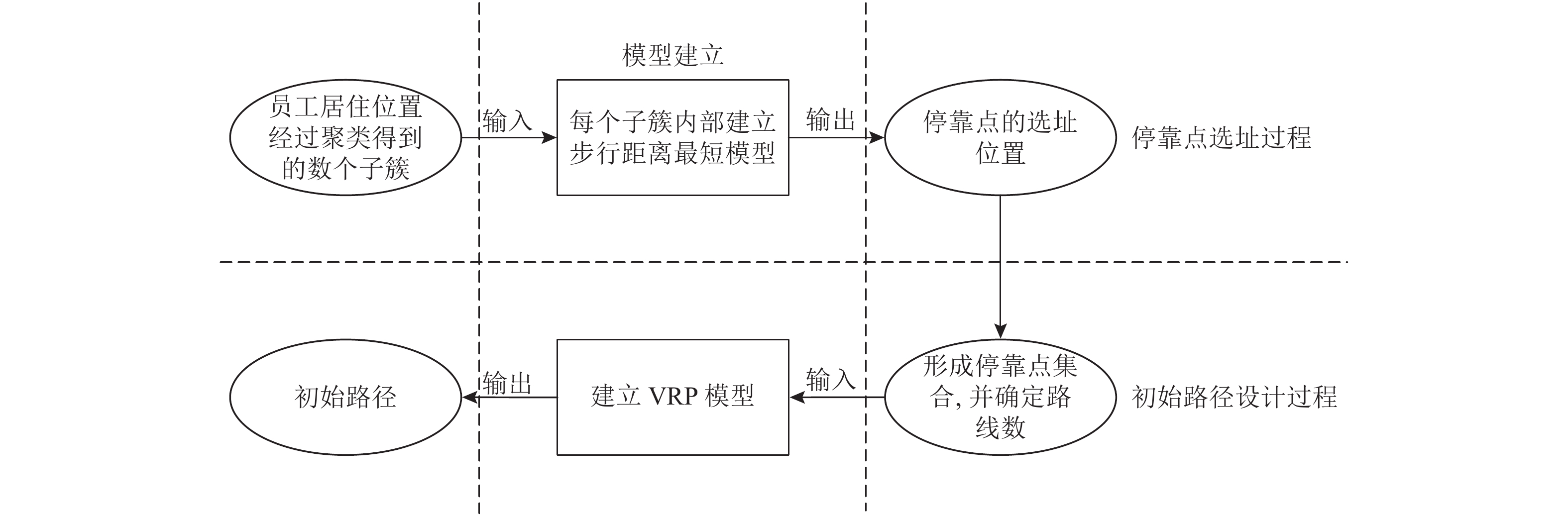
在对通勤车进行动态车辆路径优化前，需要优先考虑停靠点的选址问题，通过建立“步行距离最短模型”来解决。在解决动态车辆路径问题时，将其划分为初始路径设计和动态路线调整两个部分来实现，为初始路径设计过程建立合适的VRP模型。具体的模型和步骤如图1所示。

图  1  建立模型的步骤

Figure  1.  Model construction stages

下载: 全尺寸图片 幻灯片

2.1   符号及定义变量

Q_i为员工住址的坐标；

${Q}_{i}^{*}$ 为规格化后的员工住址坐标；

P为停靠点坐标；

O为住址到停靠点的距离和；

S为通勤车集合；

d_i为第i个停靠点的员工数量；

q为通勤车的座位数；

K为停靠点集合；

V为所有节点 (企业、停靠点)的集合；

L为集合V的真子集；

Z为通勤车的最短行驶路径；

c_ij为从i停靠点到j停靠点的最短行驶距离；

2.2   停靠点选址过程分析

停靠点的选址主要受停靠点数量和用户住址的影响，根据停靠点的服务半径要求大致确定出停靠点数量设置的范围，计算并分析多种方案下停靠点选址对初始路径设计的影响。利用聚类方法在空间上对用户住址进行划分，并建立步行距离最短模型进行求解。考虑到上下班高峰期时间段上班族对效率的高要求，停靠点的选择以最便利为原则，在建立模型之前需要确定某一处停靠点为哪片区域的上班族提供服务，即将所有参与研究的上班族居住点划分为哪些集合。利用K-means聚类方法来划分子簇，将各个住址坐标 ${Q}_{i} ({x}_{i},\;{y}_{i})$ 视作需要进行划分的元素点，以欧氏距离作为划分的相似度。在聚类前对所有住址坐标进行规划，避免由于横纵坐标范围不同对聚类属性产生的影响，规格化后的住址坐标记为 ${Q}_{i}^{*} ({x}_{i}^{*},\;{y}_{i}^{*})$ ，横坐标规格化的公式如式 (1)，纵坐标与之类似。

经过聚类分析后得到数个聚类子簇，假设第一子簇 ${R}_{1}$ 有A、B、C、D、E 5个居住区，其坐标分别为 ${Q}_{\mathrm{A}} ({x}_{\mathrm{A}},\;{y}_{\mathrm{A}}),\;{Q}_{\mathrm{B}} ({x}_{\mathrm{B}},\;{y}_{\mathrm{B}}), \cdots,\; {Q}_{\mathrm{E}} ({x}_{\mathrm{E}},\;{y}_{\mathrm{E}})$ ，按照总步行距离最短原则，设最优的停靠点坐标为P (x, y)，最短距离为O，以欧氏距离作为标准在每一个子簇内选择一个停靠点P_i。

通过数学模型得到的停靠点属于理想化的解，在实际情况中城市交通网络复杂，并不是所有的地方都能够停车，要保证选择的停靠站点在允许泊车的道路外侧，因此得到的最优解需要根据实际交通情况进行适当的修正。

2.3   初始路径设计过程分析

考虑到在上下班高峰期上班族对出行效率的高要求，将接送途中的通勤车所需数量最少、总耗时最短作为优化目标，所需最少通勤车数量，即集合S中的元素数|S|，可以通过以下公式估算。

停靠点和企业所在地点共同组成路径优化中考虑的节点集合V={P₀, P₁, P₂, $\cdots$ , P_n}，其中P₀为企业所在地点，|K|为集合K中的元素数，表示停靠点的数量。初始路径设计时不考虑其他外界因素对总行驶时间的影响，即总路程是总耗时的唯一直接影响因素，因此将目标转化为总行驶路程最短，建立VRP模型如下。

式 (3)中的括号 $\left\lfloor {\;} \right\rfloor$ 表示向下求整，旨在最大程度提高通勤车的满座率；式 (4)是目标函数，旨在求出路程最短的方案，在初始路径设计中，不会有外界因素影响通勤车行驶效率，因此可以将目标从通勤时间最短转化为通勤路径最短；式 (5)是为了保证安排的路径上车辆不会超载；式 (6)是保证每个站点的乘客都会被考虑在内；式 (7)和式 (8)是保证不会出现安排重复 (多辆车在同一站点接送)的现象；式 (9)用了DFJ方法^[25]来消除子回路，L是集合V的真子集，|L|表示集合L中的元素数，即节点的数量，对任意真子集L来说，保证节点之间的通路数量不大于节点数减一便能避免子回路；式 (10)是为了说明m_ijs和n_is是0-1决策变量。

2.4   动态调整路线分析

在动态视角下，基于实时路况信息，本文选择了关键点更新策略来对初始路径进行调整。李妍峰等^[12]设置了不同的扰动频率、标准差，将4种路线更新策略进行对比，证实了关键点更新策略的优越性。应用关键点更新策略最为重要的部分就是确定合适的“关键点”。Chen等^[11]最先提出了“critical nodes”，但却未对其进行具体说明。李妍峰等^[12]在其研究中将未抵达的客户节点和其他网络节点作为关键点。在已有的基于实时交通信息的DVRP研究中，大部分学者会为了方便求解选择采用定期更新策略、顾客处更新策略等，少数使用关键点更新策略对关键点的定义也各不相同，例如“未抵达顾客点 + 等距离间隔点”、“未抵达顾客点 + 交通慢行点”等组合。第1种组合方式即在将未抵达顾客点作为关键点的基础上，每隔一段固定距离再添加一个关键点。这种组合方式虽然可以通过调整固定间距来选择合适的关键点，但使用起来有很高的局限性，当固定间距选择过大时，会导致关键点之间距离较远，精度大大降低，与单纯的顾客点更新策略差异不大。当固定间距选择过小时，精度高，但实际交通中很多路段双向车道是分开的，如果在某个关键点接收到前方拥堵的信息时, 会因为间距过小，来不及掉头，选择其他路线。第2种组合方式即在将未抵达顾客点作为关键点的基础上，利用经验在事故、拥堵易发生点前选择某个点添入关键点。这种组合方式下调整路线难度较小，但过分强调以往经验，与拥堵发生的不确定性有一定的冲突，精度一般。

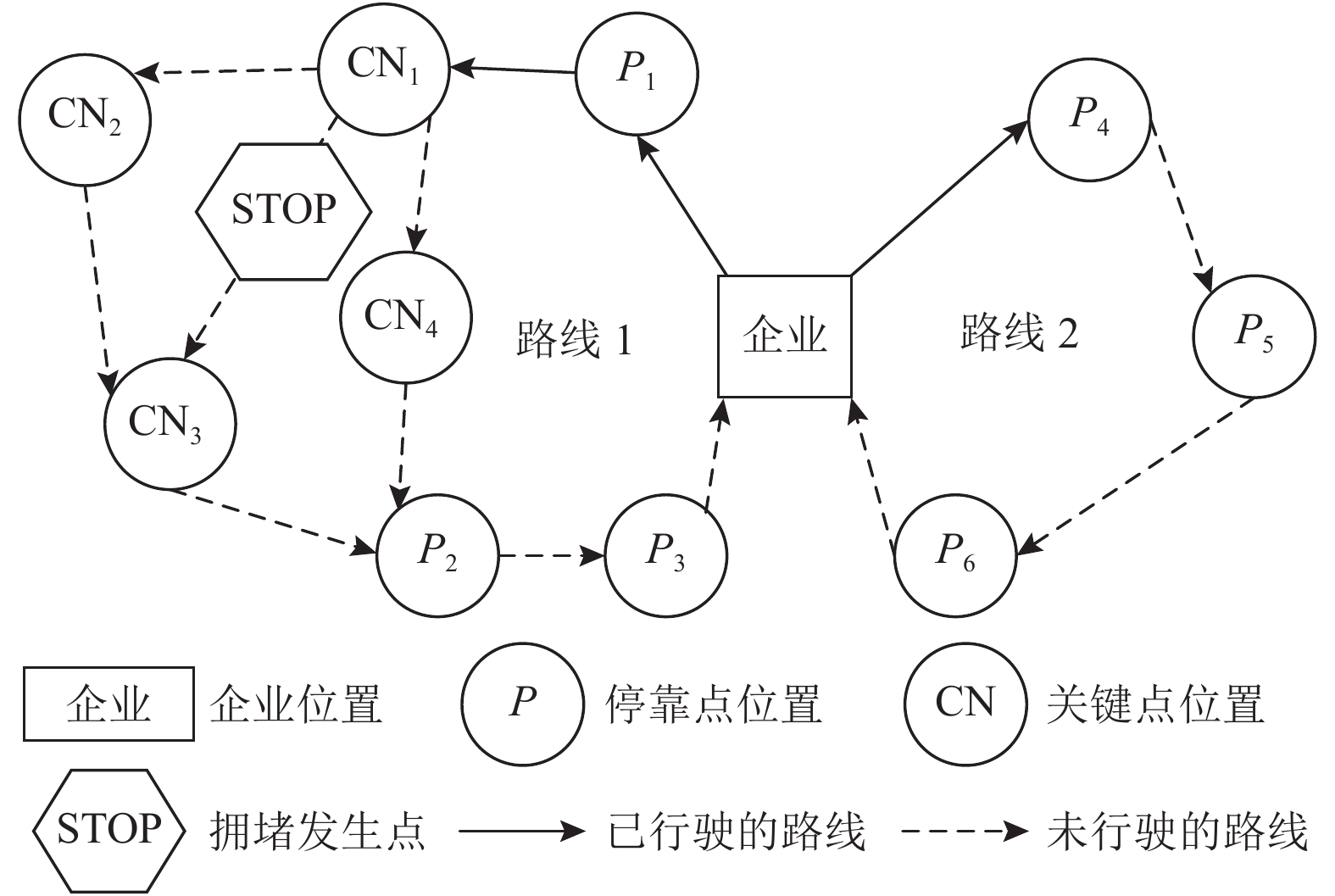
本文在这些研究基础上将关键点定义为“尚未达到的停靠点节点和路口交叉点”，即除了未到达的停靠点外，其他关键点以路口交叉点为基准进行选择，选择时需注意如下问题。1) 关键点的选择以避开初始路径中的拥堵点，且能够在抵达下一个停靠点前回到初始路径为基本要求。2) 实际交通网络中的交叉路口太多，且初始路径是在无拥堵状态下的最优路径。为了防止关键点选择过多导致出现大量偏离初始路径过远的无效备选路径，浪费计算时间，因此要求每条备选路径在回到初始路径前最多经过5个关键点。路口交叉点在交通中属于重要节点，它是车辆流向的分割点，同时分布较为均匀，将其设为关键点一方面避免了使用的局限性，另一方面也能保证调整的精度。具体路径调整方式如图2所示。其中，CN为路口交叉点前的关键点，以路线1为例，当通勤车已经经过P₁，在停靠点P₁、P₂之间找到关键点CN₁、CN₂、CN₃、CN₄以及P₂，初始路径可以表示为P₁→CN₁→CN₃→P₂→P₃，假设在关键点CN₁处收到CN₁与CN₃之间某处发生拥堵，按照初始路径行驶会大大增加行使时间，则需要比较其他关键点路径CN₁→CN₂→CN₃→P₂和CN₁→CN₄→P₂的路径耗时，从而对路径进行动态调整，在调整过程中并不会改变通勤车达到每个停靠点的顺序，避免因为交通拥堵、道路故障造成的无谓时间损耗。

图  2  动态路径调整过程示意图

Figure  2.  Dynamic adjustment of routes

下载: 全尺寸图片 幻灯片

3.   算法设计

本文的研究涉及到的问题较多，针对每个问题都需要设计相对应的算法。由于涉及到数据量较大，如何选择合适的算法使得能够快速得到结果就显得尤为重要。在求解停靠点选址问题时，本文选择最速下降法来迭代寻优；通勤车的初始路径设计不考虑外界因素影响，即传统的VRP问题，本文设计收敛性较强，收敛速度快的粒子群算法；在进行动态调整路径时，本文选择Dijkstra算法进行求解。具体的算法流程如图3所示。

图  3  求解算法流程图

Figure  3.  Algorithm flow chart

下载: 全尺寸图片 幻灯片

3.1   最速下降法

步行距离最短模型即涉及两个变量的无约束极值问题，一般采用求偏导的方式即可得到最优解，但当数据量过大无法通过计算得到答案时，求导就不再适用。最速下降法又称为梯度法，以一定的步长沿着目标函数的负梯度方向不断迭代，直到达到最低点，利用算法时需要确定初始解向量U，精度eps。在Matlab中利用最速下降法，可以迅速找出最优解。

3.2   粒子群算法

求解初始路径时采用粒子群算法，具体步骤如下。

1) 构造粒子表达式。针对每个停靠点，需要确定的问题如下。 (1)由哪辆车负责哪些停靠点员工的接送； (2)该停靠点在路径中达到的次序。通过对车辆编号以及接送次序的安排，可以直接确定所有路径。利用粒子群算法得到两个问题的解便可得到通勤车的具体行驶路径。在粒子群算法中，每个粒子群都只能代表一个解，粒子的状态通过位置向量和速度向量来表示，求解问题 (1)的粒子位置向量和速度向量为T_S和H_S；求解问题 (2)的粒子位置向量和速度向量为T_K和H_K。位置向量表示迭代过程中的可行解，速度向量表示粒子下一次迭代的运动速度大小和方向，因此可以通过迭代找到最优的粒子，其位置向量T_S、T_K反映的即为最优状态下接送某一停靠点乘客的车辆编号、该停靠点在本条路径的次序。

2) 确定粒子的初始位置与初始速度。针对本文研究的问题，一个停靠点为一个维度，对每个粒子位置向量T_S的每一维取 (1，|S|)之间的整数，T_K的每一维取 (1, | K|)之间的实数；对每个粒子速度向量H_S的每一维取 (− (|S|−1)，|S|−1)之间的整数，H_K的每一维取 (− (|K|−1)，|K|−1)，把每个粒子的初始评价值作为迭代前个体粒子的最优解。

3) 更新粒子的位置与速度。利用粒子的个体极值p_best和全局极值g_best来不断更新，根据粒子位置向量并用式 (4)算得评价值，从而比较粒子当前位置的优劣性。个体极值p_best为该粒子在之前所有迭代中的最优评价值，全局极值g_best为整个粒子群在之前所有迭代中的最优评价值。粒子的位置和速度进行更新的公式为

在第Z次迭代中，H指的是粒子的速度；w是惯性权重，一般取值在0.1 ~ 0.9之间；r₁和r₂是学习因子，有固定的取值；rand ( )是0 ~ 1之间的随机数；Present表示粒子在此次迭代中的评价值。

4) 终止策略。在当前迭代次数未超过最大次数max DT之前，如果找到全局最优粒子位置满足最小界限，可以直接以该粒子的位置向量作为最优解输出，未找到则可以继续迭代；而当前迭代次数超过最大次数max DT时，直接结束迭代，以当下全局最优粒子位置作为最优解输出。

3.3   Dijkstra算法

利用Dijkstra算法来完成动态调整路径的过程。Dijkstra算法利用广度优先搜索思想，被很多学者用来求解两点之间的最短路，被认为是求无负权网络最短路问题的最好方法，具体步骤如下。首先算出路径网络中各边的权重 (可以为长度、耗时等)，设立一个关键点集合G₁，最初集合G₁中只包含路线调整前的末尾关键点CN₁一个元素，未通过的其他关键点都在集合G₂中。从G₂中找出所有与G₁中关键点 (即CN₁)有路径连通关系的关键点CN_i (i=2, 4)，比较选出权重最小的关键点，将其加入到G₁并从G₂中剔除；再找出与G₁中关键点有路径连通关系的关键点，在G₂中选出总权重 (即从CN₁到该关键点的权重和)最小的关键点将其加入G₁并从G₂中剔除，不断迭代直至G₂为空集。关键点数量较少时可以通过标号法解决，当计算难度较大时可以在Matlab上通过编程快速求解。

4.   实证分析

在大中小城市协调发展的背景下，我国的中小城市的经济得到快速发展，交通运输的需求同时也不断增长，大城市一般拥有较为健全的轨道交通系统，有轨电车、地铁等交通方式为公路交通释放了很大一部分压力，而中小城市受限于原有城市布局，大部分交通压力都集中在公路交通上，交通拥堵现象已经逐渐开始成为中小城市的“痛点”，因此选择中小城市来研究通勤车路径会更有实际意义。在《2019年度中国城市交通报告》中，秦皇岛市高峰期城市交通拥堵同比提高10.68%，拥堵情况在同类型 (汽车保有量同一范围)的城市中排行第三，上班族面临着严重的通勤问题。考虑到通勤车主要用于职住分离较为严重的企业，本文选择秦皇岛经济技术开发区为研究对象。

秦皇岛的城市布局具有一定的特殊性，生活居住区大多集中在市中心一带的位置，而大型的工作园区却又在较为偏远的开发区位置，直达的公交路线少且耗时长。因此，大多人会选择私家车出行，而过多的私家车又容易导致交通拥堵的出现。因此，为上班族优化通勤车辆的行驶路径，不仅可以提高他们的通勤效率，还可以有效降低私家车的使用次数，减少交通拥堵情况的出现，缓解城市交通压力。通过随机调查，秦皇岛市经常发生交通拥堵的时间和地点如表1所示。

表  1  秦皇岛市拥堵情况调查

Table  1.  Survey of traffic jams in Qinhuangdao

拥堵发生的时间		拥堵发生的地点
7:30 —8:30	17:00 —18:20	秦皇西大街与海阳路交叉口
7:30 —8:30	17:00 —18:00	海阳路主线
7:30 —8:30	16:00 —17:40	秦皇西大街西段路段
7:30 —8:30	16:40 —17:40	建设大街与文化路交叉口
7:30 —8:30	17:00 —18:20	河北大街与民族路交叉口
8:00 —9:00	17:00 —18:20	河北大街汤河公园路段

下载: 导出CSV 

| 显示表格

通过对时间的分析，可以大致确定出两个拥堵频繁发生的时间段，分别是早上的7:30 —9:00和下午的16:30 —18:30。通过对拥堵路段以及交通流向的分析，选择必经拥堵路段来通勤的上班族的居住小区作为本次实证的对象。员工居住区的坐标以小区中心所在位置为准，结合实际调查结果，在地图上建立相应的坐标系，如表2所示。实证的算法求解过程均在Matlab R2018a软件上进行编程，在Win10环境下，CPU为2.70 GHz，内存为7.9 GB的计算机上完成。

表  2  研究选择的20个居住区位置坐标

Table  2.  Coordinates of the 20 selected residential districts

序号	小区名称	坐标位置	规格化		序号	小区名称	坐标位置	规格化
1	天成佳境	(0, 6.6)	(0, 0.94)		11	首府	(11.5, 2.5)	(0.63, 0.33)
2	学府嘉园	(2.2, 7.0)	(0.12, 1.0)		12	和安里小区	(12.4, 3.5)	(0.68, 0.48)
3	3区	(3.5, 6.2)	(0.19, 0.88)		13	红卫里社区	(12.7, 2.8)	(0.69, 0.37)
4	中冶果岭湾	(2.4, 5.1)	(0.13, 0.72)		14	纤维里小区	(10.8, 5.0)	(0.59, 0.70)
5	公园里	(6.8, 1.8)	(0.37, 0.22)		15	河涧里小区	(13.8, 4.7)	(0.75, 0.66)
6	泰盛家园	(7.7, 2.0)	(0.42, 0.25)		16	服务北里小区	(15.6, 1.6)	(0.85, 0.19)
7	碧景华庭	(8.3, 2.3)	(0.45, 0.30)		17	红警里小区	(17.5, 0.8)	(0.96, 0.07)
8	和平里	(9.2, 3.0)	(0.50, 0.40)		18	康乐里	(16.0, 3.0)	(0.87, 0.40)
9	建新里	(11.2, 0.3)	(0.61, 0)		19	人民里小区	(15.9, 3.9)	(0.87, 0.54)
10	迎秋西里	(13.5, 0.9)	(0.74, 0.09)		20	红桥里小区	(18.3, 3.1)	(1, 0.42)

下载: 导出CSV 

| 显示表格

参考公共交通站点的服务半径要求550 ~ 650 m，以所选取的20个小区最远直线距离 (1号与20号)为直径作出圆形覆盖面，发现大约需要4.78 ~ 5.65个停靠站才能满足服务范围覆盖的要求。为了证明停靠点选址会对路径产生影响，本文分别选择4、5、6个停靠站，通过比较初始设计路径的长度来分析3种情况在提高通勤效率上的优劣。以选取5个停靠点为例，则聚类的目标数k = 5，员工住址的坐标及规格化后的结果如表2所示。虽然初始聚类中心的选择不会影响最终聚类结果，但会对聚类过程难易产生很大影响，因此需要根据地理位置进行初步的直观判断，选择较为分散且能代表某块区域的元素点。本文选择1、8、9、12、18作为初始聚类中心，形成A、B、C、D、E 5个聚类子簇，最终只经过3次迭代后聚类结果就稳定，如表3所示。在每个聚类子簇里建立一个基于步行距离最短的数学模型，以A子簇为例，建立模型为

表  3  聚类过程中的结果

Table  3.  Results for each clustering step

聚类子簇	A	B	C	D	E
第1次聚类	1、2、3、4	5、6、7、8、11	9、10	12、13、14、15	16、17、18、19、20
第2次聚类	1、2、3、4	5、6、7、8、11	9、10	12、13、14、15、19	16、17、18、20
最终聚类	1、2、3、4	5、6、7、8、11	9、10	12、13、14、15、19	16、17、18、20

下载: 导出CSV 

| 显示表格

利用最速下降法在Matlab上进行求解。设置初始解向量U= (0 0)，即坐标为 (0,0)的点先被假设为迭代前的停靠点位置，精度eps = 1.0e⁻⁶，其中，e ≈2.718 281 83，是一个无限不循环小数。经过9次迭代，得到拟选取的停靠点坐标为P_A (2.269 4, 6.340 6)。同理，可以得到其他停靠点的坐标，分别为P_B (8.300 0, 2.300 0)，P_C (12.024 1, 0.515 0)，P_D (12.684 6, 3.615 9)，P_E (16.582 4, 2.145 8)。根据道路实际情况对停靠点的位置进行适当调整，得到最后的选择P₁ (沃尔沃)、P₂ (碧景华庭)、P₃ (万通大厦)、P₄ (学生之家)、P₅ (秦皇岛海三大厦)。本文选择的研究对象秦皇岛经济技术开发区反映在坐标上为P₀ (9.72, 5.86)，在拥堵易发生的时间段里截取8:00—8:30这一时间段，调查各聚类子簇的小区中有通勤需求的数量，经过整理后可得到如表4所示的数据。

表  4  各节点坐标及员工数量

Table  4.  Coordinates of stations and numbers of office workers

停靠点	P0	P1	P2	P3	P4	P5
坐标	(9.72, 2.56)	(2.27, 6.34)	(8.30, 2.30)	(12.02, 0.52)	(12.68, 3.62)	(16.58, 2.15)
员工数量	0	32	38	14	16	13

下载: 导出CSV 

| 显示表格

VRP模型中需要确定的定值仅有停靠点数和通勤车数量。已通过服务半径确定停靠点数量为5，利用式 (3)确定所需最小通勤车数量为3 (选择最为常见的中型客车作为通勤车，座位数为45)，在Matlab中利用粒子群算法进行迭代搜索，粒子的搜索维度反映在实际问题中即为停靠点的数量。设置搜索维度SD = 5，选择学习因子r₁= r₂=1.496 2，惯性权重w = 0.729 8，初始化粒子群数目N = 10；设置最大迭代次数max DT = 100，最终得到的全局最优解g_best = 41.133 1。按照比例进行还原可得到最短路径长度为13.71 km。两个粒子群的最优粒子位置向量如表5所示，T_S和T_K分别反映了问题 (1)、 (2)的解。T_S = (1, 2, 3, 3, 3)，结合问题 (1)，可以理解为由1号通勤车负责P₁停靠点员工的接送，2号通勤车负责P₂停靠点，3号通勤车负责P₃、P₄、P₅停靠点。T_K = (1, 1, 3, 1, 2)，结合问题 (2)，可以理解为P₁停靠点在某条路线中第1个抵达，P₂停靠点在另一条线路中第1个抵达，P₃停靠点在其他路线中第3个抵达，P₄停靠点第1个抵达，P₅停靠点第2个抵达。将两个问题得到的信息整合，可以得到3条初始路径：P₀→P₁→P₀，P₀→P₂→P₀，P₀→P₄→P₅→P₃→P₀。

表  5  求解得到的粒子位置向量

Table  5.  Obtained particle radius vectors

粒子位置向量	P1	P2	P3	P4	P5
${\boldsymbol{T}}_{_{\mathit{S}}}$	1	2	3	3	3
${\boldsymbol{T}}_{_{\mathit{K}}}$	1	1	3	1	2

下载: 导出CSV 

| 显示表格

当车辆数目越多，选择的初始化粒子群数目应该越大，从而避免得到的结果为局部最优解。在此基础上变更粒子群数目，设置N = 20、30、40分别进行求解，得到的结果与N = 10时一样，说明粒子数目为10的粒子群已经足够精确求解本文实例。另外，随着w值的增大，得到最优路径所需迭代的次数增多，但w过小容易陷入局部最优。调整惯性权重w，取w = 0.229 8、0.529 8以及0.829 8，分别计算后所得结果与原结果相近，因此可以判定结果的准确性。为了分析不同停靠点选址对通勤车路径规划产生的影响，保持学习因子r₁ = r₂ = 1.4962，惯性权重w = 0.729 8，初始化粒子群数目N = 10。设置最大迭代次数max DT = 100不变，分别求解出设立4、6个停靠站 (即聚类目标数k = 4或6，搜索维度SD = 4或6) 时初始路径设计的结果。比较结果如表6所示，随着停靠点选址数量的变化，设计的初始路径长度也有所不同。当选择4个停靠点时，实际距离最短，通勤车的行驶效率是最高的；当选择6个停靠点时，实际距离最长，通勤车的行驶效率将最低。

表  6  选取不同数量停靠点的比较分析

Table  6.  Comparative analysis for different numbers of stops

停靠点数量		停靠点服务范围所覆盖小区	停靠点设置位置坐标	通勤车初始路径设计	全局最优解 (gbest)	实际距离/km
4	P1	1、2、3、4	(2.27, 6.34)	P0→P1→P0 P0→P2→P0 P0→P3→P4→P0	36.6001	12.20
	P2	5、6、7、8、11	(8.30, 2.26)
	P3	9、10、16、17	(13.50, 0.90)
	P4	12、13、14、15、18、19、20	(13.99, 3.82)
5	P1	1、2、3、4	(2.27, 6.34)	P0→P1→P0 P0→P2→P0 P0→P4→P5→P3→P0	41.133 1	13.71
	P2	5、6、7、8、11	(8.30, 2.30)
	P3	9、10	(12.02, 0.52)
	P4	12、13、14、15、19	(12.68, 3.62)
	P5	16、17、18、20	(16.58, 2.15)
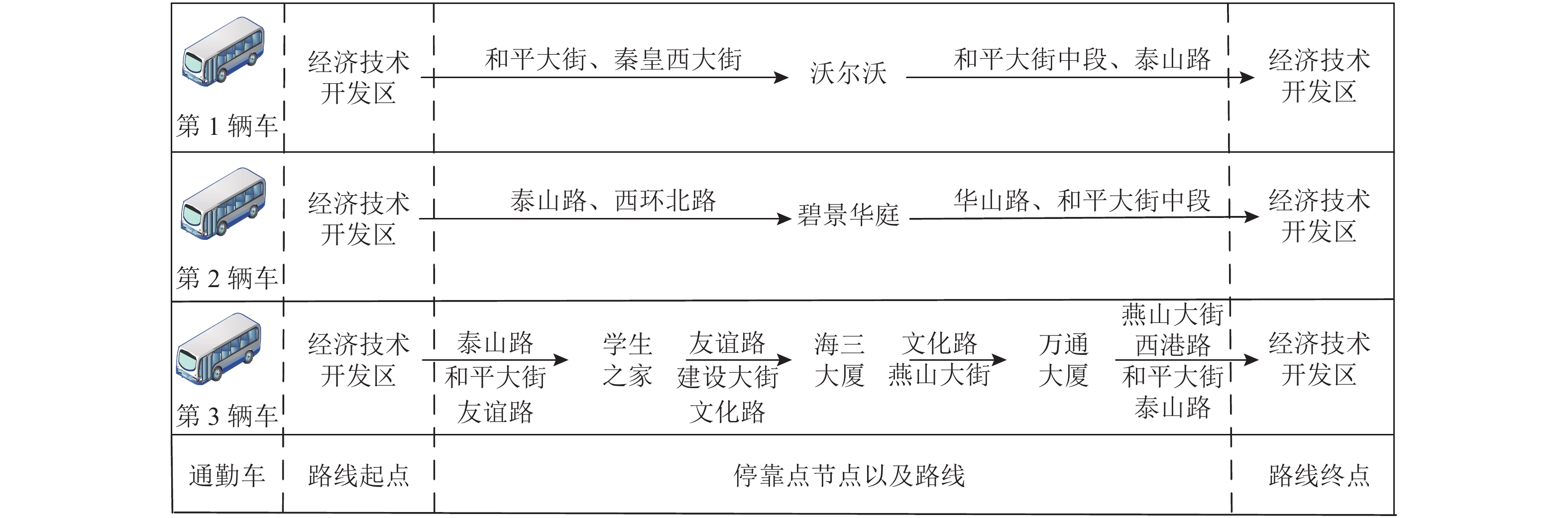
6	P1	1、2、3、4	(2.27, 6.34)	P0→P2→P1→P0 P0→P5→P0 P0→P4→P6→P3→P0	47.878 9	15.96
	P2	5、6、7、8	(8.00, 2.20)
	P3	9、10	(11.96, 0.50)
	P4	11、12、13、15	(12.44, 3.40)
	P5	14	(10.80, 5.00)
	P6	16、17、18、19、20	(16.23, 2.81)

下载: 导出CSV 

| 显示表格

由于配置4个停靠点时将略微超出公共交通站点的服务半径要求，这将导致上班族出发步行至停靠点的距离过远，会对通勤车的服务便利性造成一定的影响。因此动态路线调整过程以配置5个停靠点为例继续进行分析，将求解的3条初始路径还原为实际交通的路线，可以得到优化后的初始路线如图4所示。

图  4  秦皇岛经济技术开发区通勤初始路径设计图

Figure  4.  Design of initial routes for Qinhuangdao Economic and Technological Development Zone

下载: 全尺寸图片 幻灯片

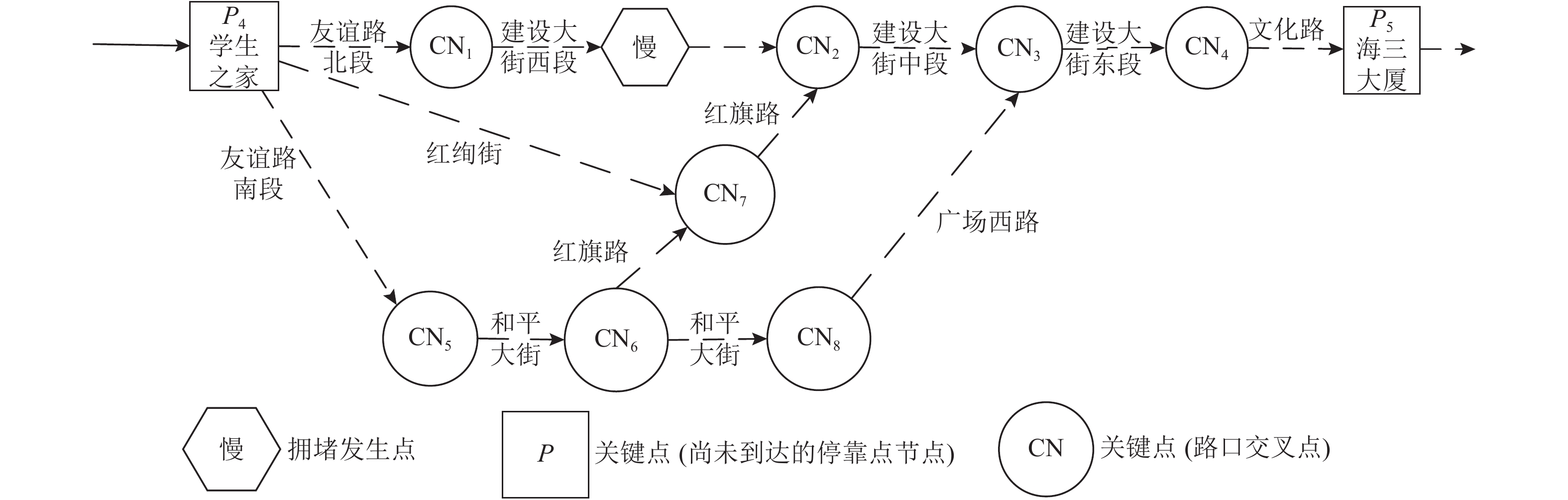
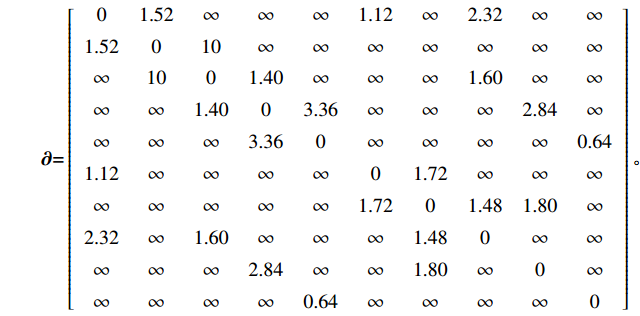
依照本文对关键点的定义和要求，在通勤车行驶前，分别为3条路径找到14、8、24个除停靠点之外的关键点，通勤车在接送上班族是优先按照初始路径行驶，每到关键点就自动接受前方实时路况信息，从而决定是否要调整路径行驶。在随机调查过程中，建设大街西段某处发生拥堵，位于停靠点P₄、P₅之间，对第3条初始路径产生了影响，使车辆行驶速度减慢。截取P₄、P₅段进行分析 ，共选取关键点10个 (包括CN₁、CN₂、 $\cdots$ 、CN₈、P₄、P₅)，如图5所示，初始路径为P₄→CN₁→CN₂→CN₃→CN₄→P₅。为了避开CN₁和CN₂之间的拥堵点对路径进行调整得到备选路径。假定通勤车在不拥堵路段的速度为15 km/h，以拥堵程度判断从CN₁行驶至CN₂需要花费10 min。将通勤车的行驶时间作为权重，在示意图上以P₄、CN₁、CN₂、 $\cdots$ 、CN₈、P₅的顺序对各个关键点排序，用矩阵∂表示路径网络中各边权重如下，矩阵的 (i，j)位置表示i号到j号的行使时间，∞表示两个关键点之间没有直接通路。在Matlab中可以得出结果为 (1, 8, 3, 4, 5, 10)，即动态路线调整结果为P₄→CN₇→CN₂→CN₃→CN₄→P₅，且总行驶时间为9.32 min，相较于拥堵状态下初始路径行使时间16.92 min，通勤效率提高大约44.92%。

图  5  交通拥堵情况下的动态路径调整

Figure  5.  Dynamic path adjustment under traffic congestion

下载: 全尺寸图片 幻灯片

在无拥堵的理想状态下，依照3条初始路径行驶花费的通勤时间分别为23.25 min、25.38 min、27.84 min，结合每条路线中包含的员工人数，可以得出人均通勤时间为25.72 min。调查得到员工当下的人均通勤时间大约为40 min，而在实际交通中如果发生拥堵，员工的通勤时间将延长到50 min左右。在本文的动态路径优化基础上，无拥堵状态下员工的通勤效率可以提高35.7%，初始路径中存在拥堵时通过动态调整路线会使行驶路径长度有所增加，但增加的行驶时间远远小于拥堵导致的等待时间，平均通勤时间也可以控制在30 min以内，通勤效率相较于优化前可以提高40%左右。

5.   结论

本文主要对基于实时交通信息的通勤车动态路径优化进行研究，借鉴“初始路径设计 + 关键点更新策略”组合形式完成优化过程，在初始路径设计时充分考虑到上班族对高效通勤的需求，建立以行驶路径最短为目标的VRP模型，采用粒子群算法求解出理想状态下的初始最优路径，在此基础上将关键点定义为“尚未达到的停靠点和路口交叉点”，利用关键点更新策略并结合Dijkstra算法实现路径的动态调整。最后进行实证分析，得到一套最优的通勤车行驶路径优化方案，并计算出通勤时间，验证模型和算法的有效性，可以在很大程度上提高上班族的通勤效率。但本文在研究初始路径优化的过程中忽视一些时间成本，例如上下车耗时成本、通勤车早到的等待时间成本、晚到的惩罚成本等，如何根据实际情况对模型进行调整，实现上班族真正意义上的通勤效率最高，将是未来研究的方向。