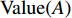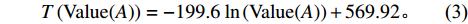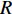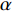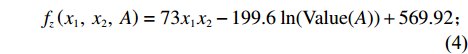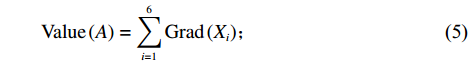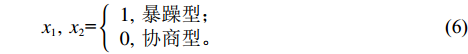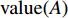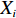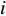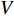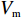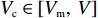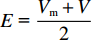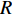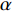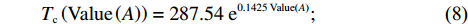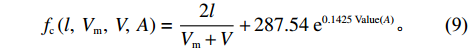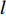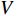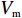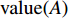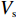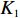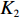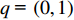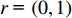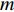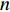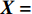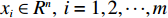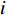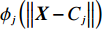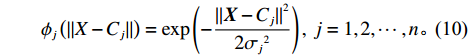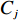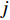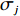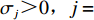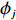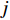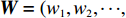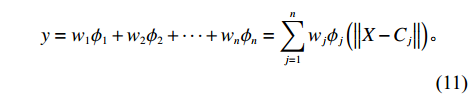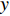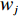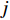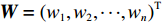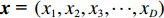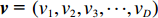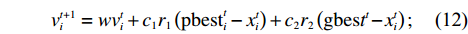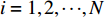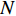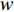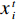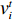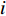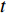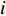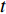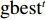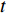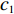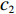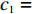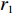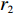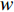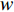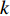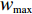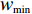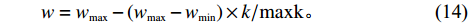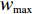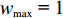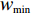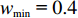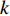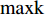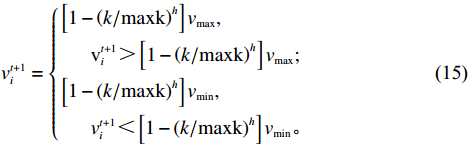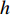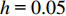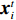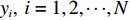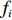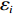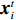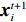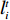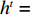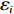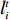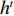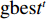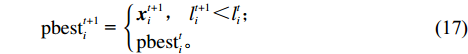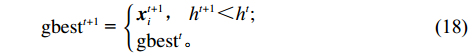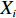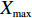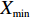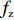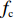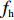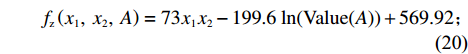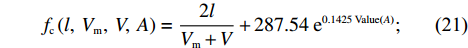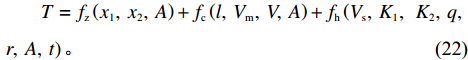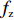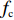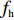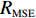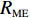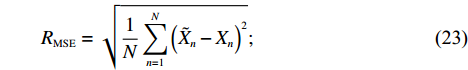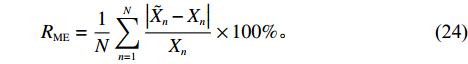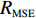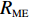A Prediction Model of Occasional Congestion Dissipation Time Based on the Whole Process
-
摘要:
为减少偶发性交通拥堵消散时间预测误差，基于事故全过程将拥堵消散时间分为驻留时间、处置时间及恢复时间，从驾驶员性格特征、事故等级特征值、初始速度建立驻留时间和处置时间回归模型，利用线性递减时变权重及速度限制改进标准粒子群算法优化RBF神经网络权重，以TransModeler仿真数据及实测数据为训练样本，建立偶发拥堵恢复时间RBF神经网络模型。仿真结果表明，模型平均绝对误差为245.3 s，其中改进PSO-RBF网络对恢复时间预测相对误差为11.2%，均方根误差为102.3，平均相对误差较单一RBF网络、标准PSO-RBF网络分别下降38.1%、23.8%。
Abstract:In order to reduce the prediction error of occasional traffic congestion dissipation time, based on the whole process of the accident, the congestion dissipation time is divided into dwell time, disposal time and recovery time, and the regression models of dwell time and disposal time are established from the driver's personality characteristics, accident grade characteristic value and initial speed. The weight of RBF neural network is optimized by using linear decreasing time-varying weight and speed limiting improved standard particle swarm optimization algorithm. The RBF neural network model of occasional congestion recovery time is established by taking Transmodeler simulation data and measured data as training samples. The simulation results show that the average absolute error of the model is 245.3 s. The relative error of improved PSO-RBF network for prediction of recovery time is 11.2%, the root mean square error is 102.3, the average relative error is 38.1% and 23.8% lower than that of single RBF network and standard PSO-RBF network respectively.
-
交通拥堵从拥堵成因上可分为常发性交通拥堵和偶发性交通拥堵。常发性交通拥堵主要由供需矛盾引发，常发性拥堵在空间上具有惯性，其具有一定的可预测性，而偶发性交通拥堵多由交通事故引发，在事故点通行能力急剧下降，引发事故点上游车辆排队和交通拥堵，偶发性拥堵随机性强，极易造成路段甚至区域严重拥堵，偶发性拥堵研究近年来逐渐成为该领域的热点研究问题。
在偶发性交通拥堵预测方面，国内外已有研究。崔德冠[1]以公交车GPS数据为基础，建立基于公交车GPS数据的城市道路偶发性拥堵检测系统。周映雪等[2]以北京市二环快速路的交通流数据为基础，建立生存分析的城市道路交通拥堵持续时间预测模型。吴义虎等[3]利用元胞自动机对城市道路偶发性拥堵交通行为进行模拟。秦韬[4]利用BP神经网络对快速路交通拥堵进行识别。李狄[5]从交通管理角度对偶发性疏散策略进行研究。Malerczyk等[6]通过速度相关随机化(VDR)模型对单个车辆自发性拥堵进行评价。 Cold-Ravnkilde等[7]对外部干预行为的交通效果进行研究。Sudatta等[8]通过深度学习模型对旧金山湾地区高速公路网络交通拥堵状态进行预测。Abeer等[9]提出一种混合时态关联规则挖掘交通拥堵预测方法，通过分类机制对拥堵规则进行分析，并建立分类器来预测交通拥挤程度。Kobayashi等[10]通过实时收集和分析交通大数据，利用分布式处理技术对交通拥堵持续时长进行预测。
上述研究成果对偶发性交通拥堵研究提供了指导，但多数研究集中于对偶发性交通拥堵进行识别及模拟，对偶发性交通拥堵持续时间研究较少，部分针对持续时间的研究考虑因素较为单一、预测时间滞后或只考虑交通恢复过程，预测效果不显著。本文选取多个影响因子，建立驻留时间和处置时间回归模型，考虑恢复时间影响因素较多，利用RBF神经网络的非线性逼近能力[11]，建立恢复时间RBF神经网络预测模型，并利用改进的粒子群算法对其权值进行优化，以仿真数据和实测数据进行训练和验证，对模型适用性进行评价。
1. 基于全过程的偶发性拥堵消散时间模型
偶发性交通拥堵从时间维度上分为事故发生、驾驶员协商、交通处置、交通恢复4个阶段，当双方驾驶员自行协商解决时，不存在交通处置阶段。对应消散时间可表征为驻留时间、处置时间、恢复时间。
偶发性交通拥堵是由随机事件引发造成交通局部通行能力降低造成上游区交通拥堵的现象，是由人、车、路、交通环境共同作用的交通事件。人是由驾驶员、乘客、交警组成的集合，驾驶员性格、交通管理者的处置时间是事件的人为影响因素；车型、车速、事故等级是车辆影响因素；道路等级、车道数是道路影响因素；天气、日期特征是交通环境影响因素。驻留时间受驾驶员性格、事故等级影响；处置时间受驾驶员性格、交警位置、速度影响；恢复时间受道路车速、天气、车道数、道路等级、日期特征、事故排队时长影响。拥堵消散时间模型为
T=f{\rm{z}}(x1,x2,A)+fc(l,Vc,A)+fh(Vs,K1,K2,q,r,A,t)。 (1) 式中，
f{\rm{z}} 为驻留时间函数；fc 为处置时间函数；fh 为恢复时间函数；x1、x2 为事故车辆双方驾驶员性格特征；l 为交警与事故点距离；Vc 为交警接收到报警信息后的到达速度；Vs、K1、K2、q、r、A、t 分别为路段起始车速、车道数、事故占用车道数、天气特征、日期特征、事故等级、事故排队时长。2. 模型参数标定
2.1 驻留时间函数参数
交通事故等级是拥堵消散事件的主要影响因素，事故等级受事故类型、事故严重程度共同影响。本文建立由事故类型、事故严重程度的事故等级度量函数。
设一次交通事故为
Ij,j=1,2,⋯,n ，设属性参数Xi,i=1,2,⋯,6 ，参数值为Grad(Xi) ，事故评分为各参数值求和，则事故等级特征值Value(Ij) 为Value(Ij)=6∑i=1Grad(Xi)。 (2) 由表1可知，
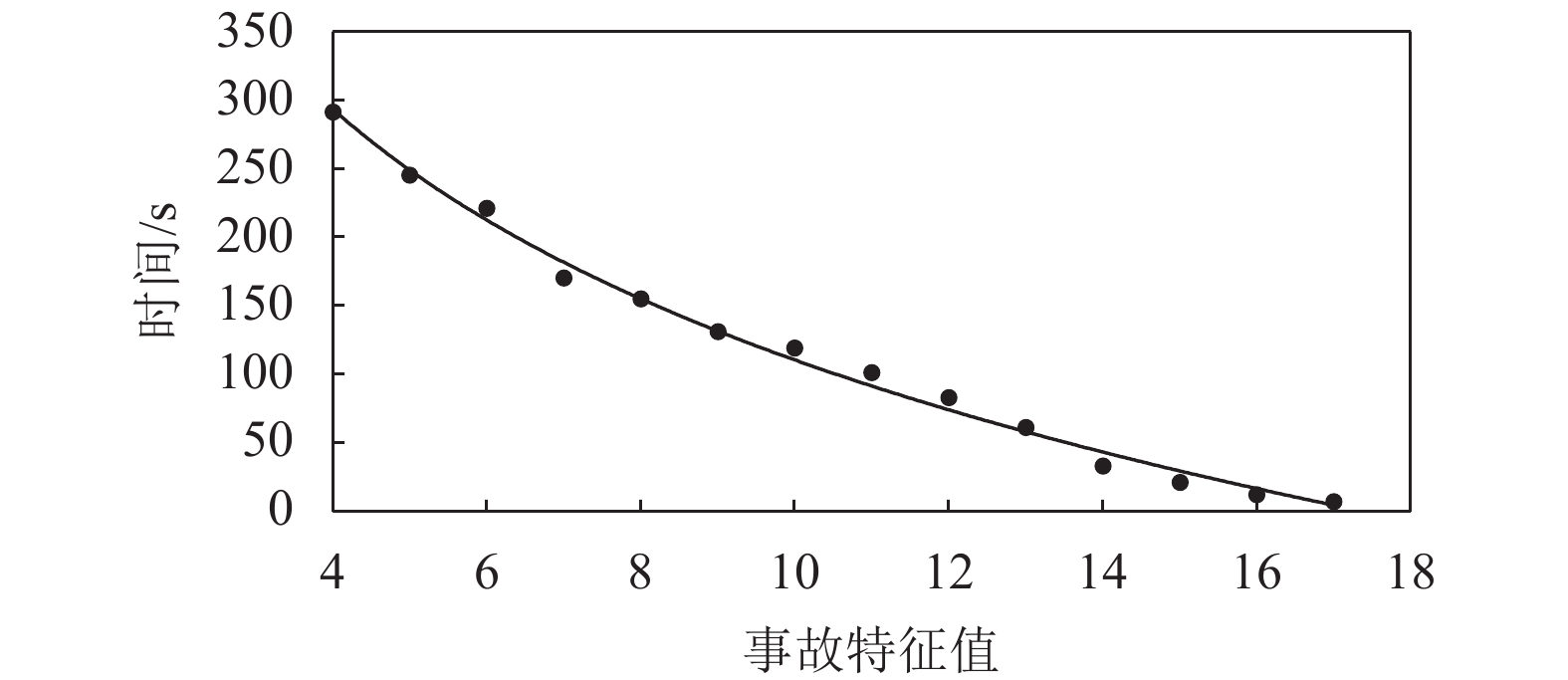
4⩽Value(Ij)⩽17 且为正整数，通过对重庆市主城区事故调查及驾驶员问卷调查，共收集256组事故等级特征值与驻留时间数据，其中重庆市公安交通管理信息网提供的数据210组，驾驶员有效问卷调查46组。为保障问卷数据代表性和典型性，驾驶员为驾驶经验3年以上、年龄25 ~ 50岁以内的成年男性或女性，问卷事故发生时间段为全天，事故发生地点为重庆市中心城区内环以内区域。对不同事故等级特征值下的驻留时间求平均，其对应关系如图1所示。表 1 交通事故等级量化表Table 1. Traffic accident rating scale序号 属性参数 参数取值 评分 1 事故类型 抛锚 1 翻车 3 火烧 3 追尾 2 碰撞 3 2 涉及车辆数 1辆 1 1-2辆 2 3及其以上 4 3 关闭车道数 1 1 2 2 3及其以上 4 4 受伤人数 1及以下 1 2 2 3及其以上 4 5 是否涉及货车 YES 1 NO 0 6 是否有危险品车辆 YES 1 NO 0 ![]()
图 1 事故等级特征值与驻留时间回归分析Figure 1. Regression analysis of the characteristic value of the accident level and the residing time由图1可知，随着事故等级特征值的增加，驾驶员驻留时间随之减少，表明事故等级对驾驶员报警倾向有显著积极影响，与现实一致。驻留时间与事故等级特征值成反比，文中建立驻留时间T与事故等级特征值
Value(A) 对数回归模型。T(Value(A))=−199.6ln(Value(A))+569.92。 (3) 利用相关系数检验法对模型进行显著性检验，模型相关系数
R =0.9967 ，通过显著性水平α = 0.01下的显著性检验。驾驶员性格也是影响因素之一，将驾驶员性格分为暴躁型、协商型两大类。经过大量问卷调查，当且仅当双方驾驶员均为暴躁型时才会加大驻留时间，且平均增加时间为73 s，则驻留时间模型可表示为fz(x1,x2,A)=73x1x2−199.6ln(Value(A))+569.92； (4) Value(A)=6∑i=1Grad(Xi)； (5) x1,x2={1,暴躁型；0,协商型。 (6) 其中，
value(A) 为事故等级特征值；Xi 为事故第i 项参数得分值。2.2 处置时间函数参数
处置时间可分为两部分，一部分是交警接到报警信息至交警出发到事故现场时间；另一部分是交警到场处理交通事故到事故车辆离开现场的处理时间。根据重庆市公安交通管理信息网提供的事故数据及问卷调查，交警根据报警后事故路段的车速情况确定交通工具，当路段车速较高时选择小汽车出警，当路段车速较低时则选择摩托车出警。设事故发生前路段平均运行速度为
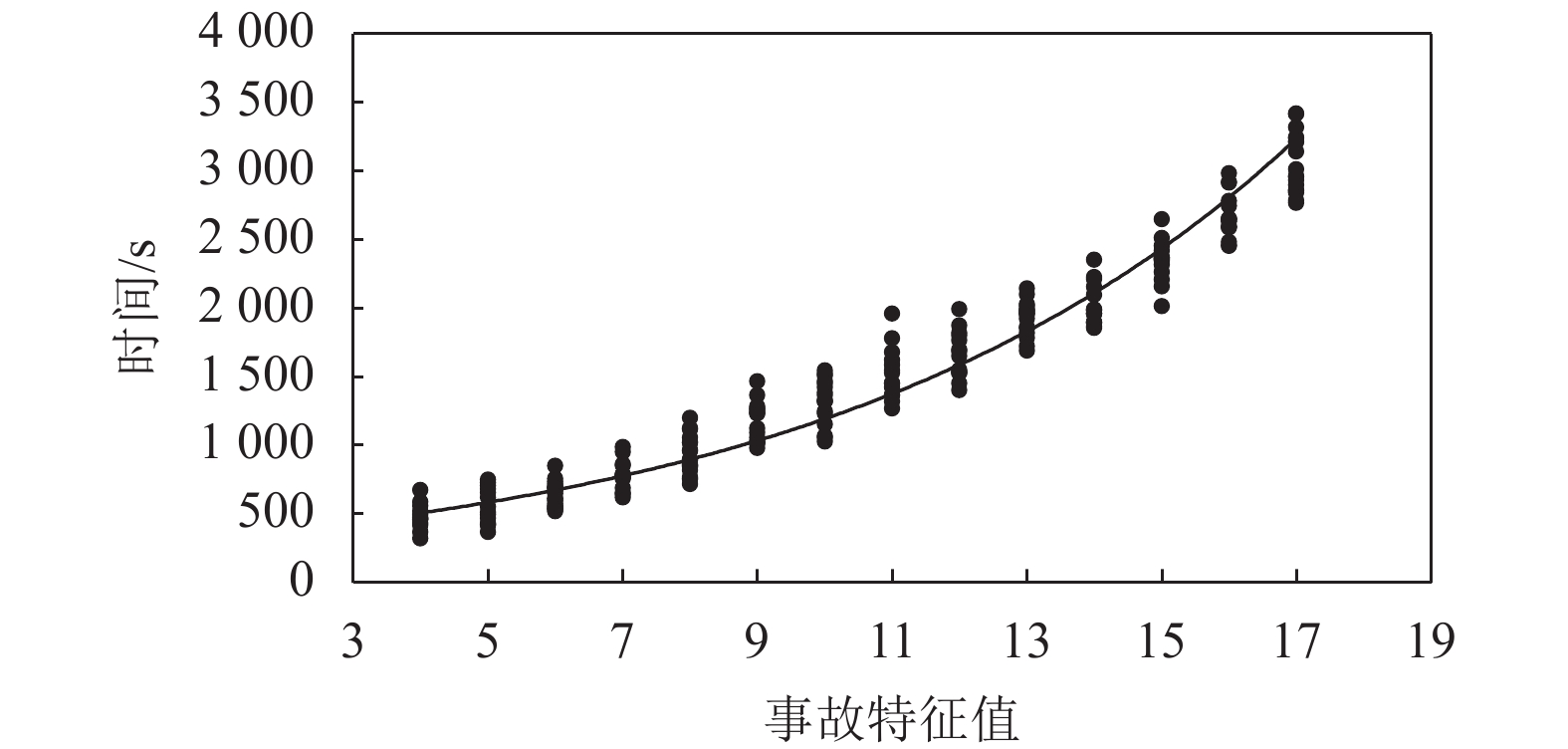
V ，摩托车平均车速为Vm ，则出警速度Vc∈[Vm,V] 。根据重庆市中心城区交警事故出警记录，小汽车出警比例为43.6%，摩托车出警比例为56.4%，两者比例几乎相等，故其期望可近似为E = Vm+V2 ，其出警时间为T=2lVm+V。 (7) 交警对事故处理时间由事故等级确定，事故等级利用事故等级特征值量化(见表1)，结合重庆市交通事故统计数据及问卷，剔除部分异常数据，共收集223组有效数据，其中重庆市公安交通管理信息网提供的数据210组，交警有效问卷调查13组，为保障问卷数据代表性和典型性，交警为工作经验3年以上、年龄25 ~ 50岁以内的成年男性或女性，问卷事故时间段为全天，事故发生地点为重庆市中心城区内环以内。随着事故特征值的增加，处置时间随之增大，建立事故特征值与处置时间回归模型见 (图2)。
![]()
图 2 事故等级特征值与处置时间回归分析Figure 2. Regression Analysis of accident grade characteristic value and disposal time当事故特征值为4时，平均处置时间为482 s，约8 min。当事故等级达到最大时，平均处置时间为
3061 s，约51 min。分别建立对数、指数、多项式回归模型并进行相关系数检验。根据检验结果，指数回归相关系数最大，R =0.9719 ，通过显著性水平α = 0.01下的显著性检验，回归模型为Tc(Value(A))=287.54e0.1425Value(A); (8) 则处置时间函数为
fc(l,Vm,V,A)=2lVm+V+287.54e0.1425Value(A)。 (9) 式中，
l 为交警到事故现场距离；V 为事故前路段平均车速；Vm 为摩托车平均速度；value(A) 为事故等级特征值。2.3 恢复时间函数参数标定
恢复时间影响因子包括路段起始车速
Vs 、车道数K1 、事故占用车道数K2 、天气特征q = (0,1) 分别表示晴天和雨天、日期特征r = (0,1) 分别表示工作日和非工作日、事故等级A 。利用具有通用逼近能力和简单拓扑结构的RBF径向基函数神经网络进行预测。RBF神经网络是具有单隐含层的三层前馈型网络。假设其有
m 个输入，n 个隐含层节点，1个输出，则输入向量{\boldsymbol{X}} = {\left( {{x_1},{x_2}, \cdot \cdot \cdot ,{x_m}} \right)^{\rm{T}}} ，{x_i} \in {R^n},\; {i = 1,2, \cdot \cdot \cdot ,m} 为第i 个输入信号，隐含层的输出{\phi _j}\left( {\left\| {{\boldsymbol{X}} - {C_j}} \right\|} \right) 为\begin{split} \qquad {\phi }_{j}\left(\Vert X-{C}_{j}\Vert \right)=\mathrm{{\rm{exp}}}\left(-\frac{{\Vert {\boldsymbol{X}}-{C}_{j}\Vert }^{2}}{2{\sigma }_{j}{}^{2}}\right),\;j=1,2,\cdots,n 。 \end{split} (10) 式中，
{C_j} 为第j 个隐含层节点的中心；{\sigma _j} 为j 个隐含层节点的基函数宽度参数，且有{\sigma }_{j} {\text{＞}} 0， j= 1,2,\cdot \cdot \cdot ,n ；{\phi _j} 为j 个隐含层节点的输出。令网络隐含层到输出层的权值为
{\boldsymbol{W}} = ( {w_1}, {w_2}, \cdot \cdot \cdot , {w_n} )^{\rm{T}} ，则网络输出层的输出为\begin{split} &\qquad y = {w_1}{\phi _1} + {w_2}{\phi _2} + \cdot \cdot \cdot + {w_n}{\phi _n} = \sum\limits_{j = 1}^n {{w_j}{\phi _j}\left( {\left\| {X - {C_j}} \right\|} \right)}。 \end{split} (11) 式中，
y 为网络输出；{w_j} 为j 个隐含层节点权重。RBF网络需求解的参数包括基函数的中心、隐含层的宽度及隐含层到输出层的连接权重。基函数的中心、隐含层的宽度目前多以K-均值聚类算法求解[12]，本文不再进行阐述。隐含层到输出层的连接权重
{\boldsymbol{W}} = {\left( {{w_1},{w_2}, \cdot \cdot \cdot ,{w_n}} \right)^{\rm{T}}} 利用粒子群优化算法(particle swarm optimization，PSO)进行求解。每个粒子根据其所处位置及周围粒子的搜索轨迹调整自身位置[13]，其整个搜索过程可以用2个矢量表示：
D 维位置矢量{\boldsymbol{x}}{\text{ = }}\left( {{x_1},{x_2},{x_3}, \cdot \cdot \cdot ,{x_D}} \right) ；D 维速度矢量{\boldsymbol{v}}{\text{ = }}\left( {{v_1},{v_2},{v_3}, \cdot \cdot \cdot ,{v_D}} \right) ，其位置迭代方程为\begin{array}{l} \qquad v_i^{t + 1} = wv_i^t + {c_1}{r_1}\left( {{\rm{pbest}}_i^t - x_i^t} \right) + {c_2}{r_2}\left( {{\rm{gbes}}{t^t} - x_i^t} \right); \end{array} (12) \begin{array}{l} \qquad x\,_i^{t + 1} = x_i^t + v_i^{t + 1}。 \end{array} (13) 式中，
i = 1,2, \cdot \cdot \cdot ,N (N 为粒子总量)；w 为惯性权重；x\,_i^t 及v_i^t 表示粒子i 在t 代的当前位置及速度向量；{\rm{pbest}}_i^t 为粒子i 在t 代的个体最优；{\rm{gbes}}{{\rm{t}}^t} 为粒子群在t 代的全局最优；{c_1} 为认知权重，{c_2} 为社会权重，取{c_1} = {c_2} = 1.7 ；{r_1} 及{r_2} 为D 维矢量参数且分布于[0,1]。标准PSO算法在处理高纬度问题时，容易早熟收敛[14]，即粒子在未到达全局最优时停滞不前[15]，陷入局部最优值，因此，对本文从惯性权重、速度限制两方面对PSO算法早熟收敛进行改进。
理想状态是在初期保持较大的探索能力，在后期保持较小的开发能力。对于固定值
w ，在迭代过程中保持不变，其适应性不足。因此提出一种线性递减时变权重。与标准算法相比，时变权重w 是迭代次数k 的函数，从{w_{\max }} 递减至{w_{\min }} ，其表达式为\begin{split} &\qquad w = {w_{\max }} - \left( {{w_{\max }} - {w_{\min }}} \right) \times k/{\rm{maxk}} 。 \end{split} (14) 式中，
{w_{\max }} 为最大值，取{w_{\max }}{\text{ = }}1 ；{w_{\min }} 为最小值，取{w_{\min }}{\text{ = }}0.4 ；k 为当前迭代次数；{\rm{maxk}} 为最大迭代次数。PSO算法在调整位置时速度呈随机分布，为避免粒子在移动时速度过大造成发散和速度过小造成停滞，通过速度限制调整搜索步长[16]，初期为跳出局部最优，应以较大步长进行搜索，后期应减小搜索步长。本文通过对速度进行动态限制，实现上述效果，其表达式为
v_i^{t + 1} = \left\{ \begin{aligned} & \left[ {1 - {{\left( {k/{\rm{maxk}}} \right)}^h}} \right] {v_{\max }},\\ &\;\;\;\;\;\; {\text{ v}}_i^{t + 1} {\text{＞}} \left[ {1 - {{\left( {k/{\rm{maxk}}} \right)}^h}} \right] {v_{\max }}; \\ &\left[ {1 - {{\left( {k/{\rm{maxk}}} \right)}^h}} \right] {v_{\min }},\\ &\;\;\;\;\;\; {\text{ }}v_i^{t + 1} {\text{＜}} \left[ {1 - {{\left( {k/{\rm{maxk}}} \right)}^h}} \right] {v_{\min }}。 \\ \end{aligned} \right.{\text{ }} (15) 式中，
{v_{\max }}{\text{ }} 为最大速度；{v_{\min }}{\text{ }} 为最小速度；h 为参数，取h{\text{ = }}0.05 。PSO算法优化RBF网络权值的核心是将粒子群中每个粒子的位置向量
{\boldsymbol{x}}_i^t 作为网络隐含层到输出层的权值，以输出值{y_i},\; {i = 1,2, \cdot \cdot \cdot ,N} 与期望值{f_i} 的误差作为粒子适应度，粒子适应度{\varepsilon _i} 为\begin{split} &\qquad {\varepsilon _i} = \frac{1}{N}\sum\limits_{i = 1}^N {{{\left( {{y_i} - {f_i}} \right)}^2}} 。 \end{split} (16) 网络隐含层至输出层的权值计算过程如下。
步骤1 初始化粒子群中的每个粒子，随机初始化粒子位置
{\boldsymbol{x}}_i^t 。步骤2 粒子位置的迭代更新，根据式(13)对粒子位置进行动态更新，更新后的粒子位置为
{\boldsymbol{x}}_i^{t + 1} 。步骤3 更新粒子的个体极值
l_i^t 和全局极值{h^t} = \min l_i^t ，当粒子的适应度{\varepsilon _i} 小于个体极值l_i^t 时，更新个体极值。当个体极值的最小值小于全局极值{h^t} 时，更新全局极值。粒子的个体最优位置{\rm{pbest}}_i^t 和全局最优位置{\rm{gbes}}{t^t} 更新过程为\begin{split} &\qquad {\rm{pbest}}_i^{t + 1}{\text{ = }}\left\{ \begin{gathered} {\boldsymbol{x}}_i^{t + 1}，{\text{ }}l_i^{t + 1} {\text{＜}} l_i^t ； \\ {\rm{pbest}}_i^t 。 \\ \end{gathered} \right. \end{split} (17) \begin{split} &\qquad {\rm{gbes}}{{\rm{t}}^{t + 1}}{\text{ = }}\left\{ \begin{gathered} {\boldsymbol{x}}_i^{t + 1}，{\text{ }}{h^{t + 1}}＜{h^t}; \\ {\rm{gbes}}{{\rm{t}}^t}。 \\ \end{gathered} \right. \end{split} (18) 重复步骤2，直到满足算法结束条件。如粒子适应度小于设置阈值或算法迭代次数达到最大值，将粒子群的最优位置作为RBF网络的权值。
3. 实例分析
3.1 基于TransModeler的数据提取方法
样本训练数量对RBF网络预测精度有直接影响。影响恢复时间的因素较多，交通事故数据收集难度较大，样本数量不足严重影响模型校核与预测。基于此，本文利用宏观专业交通仿真软件TransModeler模拟事故交通恢复过程，以仿真数据作为网络训练样本。依托重庆市城市研究中心的道路运行监测系统数据，建立渝中区中观仿真模型 (见图3)，共划分269个交通小区，涵盖渝中区快主次支路网，根据居民调查数据和RFID数据建立渝中区交通需求OD矩阵。根据OD矩阵进行路网分配后的流量作为仿真节点OD。
![]()
图 3 渝中区中观仿真示意图Figure 3. Schematic diagram of intermediate perspective simulation in Yuzhong District通过设置故障车模拟事故发生，以取消故障车模拟交通恢复初始，对路段车速进行实时数据收集，以现实事故数据与仿真数据作为样本训练检验数据，共收集30个事故点450组数据，其中现实数据8个事故点，8组数据，其余为仿真数据。
3.2 输入输出参数选择
将4组实际数据及356组仿真数据作为样本训练数据，将剩余4组实际数据及86组仿真数据作为模型网络验证数据。在训练前需进行归一化处理，归一化转换公式为
\begin{split} \qquad {X'_i} = \frac{{{X_i} - {X_{\min }}}}{{{X_{\max }} - {X_{\min }}}}。 \end{split} (19) 式中，
{X_i} 为第i 类参数值；{X_{\max }} 、{X_{\min }} 分别为该类参数的最大值和最小值。3.3 模型误差精度分析
分别建立驻留时间
{f_{\textit{{\rm{z}}}}} 、处置时间{f_{\rm{c}}} 、恢复时间{f_{\rm{h}}} 模型，则其拥堵消散时间模型为\begin{split} &\qquad {f}_{{\textit{{\rm{z}}}}}\left({x}_{1},\; {x}_{2},\; A\right)=73{x}_{1}{x}_{2}- 199.6\;\mathrm{ln}({\rm{Value}}(A))+569.92 ； \end{split} (20) \begin{split} &\qquad {f}_{{\rm{c}}}\left(l,\;{V}_{{\rm{m}}},\;V,\;A\right)=\frac{2l}{{V}_{{\rm{m}}}+V}+287.54\;{{\rm{e}}}^{0.1425\;{\rm{Value}}\left(A\right)}; \end{split} (21) \begin{split} &\qquad T={f}_{{\textit{{\rm{z}}}}}\left({x}_{1},\; {x}_{2},\; A\right)+{f}_{{\rm{c}}}\left(l,\; {V}_{{\rm{m}}},\; V,\; A\right)+{f}_{{\rm{h}}}\left({V}_{{\rm{s}}},\; {K}_{1},\; \right.{K}_{2},\; q,\; \\ &\left.r,\; A,\; t\right)。 \end{split} (22) 由于驻留时间
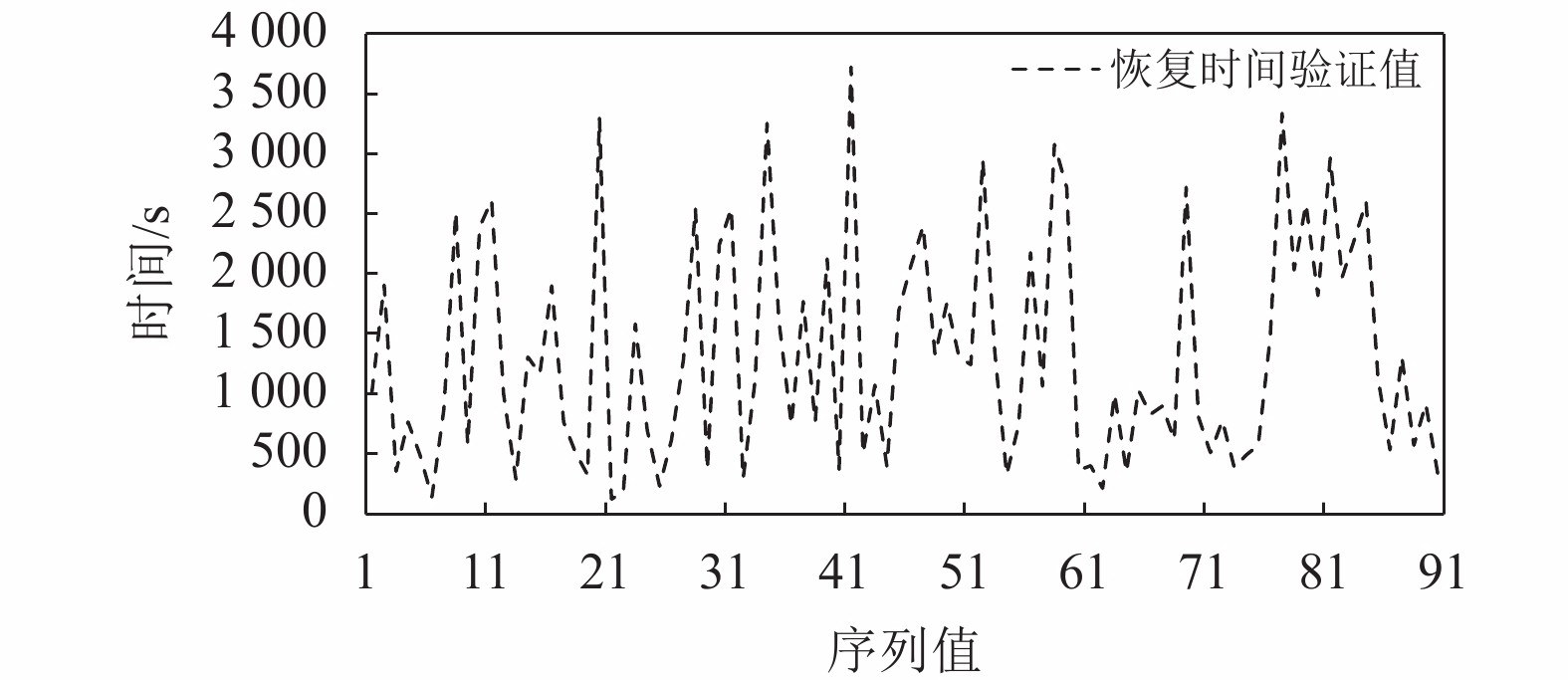
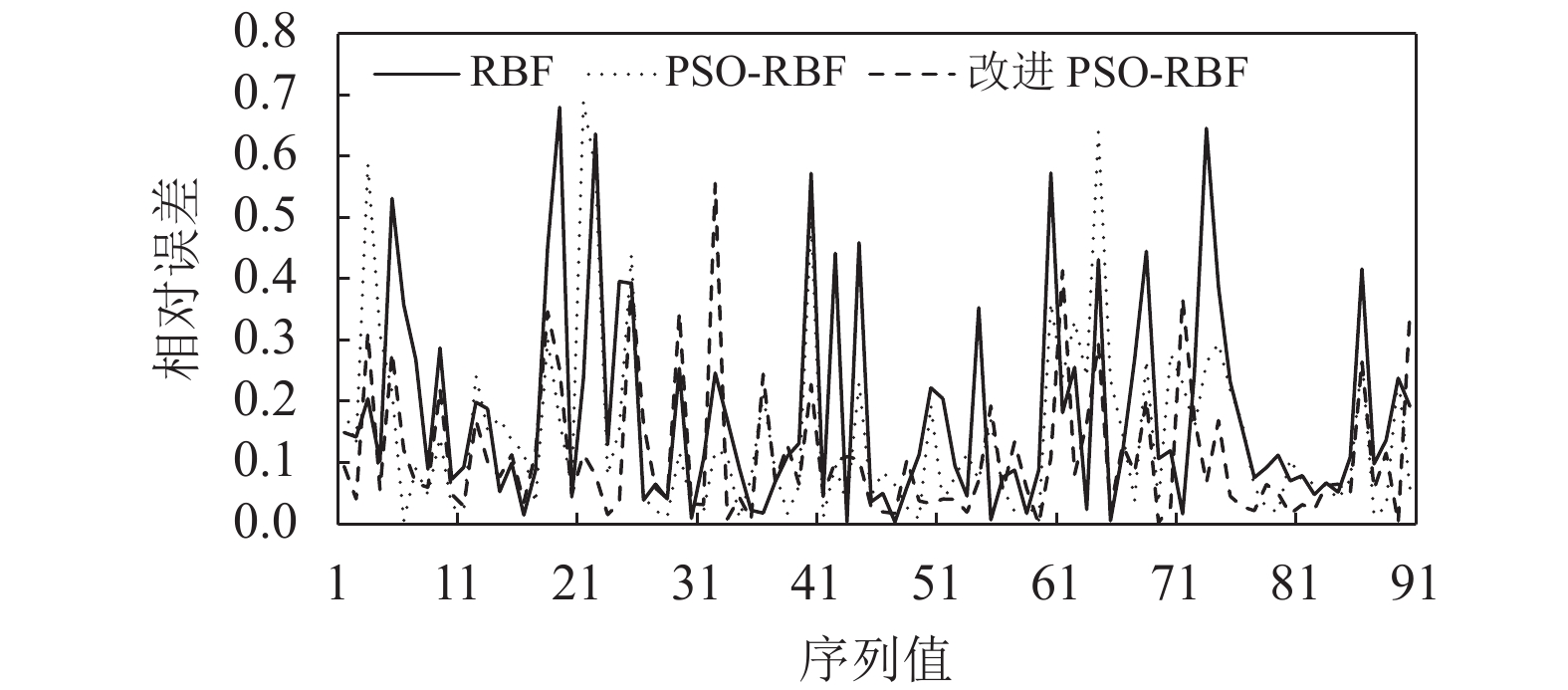
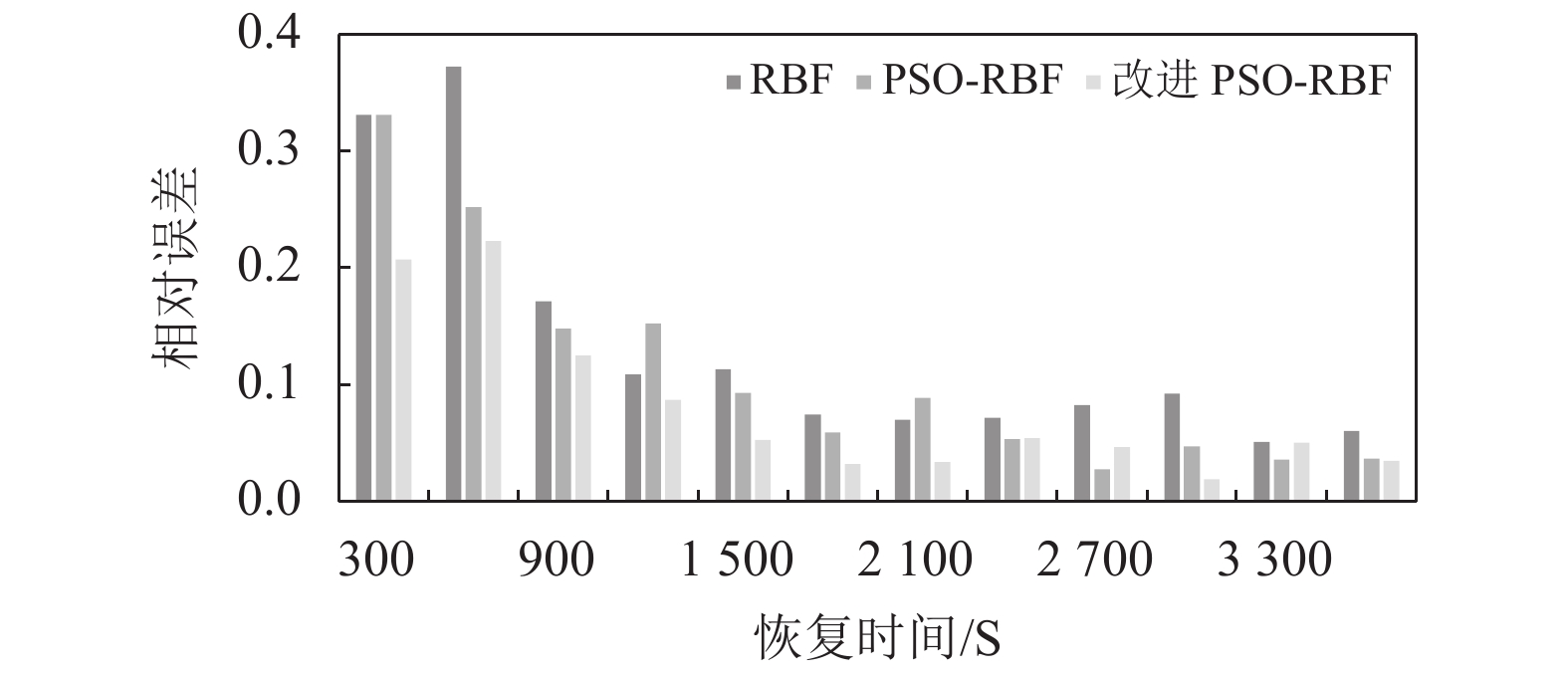
{f_{\textit{{\rm{z}}}}} 、处置时间{f_{\rm{c}}} 均通过相关系数检验，因此，下面主要对恢复时间{f_{\rm{h}}} 进行误差精度分析。利用改进PSO-RBF模型对恢复时间进行预测，测试误差采用均方根误差{R_{{\rm{MSE}}}} 、平均相对误差{R_{{\rm{ME}}}} 。\begin{split} &\qquad {R_{{\rm{MSE}}}} = \sqrt {\frac{1}{N}\sum\limits_{n = 1}^N {{{\left( {{{\tilde X}_n} - {X_n}} \right)}^2}} }; \end{split} (23) \begin{split} &\qquad {R_{{\rm{ME}}}} = \frac{1}{N}\sum\limits_{n = 1}^N {\frac{{\left| {{{\tilde X}_n} - {X_n}} \right|}}{{{X_n}}}} \times 100\% 。 \end{split} (24) 仿真及实测恢复时间验证值如图4所示，其中序列12、37、41、77为实测数据。验证样本最小恢复时间为121 s，该数据为仿真数据；最大恢复时间为
3726 s，该数据为实测数据；样本均值为1315 s。本文分别对RBF、PSO-RBF、改进PSO-RBF模型预测精度进行对比分析。根据图5、6的模型误差分布可以看出，3类模型在恢复时间0 ~ 300 s、300 ~ 600 s时平均相对误差较大。恢复时间大于900 s后，模型预测相对误差呈平稳趋势。根据表2可知，改进PSO-RBF模型的均方根误差
{R_{{\rm{MSE}}}} 及平均相对误差{R_{{\rm{ME}}}} 均比其余两类模型小，表明改进PSO-RBF模型对交通事故恢复时间具有良好的预测效果和精度。表 2 恢复时间模型误差汇总Table 2. Recovery time model error summary类型 {R_{ {\rm{MSE} } } }/{\rm{s}} {R_{{\rm{ME}}}} /\% RBF 169.6 18.1 PSO-RBF 135.5 14.7 改进PSO-RBF 102.3 11.2 偶发性拥堵消散时间模型预测误差分为驻留时间误差、处置时间误差及恢复时间误差等3类误差，由于3类时间样本数量存在差异，故本文以3类平均绝对误差和作为偶发性拥堵消散时间模型预测总误差。根据表3可知，基于全过程的偶发性拥堵消散时间模型预测平均绝对误差为245.3 s，其中驻留时间平均绝对误差16.5 s，处置时间平均绝对误差140.2 s，恢复时间平均绝对误差88.6 s。
表 3 预测模型误差汇总Table 3. Summary of prediction model errors误差 {R_{ {\rm{MAE} } } }/s 驻留时间平均绝对误差 16.5 处置时间平均绝对误差 140.2 恢复时间平均绝对误差 88.6 模型总误差 245.3 4. 结论
本文基于偶发性交通拥堵全过程，将偶发性拥堵消散时间分为驻留时间、处置时间、恢复时间函数，利用重庆市主城区交通事故数据，建立驻留时间和处置时间函数模型，以TransModeler仿真数据及实测数据，建立RBF神经网络模型，通过线性递减时变权重及速度限制对粒子群算法进行改进，利用改进PSO算法优化RBF网络权重。模型平均绝对误差为245.3 s，其中改进PSO-RBF网络对恢复时间预测相对误差为11.2%，均方根误差为102.3，表明模型对偶发性拥堵消散时间具有较高的预测精度，可服务于城市交通管理部门道路运行监测及事故交通管制，提升城市交通精细化管控水平。
-
![]()
图 1 事故等级特征值与驻留时间回归分析
Figure 1. Regression analysis of the characteristic value of the accident level and the residing time
![]()
图 2 事故等级特征值与处置时间回归分析
Figure 2. Regression Analysis of accident grade characteristic value and disposal time
![]()
图 3 渝中区中观仿真示意图
Figure 3. Schematic diagram of intermediate perspective simulation in Yuzhong District
表 1 交通事故等级量化表
Table 1 Traffic accident rating scale
序号 属性参数 参数取值 评分 1 事故类型 抛锚 1 翻车 3 火烧 3 追尾 2 碰撞 3 2 涉及车辆数 1辆 1 1-2辆 2 3及其以上 4 3 关闭车道数 1 1 2 2 3及其以上 4 4 受伤人数 1及以下 1 2 2 3及其以上 4 5 是否涉及货车 YES 1 NO 0 6 是否有危险品车辆 YES 1 NO 0 
下载: 导出CSV
表 2 恢复时间模型误差汇总
Table 2 Recovery time model error summary
类型 {R_{ {\rm{MSE} } } }/{\rm{s}} {R_{{\rm{ME}}}} /\% RBF 169.6 18.1 PSO-RBF 135.5 14.7 改进PSO-RBF 102.3 11.2
下载: 导出CSV
表 3 预测模型误差汇总
Table 3 Summary of prediction model errors
误差 {R_{ {\rm{MAE} } } }/s 驻留时间平均绝对误差 16.5 处置时间平均绝对误差 140.2 恢复时间平均绝对误差 88.6 模型总误差 245.3
下载: 导出CSV
-
[1] 崔德冠. 基于公交车GPS数据的城市道路偶发性拥堵检测与系统实现[D]. 重庆: 重庆大学, 2015. CUI Deguan. The detection and system implementation of urban road contingency jam based on bus GPS data [D]. Chongqing: Chongqing University, 2015.
[2] 周映雪, 杨小宝, 环梅, 等. 基于生存分析的城市道路交通拥堵持续时间研究[J]. 应用数学和力学, 2013, 34(1): 98-106. ZHOU Yingxue, YANG Xiaobao, HUAN Mei, et al. Survival analysis approach for estimating urban traffic congestion duration[J]. Applied Mathematics and Mechanics, 2013, 34(1): 98-106.
[3] 吴义虎, 李意芬, 喻伟, 等. 基于元胞自动机的城市道路偶发性拥堵交通行为模拟[J]. 交通科学与工程, 2014, 30(2): 72-78. DOI: 10.3969/j.issn.1674-599X.2014.02.013 WU Yihu, LI Yifen, YU Wei, et al. A simulation of the traffic behavior of the propagation of urban coincidental traffic jams based on the cellular automata model[J]. Traffic Science and Engineering, 2014, 30(2): 72-78. DOI: 10.3969/j.issn.1674-599X.2014.02.013
[4] 秦韬. 城市道路偶发性局部拥堵快速识别办法研究[D]. 长沙: 长沙理工大学, 2014. QIN Tao. Research on quickly recognition ways of the urban road non-recurrent local congestion [D]. Changsha: Changsha University of Technology, 2014.
[5] 李狄. 城市偶发性局部拥堵协调控制策略研究[D]. 长沙: 长沙理工大学, 2014. LI di. Research of coordinated control strategy on city traffic occasional congestion [D]. Changsha: Changsha University of Technology, 2014.
[6] MALERCZYK J, LERCH S, TIBKEN B, et al. Impact of intelligent agents on the avoidance of spontaneous traffic jams on two-lane motorways[J]. MATEC Web of Conferences, 2020, 308(9): 05003.
[7] COLD-RAVNKILDE S M, JACOBSEN K L. Disentangling the security traffic jam in the Sahel: constitutive effects of contemporary interventionism[J]. International Affairs, 2020, 96(4): 855-874. DOI: 10.1093/ia/iiaa093
[8] SUDATTA M, ALEXEY P, MICHAEL C. Region-wide congestion prediction and control using deep learning[J]. Transportation Research, 2020, 116(7): 102624.1-102624.21.
[9] ABEER A H, ZIAD A, TIMOTHY M, et al. Novel Congestion-estimation and routability-prediction methods based on machine learning for modern FPGAs[J]. ACM Transactions On Reconfigurable Technology and Systems, 2019, 3(12): 16.1-16.25.
[10] KOBAYASHI H, KITANO T, OKAMOTO M, et al. MAGONIA (DPB: distributed processing base) applied to a traffic congestion prediction and signal control system[J]. NTT Technical Review, 2016, 14(10): 1-4.
[11] 管硕. 基于SVM和K-均值聚类的RBF神经网络短时交通流预测[D]. 青岛: 青岛大学, 2015. GUAN Shuo. Short term traffic flow prediction of RBF neural network based on SVM and K-means clustering [D]. Qingdao: Qingdao University, 2015.
[12] 章国勇, 伍永刚, 顾巍. 基于精英学习的量子行为粒子群算法[J]. 控制与决策, 2013, 28(9): 1341-1348. ZHANG Guoyong, WU Yonggang, GU Wei. Quantum-behaved particle swarm optimization algorithm based on elitist learning[J]. Control and Decision, 2013, 28(9): 1341-1348.
[13] 朱震曙, 薄煜明, 吴盘龙, 等. Short-term power load forecasting model based on QPSO-RBFNN[J]. 南京理工大学学报, 2016, 40(1): 97-101. ZHU Zhenshu, BO Yuming, WU Panlong, et al. Short term power load forecasting model based on QPSO-RBFNN[J]. Journal of Nanjing University of Science and Technology, 2016, 40(1): 97-101.
[14] LIU J, Sun J, XU W B. Improving quantum-behaved particle swarm optimization by simulated annealing[J]. Computational Intelligence and Bioinformatics, 2006, 4115: 130-136.
[15] CHEN D B, WANG J T. An improved group search optimizer with operation of quantum-behaved swarm and its application[J]. Applied Soft Computing, 2012, 12(2): 712-725. DOI: 10.1016/j.asoc.2011.10.021
[16] SUN J, FANG W, PALADE V, et al. Quantum-behaved particle swarm optimization with Gaussian distributed local attractor point[J]. Applied Mathematics and Computation, 2011, 218(7): 3763-3775. DOI: 10.1016/j.amc.2011.09.021
-
期刊类型引用(5)
1. 徐瓅. “投资人+EPCO”模式下全过程造价控制策略研究. 建筑经济. 2025(01): 30-36 . 
百度学术
2. 张萌，孙璐璐，苏兵，王能民. 考虑空载损失的非集中式共同配送订单分派及路径优化研究. 工业工程. 2024(02): 107-118+137 . 本站查看
3. 周安峻，徐越. 全过程造价咨询服务质量影响因素研究——基于AHP-DEMATEL. 建筑经济. 2024(09): 69-77 . 百度学术
4. 任山山，买欣蕾. 基于时间序列模型的城市交通拥堵情况预测方法. 信息与电脑(理论版). 2023(10): 1-3 . 百度学术
5. 耿慧萍，董晓，冯霄，霍小平，刘加平. 城市中小学“通学型”潮汐式拥堵机理剖析. 城市发展研究. 2023(08): 32-37 . 百度学术
其他类型引用(1)
计量
- 文章访问数: 1136
- HTML全文浏览量: 37
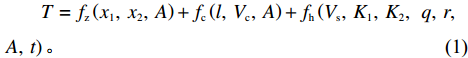
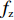
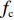
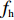
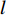
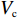
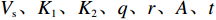
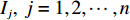
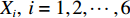
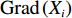
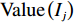
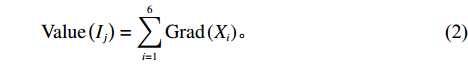
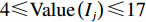
- PDF下载量: 4194
- 被引次数: 6
