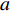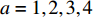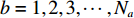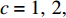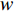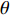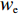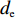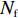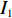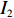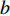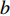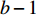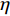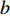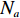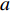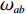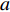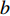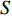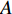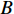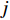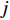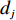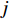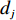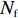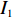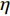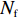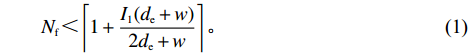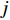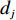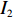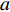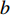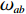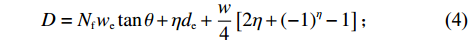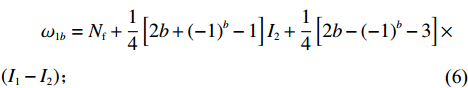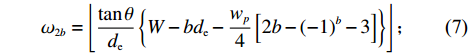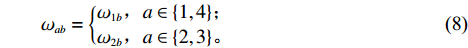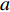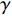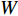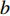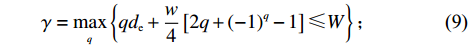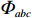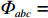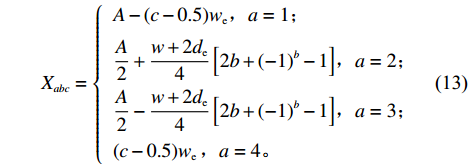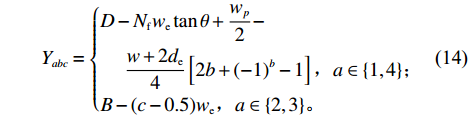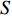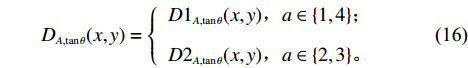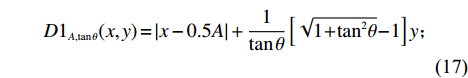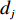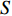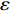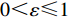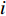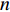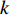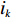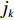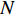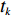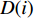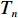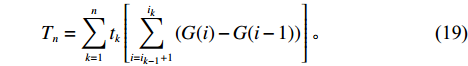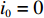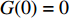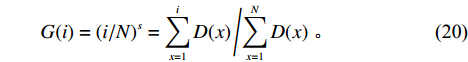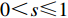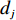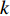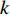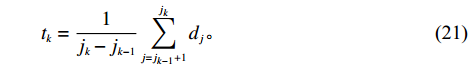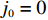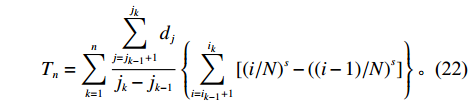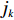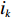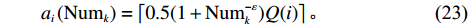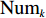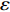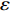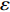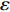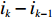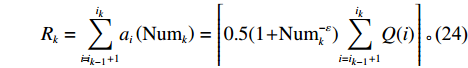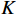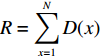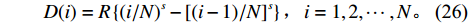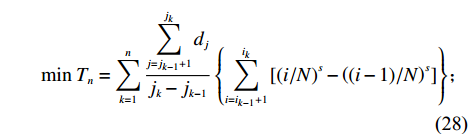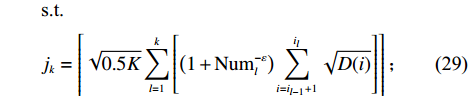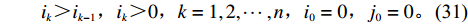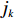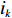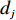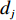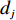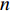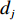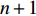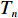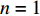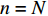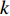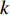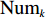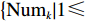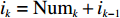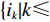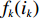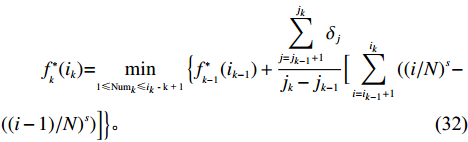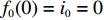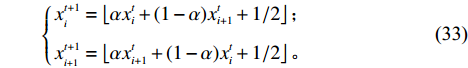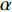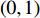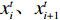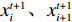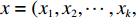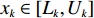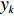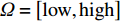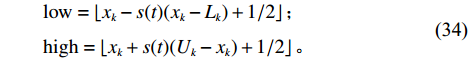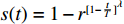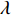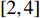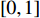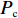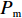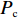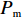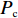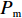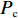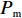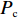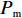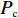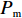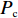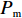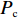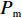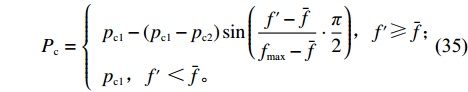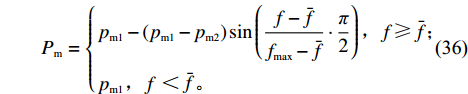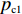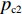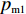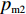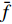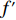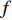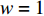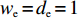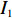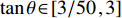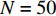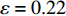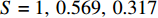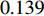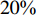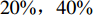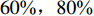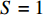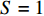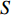A Layout Optimal Method of Fishbone Warehouse Considering Space Sharing Effect
-
摘要:
以Fishbone仓储布局为基础,针对3种经典存储策略,考虑货位共享效应,以单程平均货物拣选距离最短为目标,建立Fishbone布局仓库设计优化模型,以探讨将货位共享效应考虑在内时,不同存储策略对仓储布局的影响;采用分次逼近策略和动态规划算法确定货物的优化分类及类别边界;设计基于自适应的遗传算法获得最优存储分类下的仓储布局参数,并结合案例实验数据进行仿真分析。结果表明,基于分类存储策略的仓储布局表现优异,所需货位数量少且货物拣选距离短;另外,仓储存储物品的需求差异越大,考虑货位共享效应的优势就越显著,最高可减少37.1%的货物拣选距离。
-
关键词:
- Fishbone布局 /
- 货位共享效应 /
- 分次逼近策略 /
- 动态规划 /
- 自适应遗传算法
Abstract:Fishbone layout warehouse is formed by inserting two main channels in the traditional rectangular warehouse, which has obvious advantages in sorting efficiency. Based on the Fishbone warehouse layout, an optimization model of Fishbone warehouse design was established to investigate the effects of different storage strategies on the warehouse layout when the space sharing effect was taken into account and the minimum one-way average picking distance. A gradational approximation strategy and dynamic programming algorithm were used to determine the optimal classification and class boundary. And then an adaptive genetic algorithm was designed to obtain the optimization storage layout parameters under the optimization storage classification. A simulation analysis was conducted based on the experimental data of the case. The results show that the warehouse layout based on the classification storage strategy performs well, and less space is required and the picking distance of goods is smaller. In addition, the greater the demand difference of goods stored in the warehouse is, the more significant the advantage of considering the space sharing effect is, which can reduce the picking distance of goods by up to 37.1%.
-
近年来,国际竞争日益激烈,德国提出“工业4.0”以来,各国纷纷出台相关政策。我国战略性布局“中国制造2025”,振兴制造业,实现从制造大国向智造强国转变,围绕智能工厂、智能车间、智能仓储、智能物流等主题内容,实现我国制造业提质降本增效的管理目标。仓储物流是制造产业链中重要一环,在制造业以及零售业中扮演着愈发重要的角色。根据仓储运作流程,仓储效率影响因素主要包括仓储布局设计、货位分配以及拣货作业。
仓储布局设计问题长期以来受到国内外学者广泛重视。2009年美国学者Gue等[1]创新仓库布局规则,提出非传统布局方式,并发现在一定的假设条件下,该布局方式能够减少平均10% ~ 20%的移动距离。这种显著优势激发了广大科研人员对仓储布局优化的重新思考,以非传统仓储布局为对象,相关理论研究成果不断丰富。Pohl等[2-3]在Fishbone设计中分析单、双命令操作和基于周转率的存储策略,结果表明,使用随机存储策略获得的最优布局参数用于周转率存储策略时,拣货距离表现同样优异。Öztürkoğlu等[4]在随机存储策略基础上,建立一个连续空间模型,用于分析和优化仓库设计,得到Chevron型、Leaf型、Butterfly型3种非传统布局。Cardona等[5]给出一种基于参数确定三维鱼骨布局的设计方法,以仓储面积成本和货物拣选成本最小为目标,建立仓储布局设计优化模型,采用遗传算法求解。Venkitasubramony等[6]基于精确的多边形轮廓,建立随机、基于分类和全周转率存储策略下Fishbone布局的离散和连续的距离模型。国内方面,张志勇等[7]对现有方法进行改进,提出一种形似两片树叶的双叶Leaf布局方法。蒋美仙等[8]在研究Fishbone布局时结合贯通式货架系统的思想,给出一种改进Fishbone仓库布局方法。
货位分配优化问题是解决如何将货物分配到最“合适”的位置上,以使得仓储效率最大化。其主要涉及到3种存储策略,分别为随机存储策略、分类存储策略和全周转率存储策略(每个类别中存储一种货物)。已有文献对货位分配优化问题进行研究,对于多层货架而言,其主要优化目标为出入库效率最高和货架的重心最低[9]。现有研究大部分是基于“存储货物所需的货位数量等于其平均库存水平”假设条件下,仅探讨基于货物周转率进行多个存储类别的划分,以期带来仓储效率的提高,而忽略了一个存储类别中不同货物之间货位共享效应的降低会导致仓储所需货位个数增加,致使仓储效率降低。Yu等[10]证实仅当一个存储类别中,货物的种类数趋近无穷大时,“存储货物所需的货位数量等于其平均库存水平”这一假设才会成立。而实际仓储运作中,一个存储类别中存储的货物种类数是有限的,因此,在衡量仓储出入库效率时,应同时考虑货物的周转率效益和货位共享效应,目前极少文献考虑这两方面因素。Yu等[10]通过考虑有限数量的物品并放松一定的假设,构建一个拣货时间模型,结果表明更多的存储分类并不是最优的。Guo等[11]在传统矩形仓储中探讨3种存储策略在拣货距离方面的表现时,涉及货位的共享效应,构建平均拣货距离函数模型并进行求解,结果表明,在考虑货位共享时,基于分类的存储策略优于随机存储策略和全周转率的存储策略。Venkitasubramony等[12]研究一种单分区货架的仓库布局设计问题,并在纵向和横向两个维度上都采用基于周转率的仓储分配,在确定仓库规模时,将货位共享效应对仓储空间需求的影响考虑在内。
综上所述,货位共享效应真实存在,考虑共享效应的仓储布局设计在仓储运作管理中扮演着越来越重要的角色,现有文献暂未发现在考虑货位共享效应的前提下,研究3种存储策略对非传统仓储布局设计影响。本文将重点探讨基于货位共享效应的新型Fishbone仓储布局优化设计问题,并给出解决此类型仓储布局问题的方法。
1. 仓储布局设计
1.1 仓储布局
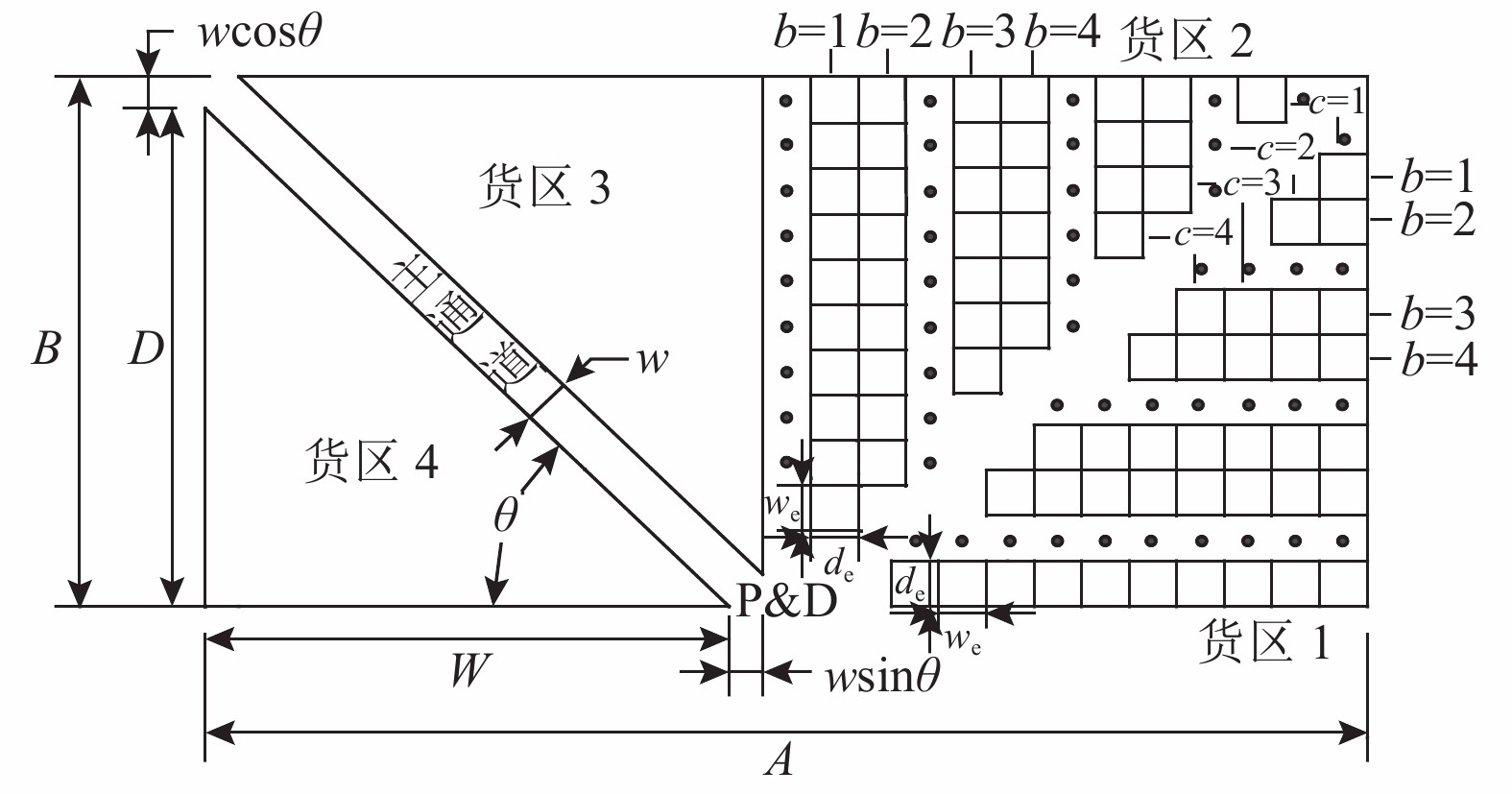
企业土地资源成本上升,仓库设计不合理不仅造成仓库面积利用率不高,而且拣货效率低下。因此,需要设计合理的仓库布局和结构,在尽可能保证仓库面积成本及面积利用率的前提下提高货物存取效率。图1所示是非传统Fishbone型仓库布局,以此进行参数设置,具体见1.2.1中参数说明。
1.2 Fishbone仓储设计
1.2.1 假设条件及参数说明
假设条件如下。
1) 仓储为单元式货架仓库;
2) 采用单命令存取方式,即每次存或取一个货物;
3) 每个货位的几何尺寸一致;
4) 存储货物规格与仓储货位尺寸匹配;
5) 货物周转率已知。
相关参数说明如下。
P&D (pickup and deposit):存取货物点;
$a $ :货区a,$a = 1,2,3,4$ ;b:货区a中第b行货架,
$ b = 1,2,3,\cdots,{N_a} $ ;c:货区a中第b行货架的第c个货位,
$ c = 1,\;2,\; 3,\cdots,{\omega _{ab}} $ ;$w$ :主通道及拣选通道的宽度;$ \theta $ :主通道与拣选通道之间的夹角;W:货区4的宽度;
$ D $ :货区4的深度;$w_{{\rm{e}}}$ :货位的宽度,下标e在文中特指货位;$d_{\rm{e}}$ :货位的深度;$N_{{\rm{f}}}$ :货区1第一行货架中货位的数量,下标f 在文中特指第1行;$ I_{1} $ :货区1内连续两个奇数行货架中货位个数的增量;$ I_{2} $ :当$ b $ 为偶数时,货区1内第$ b $ 行货架相对于第$ b-1 $ 行货架中货位个数的增量;$ \eta $ :货区1中货架行的数量,即$ b $ 的最大取值;$ N_{a} $ :货区$ a $ 中货架行的数量;$ \omega_{a b} $ :货区$ a $ 中第$ b $ 行货架的总货位数量;$ S $ :仓储内总货位数量;$ A $ :仓储的总宽度;$ B $ :仓储的总深度;$ j $ :第$ j $ 个存储位置的序号值,离P&D点距离越近的位置,序号值越小;$ d_{j} $ :仓储P&D点到第$ j $ 个货位的单程移动距离。1.2.2 Fishbone仓储中
$ d_{j} $ 的确定如图1所示,货区1与货区4对称,货区2与货区3对称。以
$N_{{\rm{f}}}$ 、$ I_{1} $ 、$ \eta $ 作为Fishbone仓储优化的自变量,其中$N_{{\rm{f}}}$ 应满足不等式$$ \qquad {N_{\rm{f}}} < \left\lceil {1 + \frac{{{I_1}({d_{\rm{e}}} + {w})}}{{2{d_{\rm{e}}} + {w}}}} \right\rceil 。$$ (1) 依据Fishbone型仓储布局特点,通过以下步骤来确定仓储P&D点到第
$ j $ 个货位的单程移动距离(${d_j}$ ),以用于后续平均拣货距离评估。步骤如下。第1步 确定主通道与拣选通道的角度。
$$\qquad \theta = {\tan ^{ - 1}}\left(\frac{{2{d_{\rm{e}}} + {w}}}{{{I_1}{w_{\rm{e}}}}}\right) 。$$ (2) 第2步 确定增量
$ I_{2} $ 。$$ \qquad {I_2} = \left\lfloor {\frac{{{d_{\rm{e}}}}}{{\tan \theta {w_{\rm{e}}}}}} \right\rfloor 。 $$ (3) 第3步 确定货区
$ a $ 中第$ b $ 行的总货位数$ \omega_{a b} $ 。$$\qquad D = {N_{\rm{f}}}{w_{\rm{e}}}\tan \theta + \eta {d_{\rm{e}}} + \frac{{{w}}}{4}\left[ {2\eta + {{( - 1)}^\eta } - 1} \right] ;$$ (4) $$ \qquad W = \frac{D}{{\tan \theta }}; $$ (5) $$ \begin{split} &\qquad {\omega _{1b}} = {N_{\rm{f}}} + \frac{1}{4}\left[ {2b + {{( - 1)}^b} - 1} \right]{I_2} + \frac{1}{4}\left[ {2b - {{( - 1)}^b} - 3} \right]\times\\ &({I_1} - {I_2}) ;\\[-12pt] \end{split} $$ (6) $$ \qquad{\omega _{2b}} = \left\lfloor {\frac{{\tan \theta }}{{{d_{\rm{e}}}}}\left\{ {W - b{d_{\rm{e}}} - \frac{{{w_p}}}{4}\left[ {2b - {{( - 1)}^b} - 3} \right]} \right\}} \right\rfloor ;$$ (7) $$ \qquad \omega_{a b}= \begin{cases}\omega_{1 b}, a \in\{1,4\}; \\ \omega_{2 b}, a \in\{2,3\}。\end{cases} $$ (8) 第4步 确定货区
$ a $ 中货架的行数:这里先定义$ \gamma $ 为货区2中满足深度为$ W $ 的最大货架行$ b $ 的值。$$ \qquad \gamma = \mathop {\max }\limits_{_q} \left\{ {q{d_{\rm{e}}} + \frac{{{w}}}{4}\left[ {2q + {{( - 1)}^q} - 1} \right] \leqslant W} \right\}; $$ (9) $$ \qquad N_{a}= \begin{cases}\eta , a \in\{1,4\}; \\ \gamma, a \in\{2,3\}。\end{cases} $$ (10) 第5步 设
$\varPhi_{abc}$ 为仓库中一个货位的位置坐标(同一拣选通道两侧相对货位共用一个位置坐标,如图1右侧所示),以仓储左下角为坐标原点,则$\varPhi_{abc} = (X_{abc},Y_{abc})$ 。$$ \qquad A = 2W + {w} + 2{w}\sin \theta ; $$ (11) $$ \qquad B = D + {w}\cos \theta 。 $$ (12) $$ \qquad {X_{abc}} = \left\{ {\begin{array}{*{20}{l}} {A - (c - 0.5){w_{\rm{e}}}},{a = 1}; \\ {\dfrac{A}{2} + \dfrac{{{w} + 2{d_{\rm{e}}}}}{4}\left[ {2b + {{( - 1)}^b} - 1} \right]},{a = 2}; \\ {\dfrac{A}{2} - \dfrac{{{w} + 2{d_{\rm{e}}}}}{4}\left[ {2b + {{( - 1)}^b} - 1} \right]},{a = 3}; \\ {(c - 0.5){w_{\rm{e}}}{\kern 1pt} },{a = 4}。 \end{array}} \right. $$ (13) $$\qquad{Y_{abc}} = \left\{ \begin{aligned} & D - {N_{\rm{f}}}{w_{\rm{e}}}\tan \theta + \frac{{{w_p}}}{2}- \\ & \;\quad\frac{{{w} + 2{d_{\rm{e}}}}}{4}\left[ {2b + {{( - 1)}^b} - 1} \right] ,{a \in \left\{ {1,4} \right\}}; \\ &{B - (c - 0.5){w_{\rm{e}}}},{a \in \left\{ {2,3} \right\}} 。 \end{aligned}\right. $$ (14) 第6步 确定仓储中货位的总个数
$ S $ 。$$ \qquad S =\displaystyle \sum\limits_{a = 1}^4 {\sum\limits_{b = 1}^{N_a} {\omega_{ab}} }。 $$ (15) 第7步 计算仓库中每个货位到P&D点的距离,公式如下。
$$ \qquad {D_{A,\tan \theta }}(x,y) = \left\{ {\begin{array}{*{20}{l}} {D{1_{A,\tan \theta }}(x,y)},{a \in \left\{ {1,4} \right\}}; \\ {D{2_{A,\tan \theta }}(x,y)},{a \in \left\{ {2,3} \right\}}。 \end{array}} \right. $$ (16) $$ \qquad \begin{gathered} D{1_{A,\tan \theta }}(x,y) = |x - 0.5A| + \frac{1}{{\tan \theta }}\left[ {{{\sqrt{1 + {{\tan }^2}\theta }} } - 1} \right]y ; \end{gathered} $$ (17) $$ \qquad \begin{gathered} D{2_{A,\tan \theta }}(x,y) = \left[ {{{\sqrt{1 + {{\tan }^2}\theta }}} - \tan \theta } \right]|x - 0.5A| + y。 \end{gathered} $$ (18) 按照距离值由小到大排序,并将排序结果记为
$ d_{j} $ 。1.2.3 优化模型的建立
参数说明如下。
$ S $ :需求倾斜因子;$ \varepsilon $ :货位共享因子,$ 0 < \varepsilon \leqslant 1 $ ;$ i$ :第i种货物的序号,周转率较低的货物种类具有较大的序号值;$ n $ :存储系统的分类数量;$ k $ :第k类的序号值,k = 1, 2,$ \cdots$ , n;$ i_{k} $ :第k类中周转率最低货物种类的序号值;$ j_k$ :第k类中距离P&D点最远存储位置的序号值,它可表示第1类到第k类所需的总存储货位数量;$ N $ :存储在仓储中货物的种类数;$ t_{k} $ :存储一个货物到k类中或从k类中拣选一个货物的单程平均移动距离;$ D(i) $ :第i种货物在一段时间内的需求量;$ T_{n} $ :n类存储系统中,存/取单个货物的单程平均移动距离。根据给出的符号,基于n类存储系统的平均拣货距离表示为
$$ \qquad {T_n} = \sum\limits_{k = 1}^n {{t_k}} \left[ {\sum\limits_{i = {i_{k - 1}} + 1}^{{i_k}} {(G(i) - G(i - 1))} } \right]。 $$ (19) 其中,
${i_0} = 0$ ;$G(0) = 0$ ;$G(i)$ 为ABC需求函数,可表示为$$ \qquad G(i) = {(i/N)^s} = {\sum\limits_{x = 1}^i D (x)} \left/ {\sum\limits_{x = 1}^N D (x)}\right. 。$$ (20) 其中,
$ 0 {\text{<}} s \leqslant 1 $ 。利用已求得的
$ d_{j} $ ,可求出从P&D点到第$ k $ 类所有货位的平均距离,即存储(或拣选)一个属于第$ k $ 类的货物时。单程平均移动距离可计算为$$\qquad t_{k}=\frac{1}{j_{k}-j_{k-1}} \sum_{j=j_{k-1}+1}^{j_{k}} d_{j} 。$$ (21) 其中,
$ {j}_{0}=0 $ 。仓储系统的单程平均货物拣选距离为$$ \qquad {T_n} = \sum\limits_{k = 1}^n {\dfrac{{\displaystyle\sum\limits_{j = {j_{k - 1}} + 1}^{{j_k}} {{d_j}} }}{{{j_k} - {j_{k - 1}}}}} \left\{ {\sum\limits_{i = {i_{k - 1}} + 1}^{{i_k}} {\left[ {{{(i/N)}^s} - {{\left( {(i - 1)/N} \right)}^s}} \right]} } \right\} 。 $$ (22) 通过计算所需货位个数能够找到
$ j_k$ 与$ i_k$ 的关系。存储在k类中的货物i所需的存储空间可以表示为$$ \qquad{a_i}\left( {{\rm{Num}}_k} \right) = \left\lceil {0.5(1 + {\rm{Num}}_k^{ - \varepsilon })Q(i)} \right\rceil 。$$ (23) 式(23)中,
${\rm{Num}}_{k}$ 表示存储在第k类中货物的种类数。Yu等[10]、Guo 等[11]表明$ \varepsilon $ 对其影响因素的变化极不敏感,而且$ \varepsilon $ 值基本都处于0.15和0.25之间,最为常用的是$ \varepsilon $ = 0.22。因此,本文也采用$ \varepsilon $ 的平均值0.22来讨论Fishbone型仓储的货位共享效应。根据上述表示,第k类中存储
$ i_{k}-i_{k-1} $ 种物品所需的存储空间为$$ \qquad {R_k} = \sum\limits_{i = {i_{k - 1}} + 1}^{{i_k}} {{a_i}} \left( {{\rm{Num}}_k} \right) = \left\lceil {0.5(1 + {\rm{Num}}_k^{ - \varepsilon }) \sum\limits_{i = {i_{k - 1}} + 1}^{{i_k}} {Q(i)} } \right\rceil。 $$ (24) 这里考虑经典的经济订货批量(EOQ),即
$$\qquad Q(i) = \sqrt {2KD(i)}。 $$ (25) 其中,
$ \ K $ 表示再订货成本与持有成本之比,为了便于处理,这里假定为常数。令所有存储在仓库中的货品总需求为R,使得$R =\displaystyle \sum\limits_{x = 1}^N D (x)$ 。货物i的需求可以表示为$$ \qquad \begin{gathered} D(i) = R\left\{ {{{(i/N)}^s} - {{\left[ {(i - 1)/N} \right]}^s}} \right\}, {\kern 1pt} i = 1,2, \cdots ,N 。 \end{gathered} $$ (26) 前k个存储类的累计所需空间是每个存储类所需空间之和。
$$ \qquad {j_k} = \sum\limits_{l = 1}^k {{R_l}}。 $$ (27) 所以,单程平均拣货距离优化模型可以建立为
$$ \qquad {\rm{min}}\;{T_n} = \sum\limits_{k = 1}^n {\dfrac{{\displaystyle\sum\limits_{j = {j_{k - 1}} + 1}^{{j_k}} {{d_j}} }}{{{j_k} - {j_{k - 1}}}}\left\{ {\sum\limits_{i = {i_{k - 1}} + 1}^{{i_k}} {\left[ {{{(i/N)}^s} - {{\left( {(i - 1)/N} \right)}^s}} \right]} } \right\}} ;$$ (28) $$ \qquad \begin{split} &{\text{s}}{\text{.t}}{\text{. }}\\ &{j_k} = \left\lceil {\sqrt {0.5K} \sum\limits_{l = 1}^k {\left[ {\left( {1 + {\rm{Num}}_l^{ - \varepsilon }} \right)\sum\limits_{i = {i_{l - 1}} + 1}^{{i_l}} {\sqrt {D(i)} } } \right]} } \right\rceil; \end{split} $$ (29) $$ \qquad S \geqslant j_n;$$ (30) $$\qquad i_k\text{>}i_{k-1},i_k\text{>}0, k = 1,2, \cdots ,n,{i_0} = 0 ,{j_{0 }} = 0 。 $$ (31) 目标函数式(28)表示单程平均拣货距离最短;约束条件式(29)表示
$ j_{k} $ 与$ i_k $ 之间的关系;约束条件式(30)表示仓储所提供的货位数量大于或等于存储一定数量货物所需的货位总数;约束条件式(31)表示一个存储类别中至少存储一种货物。2. Fishbone仓储布局优化方法
2.1 分次逼近策略
Fishbone仓储结构难点在于分拣路径的不确定性会导致拣货距离建模困难。通过将各个货位到P&D点距离进行排序的方式虽可实现模型建立,但是需要每次提前获得最优存储策略下满足要求的最小总货位数量,以此优化
$ d_{j} $ ,从而确定出最优存储分类数量及类别边界,否则会因误差过大导致所求的优化解并非最优。因此,为了解决此问题,本文采用分次逼近策略,步骤如下。第1步 初始化一个较大的C值,通过式(27)初步获得近似最优的所需货位数量,得到此结构下N 种分类中最大的货位数以第1次优化
$ d_{j} $ ;第2步 利用第1步得到的
$ d_{j} $ ,可以获得此结构下近似最优的货物分类数量$ n$ ,并第2次优化$ d_{j} $ 。第3步 通过搜寻
$ n+1 $ 个类中的最小单程平均拣货距离,从而获得精确的$ T_{n} $ 值、最优存储分类数量及每个类别中货物的种类数。2.2 动态规划算法设计
当
$n = 1$ 或$n = N$ 时,可直接代入式(27)和式(28)计算得出仓储所需货位数量及平均拣货距离,其他情况的求解可通过动态规划算法帮助完成,以获得相应的分类数量及其类别边界。步骤如下。1) 确定阶段
$ k $ :与仓储中第$ k $ 个类别相对应;2) 确定决策变量:
${\rm{Num}}_k$ ,其取值范围为$\left\{ {\rm{Num}}_k|1 \leqslant {\rm{Num}}_k \leqslant {i_k}{{ - k + 1}} \right\}$ ;3) 确定状态转移方程:
${i_k} = {\rm{Num}}_k + {i_{k - 1}}$ ,$\left\{ {i_k}| k \leqslant {i_k} \leqslant N - (n - k) \right\}$ ,因为每个存储类中至少存在一个货物类;4) 指标函数:
${f_k}({i_k})$ ,所以第k阶段与k−1阶段的递推关系式可以写为(第2类到第n-1类);$$ \begin{split}&\qquad f_{_k}^ * ({i_k}) = \mathop {{\rm{min}}}\limits_{_{1 \leqslant {\rm{Num}}_k \leqslant {i_k}{\text{ - k + 1}}}} \Big\{f_{_{k - 1}}^ * ({i_{k - 1}}) + \frac{{\displaystyle\sum\limits_{j = {j_{k - 1}} + 1}^{{j_k}} {{\delta _j}} }}{{{j_k} - {j_{k - 1}}}}\Big[ \sum\limits_{i = {i_{k - 1}} + 1}^{{i_k}} {({{{(i/N)}^s} -}}\Big.\Big.\\ &\Big.\Big.{{{{( {(i - 1)/N} )}^s} )}} \Big]\Big\} 。 \end{split} $$ (32) 5) 初始化条件:
$ f_{0}(0)=i_{0}=0 $ 。2.3 基于自适应的遗传算法设计
2.3.1 遗传算法
遗传算法主要用于处理优化问题,然而标准的遗传算法也存在着诸如进化初期存在“早熟”、进化末期难收敛等问题[13]。因此,设计自适应遗传算法(adaptive genetic algorithm,AGA),采用动态自适应策略,对算法的交叉、变异算子进行改进,并且在算法后期插入一个小种群的最优个体,使得算法具备跳出局部最优解的能力。本文以单程平均拣货距离函数的倒数作为适应度函数。
2.3.2 整数编码
整数编码方式无需进行编码和解码操作,能够很大程度上提高解的精度以及收敛速度;便于在大空间内搜索,而且还能避免二进制编码导致的海明悬崖(Hamming cliffs)问题。另外,遗传算法的整数编码策略用于解决离散变量的寻优问题时表现优异[14],基于上述分析,再加上本问题的特征,这里采用整数编码方式。
2.3.3 操作算子
选择算子。选择算子的作用主要是使适应度值高的个体能更大可能性被选中,有更大机会作为父代,从而提高遗传算法的计算效率和效果。选择算子采用轮盘赌法进行个体选择。
交叉算子。交叉算子是遗传算法区别于其他优化算法的本质特征,通过交叉组合的方式产生新的个体,同时也降低了对表现优异父代特征的破坏程度,从而起到全局搜索寻优的效果。采用整数编码的交叉算子可以表示为
$$ \qquad \left\{ \begin{gathered} x_{_i}^{t + 1} = \left\lfloor {\alpha x_i^t + (1 - \alpha )x_{i + 1}^t + 1/2} \right\rfloor ; \\ x_{_{i + 1}}^{t + 1} = \left\lfloor {\alpha x_{i + 1}^t + (1 - \alpha )x_i^t + 1/2} \right\rfloor 。 \\ \end{gathered} \right. $$ (33) 其中,
$ \alpha $ 为参数,取值范围为$ (0,1) $ ;$x_i^t、x_{i + 1}^t$ 表示交叉前的父代个体对;$x_i^{t + 1}、x_{i + 1}^{t + 1}$ 表示交叉后的子代个体对。变异算子。通过以上交叉操作方式保持群体多样性是有条件的,此时变异操作就成为弥补算法缺陷的有效策略[15] 。假设父代的染色体
$x =({x_1},{x_2},\cdots,{x_k}, \cdots, {x_n})$ ,并设元素$ {x_k} \in \left[ {{L_k},{U_k}} \right] $ 为变异元素,变异后的元素$ y_{k} $ 将随机产生于区间${{\varOmega}}$ :${{\varOmega}} = \left[ {{\rm{low}},{\rm{high}}} \right]$ 。$$ \qquad \begin{gathered} {\rm{low}} = \left\lfloor {{x_k} - s(t)({x_k} - {L_k}) + 1/2} \right\rfloor ; \\ {\rm{high}} = \left\lfloor {{x_k} + s(t)({U_k} - {x_k}) + 1/2} \right\rfloor 。 \\ \end{gathered} $$ (34) 其中,
$ s(t) = 1 - {r^{{{[1 - \frac{t}{T}]}^\lambda }}} $ ;T为进化的最大迭代数;$ \lambda $ 为参数,取值一般为$[2,4]$ ;r为参数,取值为$[0,1]$ 。2.3.4 自适应策略
Srinivas等[16]提出一种自适应遗传算法,主要是通过适应度值自动改变其中的交叉概率
$P_{{\rm{c}}}$ 和变异概率$ P_{{\rm{m}}} $ 。其具体思想体现为当种群个体的适应度值趋于一致时,交叉概率$P_{{\rm{c}}}$ 和变异概率$P_{{\rm{m}}}$ 增大,以增强种群跳出局部最优解的能力;而当群体的适应度值相对分散时,$P_{{\rm{c}}}$ 和$P_{{\rm{m}}}$ 减小,以使种群能够迅速收敛。与此同时,对于种群中一些适应度值高于群体平均适应度值的个体,$P_{{\rm{c}}}$ 和$P_{{\rm{m}}}$ 较小,使这些个体能进入下一代;而对于低于平均适应度值的个体,$P_{{\rm{c}}}$ 和$P_{{\rm{m}}}$ 较大,该个体将被淘汰。因此,自适应策略中的$ P_{{\rm{c}}} $ 和$ P_{{\rm{m}}} $ 能够自动匹配最佳$P_{{\rm{c}}}$ 和$P_{{\rm{m}}}$ 给对应的个体,可以看出,该策略能够实现在保持群体多样性的同时,保证遗传算法的收敛性。本文提出交叉概率$P_{{\rm{c}}}$ 和变异概率$P_{{\rm{m}}}$ 计算公式如下。$$ \qquad {P_{\rm{c}}} = \left\{ {\begin{array}{*{20}{l}} {{p_{{\rm{c}}1}} - ({p_{{\rm{c}}1}} - {p_{{\rm{c}}2}}) \sin \left( {\dfrac{{{f^\prime } - \mathop f\limits^\_ }}{{{f_{\max }} - \mathop f\limits^\_ }} \cdot \dfrac{\pi }{2}} \right)},{{f^\prime } \geqslant \mathop f\limits^\_ }; \\ {{p_{{\rm{c}}1}}} ,{{f^\prime }{\text{ < }}\mathop f\limits^\_ }。 \end{array}} \right. $$ (35) $$ \qquad{P_{\rm{m}}} = \left\{ \begin{gathered} {p_{{\rm{m}}1}} - ({p_{{\rm{m}}1}} - {p_{{\rm{m}}2}}) \sin \left( {\frac{{f - \mathop f\limits^\_ }}{{{f_{\max }} - \mathop f\limits^\_ }} \cdot \frac{\pi }{2}} \right) ,{f \geqslant \mathop f\limits^\_ }; \\ {p_{{\rm{m}}1}},{f{\text{ < }}\mathop f\limits^\_ }。 \\ \end{gathered} \right. $$ (36) 式中,
$ p_{{\rm{c}} 1} $ 、$ p_{{\rm{c}} 2} $ 分别设定为交叉概率的最大值和最小值;$ p_{{\rm{m}} 1 } $ 、$ p_{{\rm{m}} 2} $ 分别设定为变异概率的最大值和最小值;$ f_{{\rm{max}}}$ 为每代群体中最大的适应度值;$\mathop f\limits^\_$ 为每代群体的平均适应度值;$ f^{\prime} $ 为两个要进行交叉操作个体中较大的适应度值;$ f$ 为变异个体的适应度值。3. 仿真实验
3.1 实验参数设定
设Fishbone型布局仓储主通道和拣选通道的宽度均为1 m,即
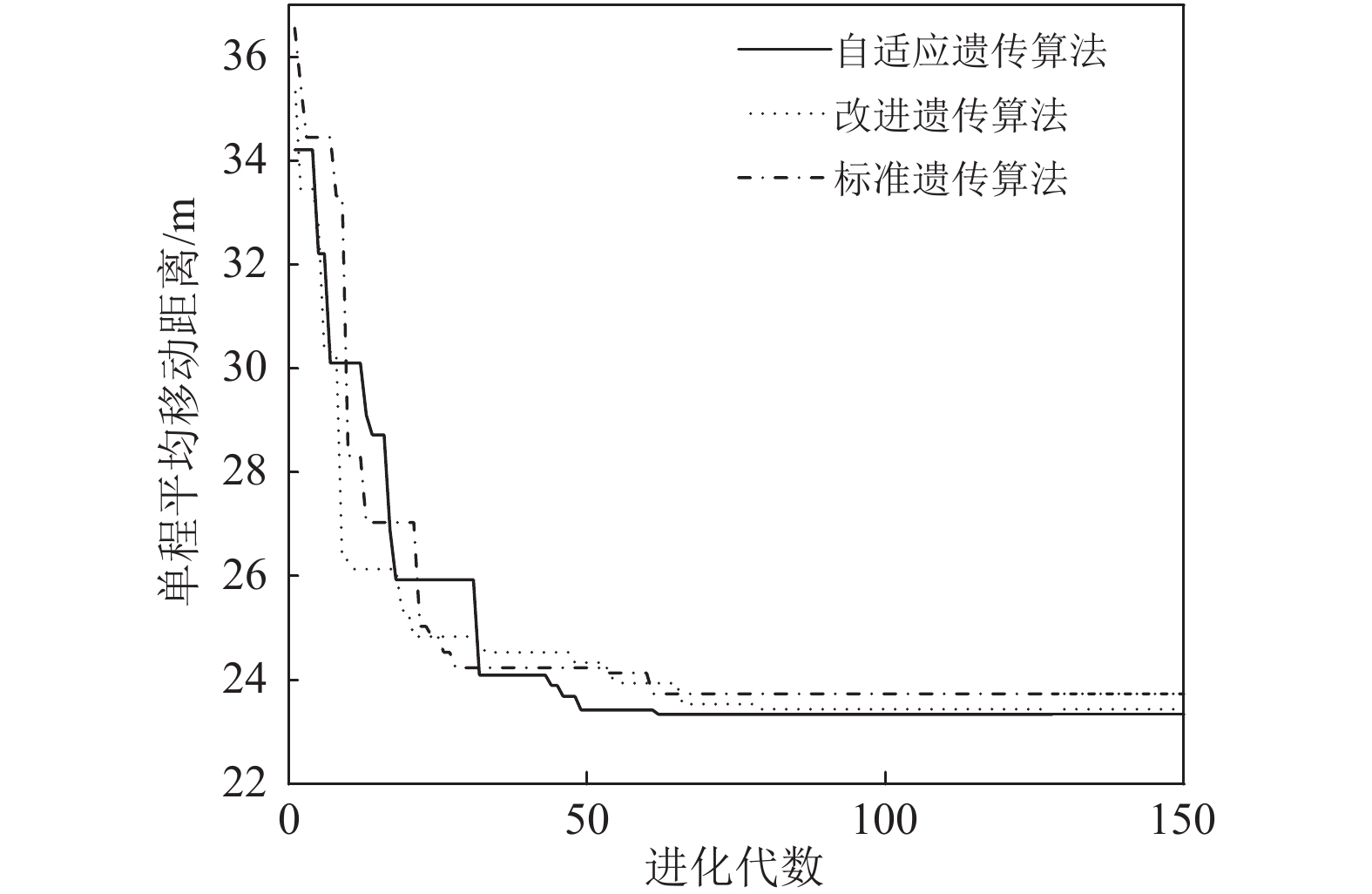
${w} = 1$ ;仓储中货位是宽深度均为1 m的正方形,${w_{\rm{e}}} = {d_{\rm{e}}} = 1$ ;$ I_{1} $ 取值为[1,50],有$\tan \theta \in [3 / 50\,, 3]$ ;仓储中货物的种类数$ N=50 $ ;这里假定实验的周期是以月为单位,并假定一个月内的货物总需求R =10000 ;订货成本与持有成本的比值K = 2;货位共享因子$\varepsilon=0.22$ ;需求倾斜因子由大到小分别取$ S = 1,\;0.569,\;0.317 $ ,$0.139$ ,分别表示$ 20 {\text{%}} $ 的货物量贡献了$ 20 {\text{%}} ,40 {\text{%}} $ ,$ 60 {\text{%}},80 {\text{%}} $ 的货物需求[11]。为了验证上述所提算法的有效性,将对基于自适应的遗传算法、文献[17]提出的改进遗传算法以及标准遗传算法进行对比分析及验证。3种算法主要参数设定种群大小为20,进化代数为150代,标准遗传算法以及改进遗传算法的交叉概率为0.7,变异概率为0.01;自适应遗传算法的交叉概率最大值为0.9,最小值为0.6;变异概率最大值为0.1,最小值为0.01。
3.2 仿真结果
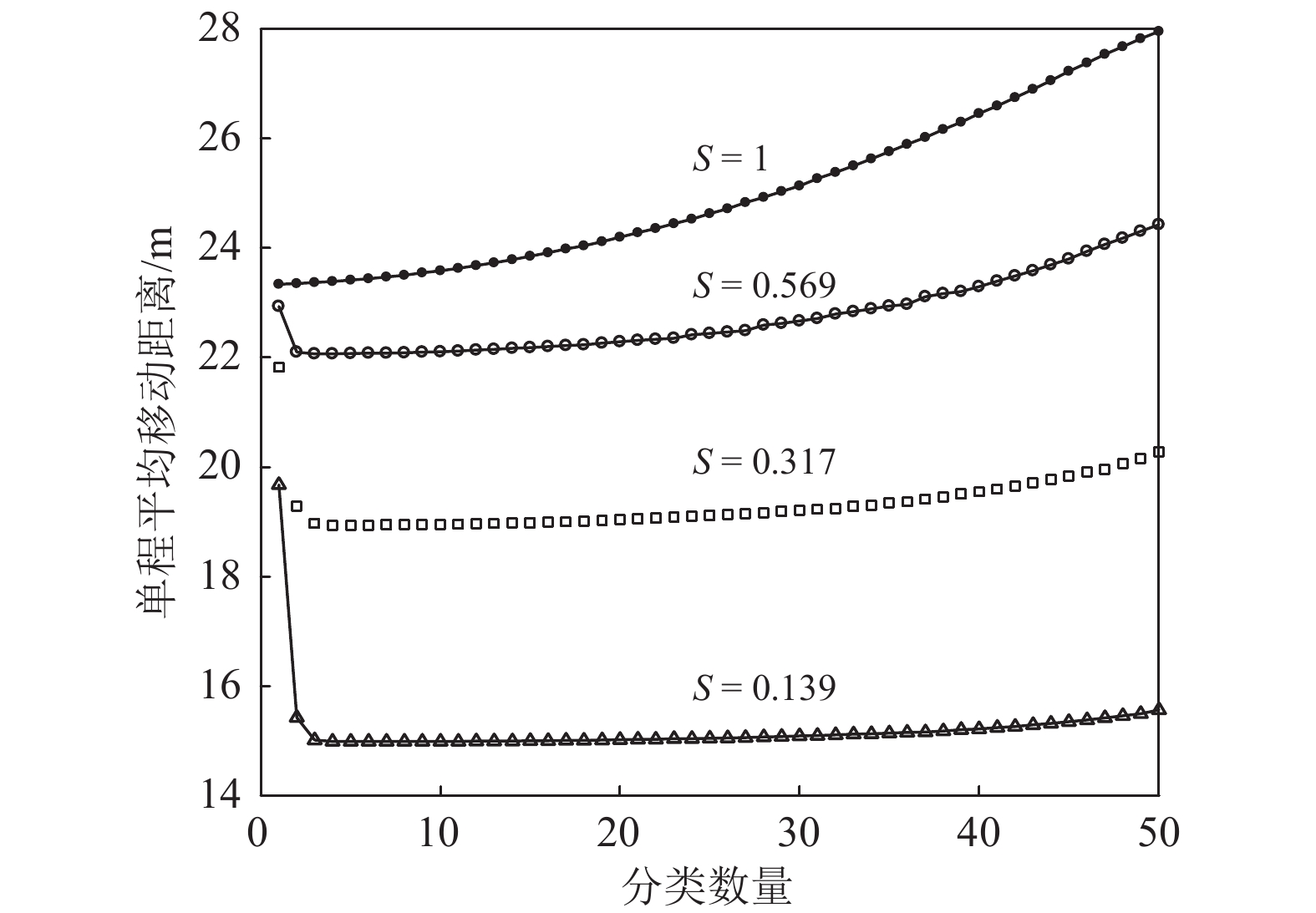
图2给出需求倾斜因子
$ S=1 $ 时,基于自适应遗传算法、改进遗传算法以及标准遗传算法的平均移动距离变化曲线。三者前期逐步跳出局部最优解,基于自适应遗传算法相比于改进遗传算法和标准遗传算法,收敛速度和最优值搜寻表现更为优异,能够更有效地找到最优解。由图3可知,除
$S=1 $ 外,多个ABC需求倾斜因子的最优单程平均移动距离都随着分类数量的增加先减小后增加,且在最优类附近的平均拣货距离对分类数量的变化不敏感。此外,在考虑货位共享效应的前提下,基于分类的存储策略在拣货距离上表现优于全周转率的存储策略。表1给出4种需求倾斜因子所对应的最优分类数量及每个类别的货物种类数。在实际运用时可参考此表中的分类数量及相应的类别边界进行货物的分类存储,以获得成本优势。
表 1 最优分类数量及每个类别的货物种类数Table 1. The optimal number of categories and the number of categories of goods in each category需求倾斜
因子 $ S$数量 类1 类2 类3 类4 类5 1 1 50 0.569 3 8 38 4 0.317 4 1 10 27 12 0.139 5 1 6 19 22 2 由表2可知,随着需求倾斜因子的减小,平均拣货距离是减小的,所需的货位数量也有着减少的趋势。说明当仓储存储的货品需求差异变大时,考虑货位共享效应的优势就越明显,可以带来更多的成本节约。
表 2 最优分类时的最优目标函数值Table 2. The optimal objective function value for optimal classification需求倾斜
因子 $ S$平均拣货距离/m 所需货位数 1 23.34 1007 0.569 21.84 1030 0.317 18.97 968 0.139 14.68 800 通过表3可知,Fishbone布局在不同的
$ S $ 参数值下,仓储的最优结构相差不大,仅是货架行的数量由于所需货位数量不同而不同。因而当货物需求发生改变时,仓储的原有布局结构同样可以获得较为理想的结果。表 3 获得最优目标函数值时仓储的布局参数Table 3. The layout parameters of the warehouse when the optimal objective function value is obtained需求倾斜因子 $ S$ ${\rm{tan}}{\theta}$ $N_{\rm{f}}$ $ I_1$ $ I_2$ $ \eta $ $ B/A$ 1 1 1 3 1 22 0.49 0.569 1 1 3 1 19 0.49 0.317 1 2 3 1 18 0.49 0.139 1 1 3 1 17 0.49 4. 结论
本文在Fishbone布局中考虑货位共享效应,以单程平均货物拣选距离最短为目标,提出分次逼近策略,并设计动态规划算法与自适应遗传算法;探讨随机、基于分类以及全周转率的存储策略对仓储布局的影响。结果表明,在考虑货位共享效应的前提下,Fishbone仓储布局中基于分类存储策略的拣货距离优于全周转率策略,且最优分类的数量较少,最优分类数附近的平均拣货距离对类的变化不敏感;而且,货品的需求倾斜因子S越小,使用基于分类存储策略就越有效,函数目标值就越小,可带来的成本优势就越显著,基于以上4种需求倾斜因子,最高可缩短37.1%的单程平均货物拣选距离。此外,根据本文所提方法设计的仓储,当货物需求发生变化时,原有的仓储结构仍然适用。
本研究今后探讨双命令模式下的布局设计方法;以及解决具有多个P&D点的Fishbone仓储布局设计问题。
-
表 1 最优分类数量及每个类别的货物种类数
Table 1 The optimal number of categories and the number of categories of goods in each category
需求倾斜
因子 S数量 类1 类2 类3 类4 类5 1 1 50 0.569 3 8 38 4 0.317 4 1 10 27 12 0.139 5 1 6 19 22 2 表 2 最优分类时的最优目标函数值
Table 2 The optimal objective function value for optimal classification
需求倾斜
因子 S平均拣货距离/m 所需货位数 1 23.34 1007 0.569 21.84 1030 0.317 18.97 968 0.139 14.68 800 表 3 获得最优目标函数值时仓储的布局参数
Table 3 The layout parameters of the warehouse when the optimal objective function value is obtained
需求倾斜因子 S tanθ Nf I1 I2 η B/A 1 1 1 3 1 22 0.49 0.569 1 1 3 1 19 0.49 0.317 1 2 3 1 18 0.49 0.139 1 1 3 1 17 0.49 -
[1] GUE K R, MELLER R D. Aisle configurations for unit-load warehouses[J]. IIE Transactions, 2009, 41(3): 171-182. DOI: 10.1080/07408170802112726
[2] POHL L M, MELLER R D, GUE K R. Optimizing Fishbone aisles for dual-command operations in a warehouse[J]. Naval Research Logistics (NRL), 2009, 56(5): 389-403. DOI: 10.1002/nav.20355
[3] POHL L M, MELLER R D, GUE K R. Turnover-based storage in non-traditional unit-load warehouse designs[J]. IIE Transactions, 2011, 43(10): 703-720. DOI: 10.1080/0740817X.2010.549098
[4] ÖZTÜRKOĞLU Ö, GUE K R, MELLER R D. Optimal unit-load warehouse designs for single-command operations[J]. IIE Transactions, 2012, 44(6): 459-475. DOI: 10.1080/0740817X.2011.636793
[5] CARDONA L F, SOTO D F, RIVERA L, et al. Detailed design of Fishbone warehouse layouts with vertical travel[J]. International Journal of Production Economics, 2015, 170: 825-837. DOI: 10.1016/j.ijpe.2015.03.006
[6] VENKITASUBRAMONY R, ADIL G K. Analytical models for pick distances in Fishbone warehouse based on exact distance contour[J]. International Journal of Production Research, 2016, 54(14): 4305-4326. DOI: 10.1080/00207543.2016.1148277
[7] 张志勇, 王琴, 梁艳. 仓库内部布局的双叶Leaf方法及其通道角度优化[J]. 系统工程, 2019, 37(2): 70-80. ZHANG Zhiyong, WANG Qin, LIANG Yan. Twin leaf method for warehoure internal layout and its aisles angle optimization[J]. Systems Engineering, 2019, 37(2): 70-80.
[8] 蒋美仙, 冯定忠, 赵晏林, 等. 基于改进Fishbone的物流仓库布局优化[J]. 系统工程理论与实践, 2013, 33(11): 2920-2929. DOI: 10.12011/1000-6788(2013)11-2920 JIANG Meixian, FENG Dingzhong, ZHAO Yanlin, et al. Optimization of logistics warehouse layout based on the improved Fishbone layout[J]. Systems Engineering - Theory & Practice, 2013, 33(11): 2920-2929. DOI: 10.12011/1000-6788(2013)11-2920
[9] 胡颖聪, 刘建胜, 张有功. 基于AGA与MPSO的非传统布局仓储货位分配优化[J]. 高技术通讯, 2012, 28(Z2): 980-990. HU Yingcong, LIU Jiansheng, ZHANG Yougong. Storage location assignment optimization in non-traditional warehouse base on AGA and MPSO[J]. High-tech Communications, 2012, 28(Z2): 980-990.
[10] YU Y, DE KOSTER R B M, GUO X. Class-based storage with a finite number of items: using more classes is not always better[J]. Production and Operations Management, 2015, 24(8): 1235-1247. DOI: 10.1111/poms.12334
[11] GUO X, YU Y, DE KOSTER R B M. Impact of required storage space on storage policy performance in a unit-load warehouse[J]. International Journal of Production Research, 2016, 54(8): 2405-2418. DOI: 10.1080/00207543.2015.1083624
[12] VENKITASUBRAMONY R, ADIL G K. Design of an order-picking warehouse factoring vertical travel and space sharing[J]. The International Journal of Advanced Manufacturing Technology, 2017, 91(5-8): 1921-1934. DOI: 10.1007/s00170-016-9879-3
[13] 邹进. 自适应逐次逼近遗传算法及其在水库群长期调度中的应用[J]. 系统工程理论与实践, 2013, 33(1): 267-272. DOI: 10.3969/j.issn.1000-6788.2013.01.035 ZOU Jin. Adaptive genetic algorithm successive approximation and its application to long-term reservoirs operation[J]. Systems Engineering Theory and Practice, 2013, 33(1): 267-272. DOI: 10.3969/j.issn.1000-6788.2013.01.035
[14] 杨洋, 代文猛, 年春波. 基于自适应遗传算法的层合板铺层优化设计[J]. 机械制造与自动化, 2020, 49(3): 22-25. DOI: 10.19344/j.cnki.issn1671-5276.2020.03.006 YANG Yang, DAI Wenmeng, NIAN Chunbo. Optimal design of composite laminates based on adaptive genetic algorithm[J]. Machinery Manufacturing and Automation, 2020, 49(3): 22-25. DOI: 10.19344/j.cnki.issn1671-5276.2020.03.006
[15] 管小艳. 实数编码下遗传算法的改进及其应用[D]. 重庆: 重庆大学, 2012. GUAN Xiaoyan. Improvement of real-coding genetic algorithm and its applications[D]. Chongqing: Chongqing University, 2012.
[16] SRINIVAS M, PATNAIK L M. Adaptive probabilities of crossover and mutation in genetic algorithms[J]. Systems Man and Cybernetics, 1994, 24(4): 656-667.
[17] 陈晓艳, 张东洋, 苏学斌, 等. 基于改进遗传算法和多目标决策的货位优化策略[J]. 天津科技大学学报, 2020, 35(4): 75-80. DOI: 10.13364/j.issn.1672-6511.20190109 CHEN Xiaoyan, ZHANG Dongyang, SU Xuebin, et al. Cargo location optimization strategy based on improved genetic algorithm and multi-objective decision[J]. Journal of Tianjin University of Scienceand Technology, 2020, 35(4): 75-80. DOI: 10.13364/j.issn.1672-6511.20190109
-
期刊类型引用(0)
其他类型引用(22)



 下载:
下载: