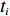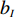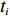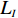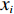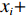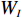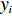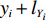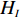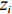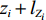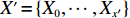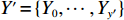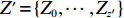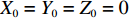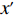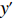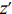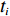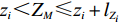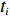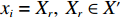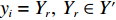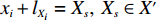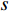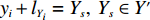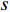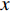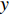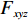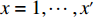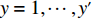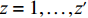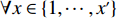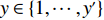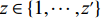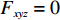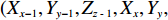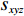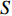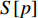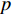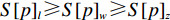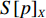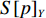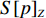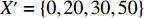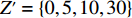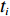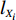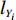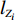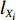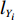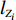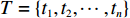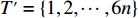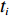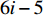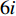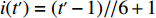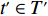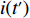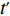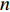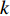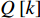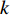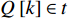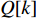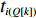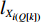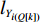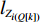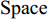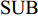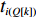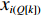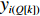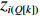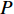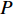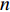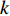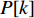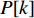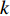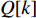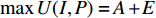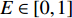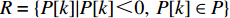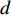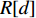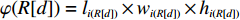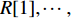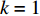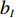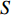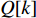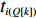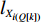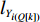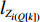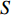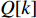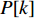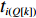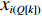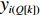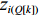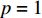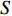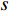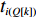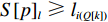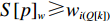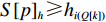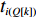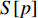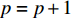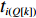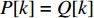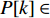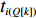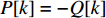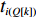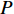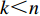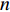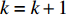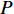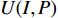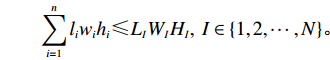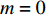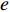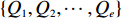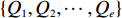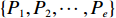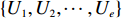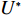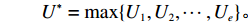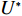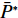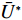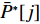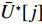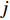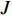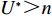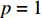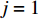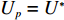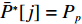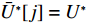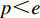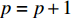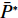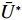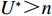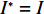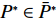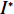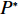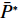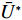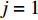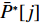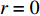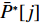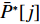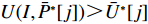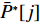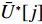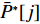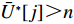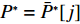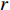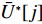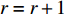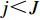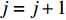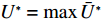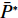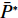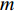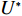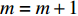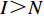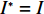A Three-Dimensional Packing Algorithm Based on Spatial Matrix under the Background of E-commerce Logistics
-
摘要:
针对电子商务领域中普遍存在的具有高度个性化和强异构性的三维装箱问题,提出一种电商物流领域适用性极强的组合启发式算法。根据问题特点,首先提出三维装箱的空间矩阵表征方式,基于该表征方式设计优化装箱检验算法,其次优化设计启发式算法的编码译码规则,并引入大规模邻域搜索算法进一步优化装箱序列路径搜索过程,从而共同构成组合启发式算法。结果表明,该算法在电商物流领域装箱问题中性能较好,求解结果接近理论最优解,同时求解质量优于其他装箱算法和商用软件,尤其是在复杂程度较高的装箱问题中更为明显。该算法能有效解决当前研究较少、需求较高的电商物流领域装箱问题,从而极大地降低电商物流企业的装箱成本。
Abstract:Aiming at the highly personalized and heterogeneous three-dimensional packing problem in the field of e-commerce, a combinatorial heuristic algorithm with strong applicability in the field of e-commerce logistics is proposed. According to the characteristics of packing problems, firstly, a spatial matrix representation of three-dimensional packing was proposed, and based on this representation, an optimized packing inspection algorithm was designed. Secondly, the coding and decoding rules of the heuristic algorithm were optimized, and the large-scale neighborhood search algorithm was introduced to further optimize the path search process of the packing sequence. The experimental results show that the algorithm has good performance in the field of e-commerce logistics packing problem. The solution result is extremely close to the theoretical optimal solution, and the solution quality is better than other packing algorithms and commercial software, especially in more complex packing problems. This algorithm can effectively solve the packing problem in the field of e-commerce logistics with less research and higher demand, thus greatly reducing the packing cost and packaging waste of e-commerce logistics enterprises.
-
装箱问题是一种具有复杂约束条件的离散组合优化问题,具有很强的应用背景。到目前为止,有大量关于装箱问题的研究,并有很多文献对此进行解决方法阐述。这些装箱算法大部分都是关于品类少、单项数量多、弱异构性的装箱问题。随着电子商务应用与供给需求不断改善发展,个性化程度高的电商领域装箱订单越来越多,强异构性装箱问题成为其中重要部分,对传统的装箱算法提出新的要求。本文的研究对象为电商领域中的多箱型三维装箱问题 (three-dimensional multiple bin-size bin packing problem, 3D-MBSBPP)。
近些年来,3D-MBSBPP已经有了一定的研究,主要集中在结构假定方式和启发式算法的优化上。在结构假定方式优化方面,大致可分为关键点法[1]、分层法[2]以及空间分割法[3],主要关注如何确定物品在箱子内的可摆放位置以及有多个可摆放位置时如何进行选择。在启发式算法优化方面,大量学者从不同方面进行深入研究。Eley[4]首次提出集合覆盖模型,以模型的每一列对应一种装箱方案,并提出相应的基于树搜索启发式算法的列生成算法。随着该模型的提出,各种列生成算法不断涌现,其中启发式算法为首选。例如,Sulaiman等[5]提出一种基于随机交叉和动态变异的遗传算法,以克服早熟收敛。Fu等[6]基于优先级队列分支的思想和约束方法,提出一种分支定界算法。Dell'Amico等[7]在研究了多项式大小公式、指数大小公式以及若干下界上界的基础上,提出一种求解指数型公式的分支价格算法。Li等[8]提出一种基于差分进化算子的入侵杂草优化算法。Fan等[9]根据算法编码的特点,设计一种替换插入的方法并更新了交叉算子,从而提出一种改进的分组遗传算法。此外,国内学者在启发式算法优化方面也取得很好的结果,如在遗传算法[10]、模拟退火算法[11]、蚁群算法[12]等方面。
以上这些算法都假定装填结果满足一定的结构,虽然简化了装填过程,但造成搜索解空间变小,从而导致解的质量不高。而且,电商物流订单具有高度个性化特点,主要体现在由于电商订单均为客户定制订单,订单个体呈现出各品类间物品数量波动大的特点。因此,传统装箱问题的结构假定方式,如砌墙、建堆、立方体排列、切割等,不适用于电商物流。同时,大规模邻域搜索算法是作为一种高效寻优算法,既能保持大规模邻域的寻优能力,又能克服低效耗时的弱点,如在TSP问题研究中,贾瑞玉等[13]就通过引入大规模邻域搜索算法优化传统启发式算法的搜索路径并取得良好效果。而在三维装箱问题中,由于大规模邻域搜索算法的关键元素较难选择,该算法之前并未用于装箱算法的搜索路径优化。因此,为了适用新的问题背景、改进解的质量,本文一方面提出新的假定结构方式,通过采用空间矩阵表征方式和新型算法编码控制装箱过程;另一方面提出三维装箱问题中大规模邻域搜索的关键元素选取方式,并以此优化传统启发式算法对装箱方案的搜索过程,避免陷入局部最优,从而快速有效地解决电商物流领域的3D-MBSBPP。
1. 问题描述及数学建模
本节对本文研究的3D-MBSBPP进行数学描述,并结合实际背景,对目标和约束进行介绍。
1.1 问题背景
多箱型三维装箱问题是指有多种不同的箱型,每种箱型有一个尺寸和成本,每种箱型的箱子可使用数量无限制,求能将给定三维物品集合内的所有物品全部装下且不存在物品空间重叠或超出箱子范围的总成本最小的箱子使用方案。而在本文研究的电商领域中,随着客户对便捷性需求的提高和企业对客户满意度的关注,单箱装载(将单个客户订单中所有物品装载至单个箱子中)逐渐成为物流企业在装箱中非常关注的一点。因此,本文所研究的问题,是一种以单箱装载为目标的3D-MBSBPP,具体是指基于客户订单和给定的多种可选箱型,确定一种箱型及其相应装箱方案,在尽可能单箱装载客户订单所有物品的基础上实现装载率最大;若出现无法单箱装载情况,则等效为多个在单箱装载更多物品的基础上实现装载率最大的多箱型三维装箱问题复合,其本质上与前文所述的在尽可能单箱装载所有物品的基础上实现装载率最大的要求相同,因此对于该情况本文不作过多赘述。
1.2 模型建立
1.2.1 相关参数
假设有
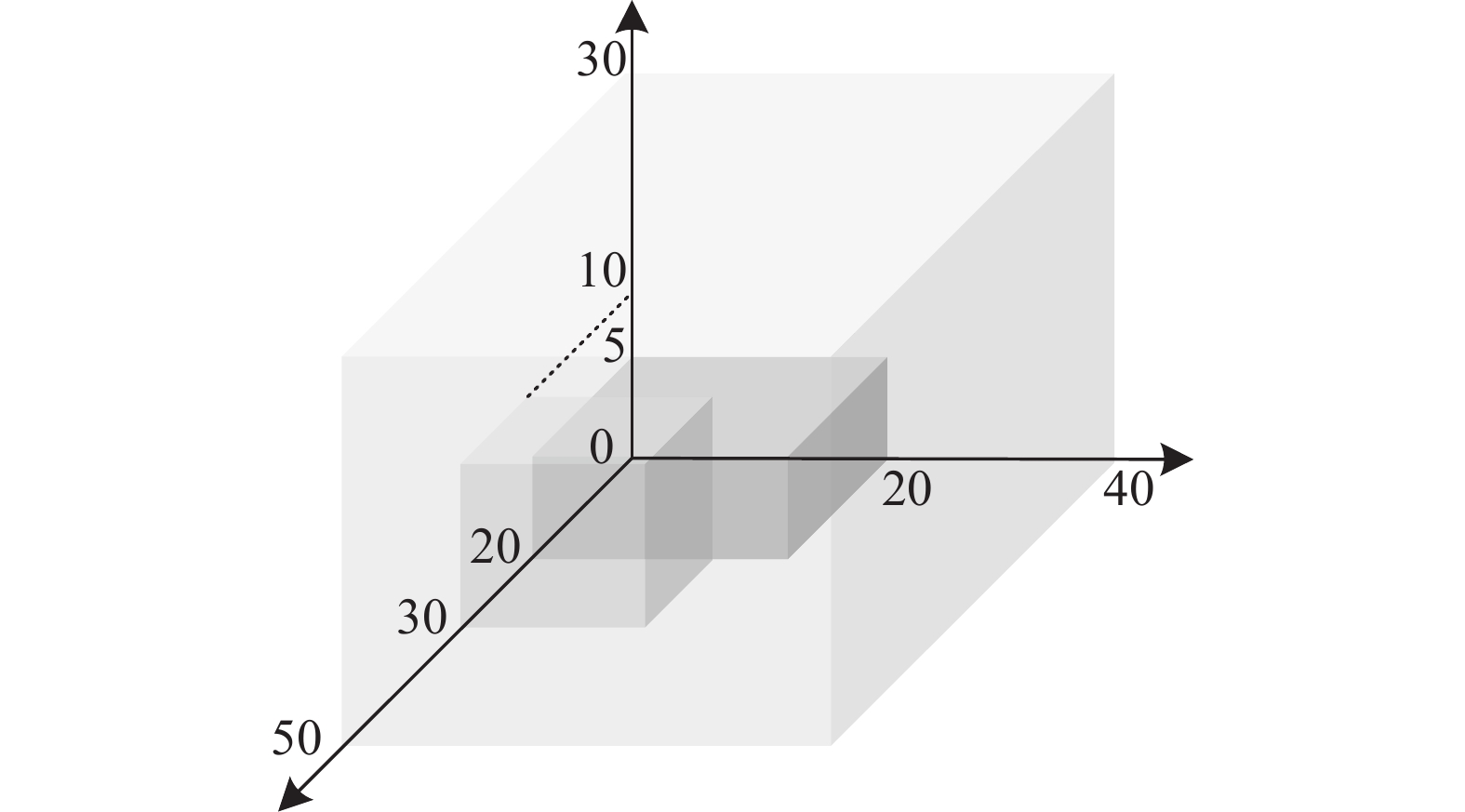
N 种给定的可选箱型,以有序集合(按箱子体积升序)B={b1,b2,⋯,bN} 表示,某客户订单中有n 个待装载物品,以有序集合(按物品体积降序)集合T={t1,t2,⋯,tn} 表示。其中,箱子bI 的长LI 、宽WI 、高HI ;物品ti 的长li 、宽wi 、高hi ,且LI⩾WI⩾HI ,lI⩾wI⩾hI 。I为被选箱型的编号,I=1,2,⋯,N ,i = 1,2,⋯,n 。同时,由于物品无摆放朝向约束,物品ti 在 X、Y、Z 轴上长度与长li 、宽wi 、高hi 的对应关系会因其不同朝向而变化,因此,定义lXi 、lYi 、lZi 分别表示其沿 X、Y、Z 轴上长度。问题目标是在满足给定装载约束的条件下,确定最优箱型及其相应的最优装箱方案。其中,最优箱型编号记为I *;最优装箱方案记为P*。因此,本文数学模型的决策变量为选用箱型编号I和对应装箱方案 P。
此外,为便于表示物品
ti 在箱子中的空间信息,作出如下参数设定。1) 物品ti 最靠近坐标原点的顶点以坐标(xi,yi,zi) 表示;2) 最远离坐标原点的顶点以坐标(x′i,y′i,z′i) 表示;3) 其在箱子中所占空间以(xi,yi,zi,xi+lXi,yi+lYi,zi+lZi) 形式表示,并记为ti 的空间信息。1.2.2 目标函数
由问题背景和求解目标可得本文所研究问题为多重优化问题,其中多重优化如下。
第1重优化 (所装物品数量最多)。
maxA=n∑i=1αi。 式中,
αi∈{0,1} ,i = 1,2,⋯,n ,根据装箱方案,若物品ti 装入当前被选箱子,αi = 1 ;若没有装入,则αi = 0 。第2重优化 (装载率最大)。
maxE=n∑i=1(αiliwihi)LIWIHI,I∈{1,2,⋯,N}。 由于第1重优化为主优化目标,上述两重优化目标函数可整合为单目标权重优化函数。
maxU(I,P)=ω1A+ω2E。 其中,
ω1、ω2 为各优化目标的权重系数,ω1,ω2∈[0,1] 。由于
A∈{0,1,⋯,n} ,E∈[0,1] ,根据二者数学关系,A对目标函数的影响远大于E。因此,上述两重优化目标函数可简化为maxU(I,P)=A+E。 1.2.3 数学模型
本文可行装箱方案必须满足如下两个条件:1) 任一装载的物品不能与其他装载物品或者箱子互相重叠;2) 所有装载的物品以与箱子平行的方式装载。
根据上述装箱约束条件和目标函数,建立如下数学模型。
maxU(I,P)=n∑i=1αi+n∑i=1αiliwihiLIWIHI。 (1) s.t.n∑i=1αiliwihi⩽LIWIHI; (2) x′i−xi=lXi,i=1,2,⋯,n; (3) y′i−yi=lYi,i=1,2,⋯,n; (4) z′i−zi=lZi,i=1,2,⋯,n; (5) sign(xi−xj)+sign(yi−yj)+sign(zi−zj)+sign(x′j−xi)+sign(y′j−yi)+sign(z′j−zi)<6,i,j=1,2,⋯,n; (6) sign(x′i−xj)+sign(y′i−yj)+sign(z′i−zj)+sign(x′j−x′i)+sign(y′j−y′i)+sign(z′j−z′i)<6,i,j=1,2,⋯,n; (7) xi∈[0,LI],yi∈[0,WI],zi∈[0,HI],i=1,2,⋯,n; (8) x′i∈[0,LI],y′i∈[0,WI],z′i∈[0,HI],i=1,2,⋯,n。 (9) 其中,
sign 为数学符号函数。上述约束中,式(1)为目标函数,目标为装载物品数量最多的基础上装载率最大;式(2)表示箱子最大容积约束;式(3) ~ (5)表示每个物品平行或正交装载于箱子内,由于当且仅当式(6)中6个符号函数之和为6时,物品
ti 近原点坐标(xi,yi,zi) 被另一物品包含;同理,式(7)是对物品ti 远原点坐标的约束,因此两式共同表示物品间不互相重叠;式(8) ~ (9)表示物品装载于箱子内。2. 算法设计
本文针对上述问题和数学模型,提出一种基于空间矩阵的大规模邻域搜索装箱算法,以便快速有效地求解问题。
在之前的三维装箱问题研究中,相关算法大多由基于结构假定方式的装箱检验算法和基于启发式规则的装箱方案路径搜索算法组成,并通过编码译码规则实现前者所得的解空间转化成后者所能处理的搜索空间。而本文则对上述算法进行创新,提出一种新的结构假定方式空间矩阵表征方式用于快速装箱检验,并提出基于物品朝向的编码译码规则以控制算法的迭代次数,最后通过定义关键元素选取方式,首次引入大规模邻域搜索算法以优化传统启发式算法对装箱序列的路径搜索过程。
2.1 空间矩阵表征方式
由于电商领域装箱订单具有个性化程度高特点,传统的结构假定方式不适用于电商问题背景;且由于三维装箱在空间布局中,干涉计算量较多,简单的坐标表示不利于问题求解。因此,本文首先提出空间矩阵表征方式用于装箱问题中的结构假定。Ngoi等[14]在夹具设计应用中提出一种基于可变正交单元的细胞分解、实体模型表征方式,本文则在其基础上提出应用于三维装箱问题中的空间矩阵表征方式,从而快速更新箱内空间使用情况,查找可用空间,便于装箱检验的模拟进行。空间矩阵外框架如图1所示。
2.1.1 相关介绍
空间矩阵将根据内部物品装箱情况分解成多个二维矩阵,每个二维矩阵表示某个高度范围内的箱内空间占用情况,具体表征方式如下。同时,由于空间矩阵中可用空间可视为由多个长方体组成,因此采用同上文物品
ti 空间信息一样的表述方式描述可用空间位置。步骤1 构建当前空间矩阵外框架。
1) 整理汇总X、Y、Z 轴参考量。根据所选箱子
bI 及其当前已装载物品ti ,将LI 及各物品的xi 、xi+lXi 汇总成 X 轴参考量,将WI 及各物品的yi 、yi+lYi 汇总成 Y 轴参考量,将HI 及各物品的zi 、zi+lZi 汇总成 Z 轴参考量。2) 对X、Y、Z 轴参考量进行去重和升序,并表示成
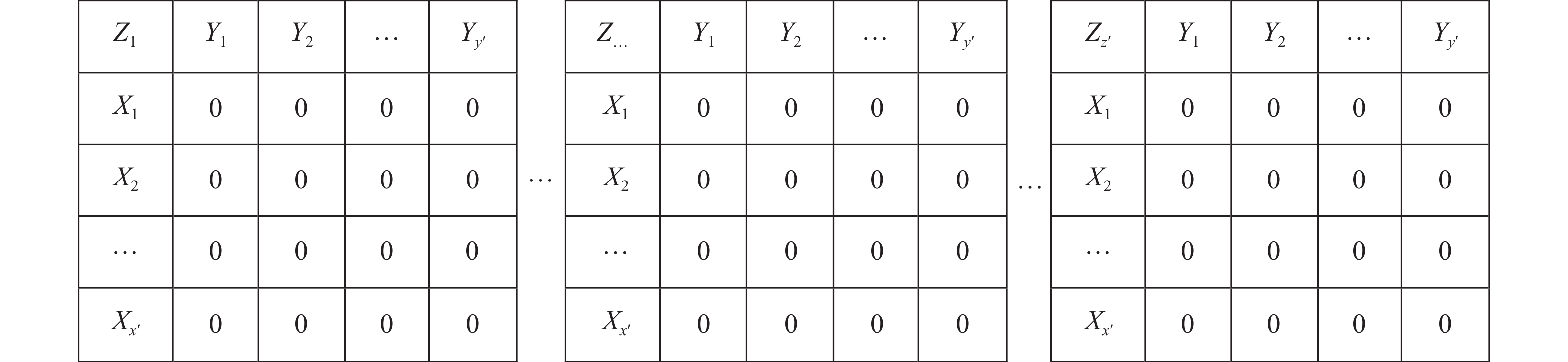
X′={X0,⋯,Xx′} ,Y′={Y0,⋯,Yy′} ,Z′={Z0,⋯,Zz′} ,其中,X0=Y0=Z0=0 ,x′ 、y′ 、z′ 与对应集合去重后的元素数量有关。3) 根据X、Y、Z 轴参考量生成如图1所示空间矩阵外框架,并填充0表示空间均无占用。
步骤2 确定每一层平面矩阵所包含物品。
1) Z 轴参考量分别对应各层平面矩阵层高。
2) 物品
ti 如满足条件zi<ZM⩽zi+lZi ,则其被第M层平面矩阵包含。步骤3 填充各层平面矩阵以表示空间占用情况。
1) 根据每层矩阵所包含的相应物品
ti ,确定其在相应平面矩阵的行起点、列起点、行终点、列终点,并填充1表示空间被占用。2) 确定行起点,若
xi=Xr,Xr∈X′ ,则其行起点为第r + 1行;确定列起点,若yi=Yr,Yr∈Y′ ,则其列起点为第r + 1列。3) 确定行终点,若
xi+lXi=Xs,Xs∈X′ ,则其行终点为第s 行;确定列终点,若yi+lYi=Ys,Ys∈Y′ ,则其行终点为第s 列。步骤4 寻找空间矩阵内可用空间。
1) 记空间矩阵第
x 行、第y 列、第z层元素为Fxyz ,其中,x=1,⋯,x′ ;y=1,⋯,y′ ;z=1,…,z′ 。2)
∀x∈{1,⋯,x′} ,y∈{1,⋯,y′} ,z∈{1,⋯,z′} ,若Fxyz=0 ,则有单位长方体子空间(Xx−1,Yy−1,Zz - 1,Xx,Yy,Zz) ,并记为sxyz 。3) 汇总可用单位长方体子空间,并基于预设规则将其合并为若干个较大的长方体子空间,组成可用空间集合
S ,其所含元素表示为S[p] ,p 表示装箱检验时,该子空间在集合中被选择的顺序,并定义其长宽高S[p]l⩾S[p]w⩾S[p]z ,在X、Y、Z轴上长度S[p]X 、S[p]Y 、S[p]Z 。装箱检验中,物品将按照集合中的顺序与可用空间逐一进行检验。2.1.2 使用示例
空间矩阵表征方式运用示例如下。当前空间矩阵内装箱情况如图2所示。已知
X′={0,20,30,50} ,Y′={0,10,20,40} ,Z′={0,5,10,30} 。构建空间矩阵外框架,并填充各层平面矩阵空间占用情况,得空间矩阵如图3所示。2.2 算法优化设计
2.2.1 编码规则
启发式算法在三维装箱问题中运用成功的关键在于通过编码规则将问题的可行解从其解空间转化到算法能处理的搜索空间[15]。在之前的三维装箱问题研究中,大多以有序物品集合作为编码方式,实现启发式算法的搜索空间和装箱方案可行解空间的相互转化。而本文为简化模型,便于搜索,提出一种新的算法编码,以有朝向约束的物品(简称物品(朝向))作为搜索空间,以有序的物品(朝向)集合作为可行解。
由于物品
ti 的可旋转性,lXi 、lYi 、lZi 会因摆放朝向的变化而改变。根据物品需平行或正交装载于箱子内的约束条件,物品有6种摆放朝向,故lXi 、lYi 、lZi 也有6种组合。因此,基于物品集合T={t1,t2,⋯,tn} 建立集合T′={1,2,⋯,6n} ,其中,T'的元素表示物品(朝向),ti 的6种朝向分别对应集合T'中的6i−5 至6i ,从而避免在后续算法中考虑物品的可旋转性。同时,构造函数i(t′)=(t′−1)//6+1 ,其中,//为整除符号;t′∈T′ ,i(t′) 表示物品(朝向)编号t′ 对应的物品编号。并定义物品每种摆放朝向下X、Y、Z 轴上长度与长宽高的对应关系,如式(10)所示,其中,%为取余符号。lXi(t′)={li(t′),t′%6=1,2;wi(t′),t′%6=3,4;hi(t′),t′%6=5,0。lYi(t′)={li(t′),t′%6=3,5;wi(t′),t′%6=0,1;hi(t′),t′%6=2,4。lZi(t′)={li(t′),t′%6=3,5;wi(t′),t′%6=0,1;hi(t′),t′%6=2,4。 (10) 预设装箱序列
Q 是一个过渡量,既是装箱方案路径搜索算法的输出量,也是装箱检验算法的输入量,表示算法根据启发式规则路径搜索出的未经过实际检验的预设装箱方案。Q 为一个包含n 个元素的有序集合,其第k 个元素表示为Q[k] ,表示在后续装箱检验的第k 阶段被检验能否装入箱子的物品(朝向)编号。为避免迭代次数超过装箱序列长度,预设序列Q 基于上述规则进行编码,Q[k]∈t ,从而通过避免在装箱过程中考虑物品旋转性以控制迭代次数,其中装箱检验由装箱算法实现。2.2.2 译码规则
在装箱方案路径搜索算法中,编码规则实现了问题的可行解从其解空间到算法能处理的搜索空间的转化,从而得出基于启发式规则搜索出的预设装箱序列
Q 。而在装箱检验算法中,则需要通过译码规则将Q 转化成空间矩阵可以模拟装载的各物品装箱顺序和朝向信息。译码规则如式(11)所示,首先将
Q[k] 译码成物品ti(Q[k]) 的lXi(Q[k]) 、lYi(Q[k]) 、lZi(Q[k]) 信息,再和当前空间矩阵Space 的可用空间SUB 进行装箱检验,并生成ti(Q[k]) 的xi(Q[k]) 、yi(Q[k]) 、zi(Q[k]) 信息,从而实现从预设装箱序列Q 到各物品实际空间信息的转换。lXi(Q[k])={li(Q[k]),Q[k]%6=1,2;wi(Q[k]),Q[k]%6=3,4;hi(Q[k]),Q[k]%6=5,0。lYi(Q[k])={li(Q[k]),Q[k]%6=3,5;wi(Q[k]),Q[k]%6=0,1;hi(Q[k]),Q[k]%6=2,4。lZi(Q[k])={li(Q[k]),Q[k]%6=0,4;wi(Q[k]),Q[k]%6=2,5;hi(Q[k]),Q[k]%6=1,3。 (11) Q 中各元素逐一译码并装箱检验后,求得该预设序列所对应的各物品空间信息。为便于后续启发式算法对装箱方案的迭代优化,对上述各物品空间信息再逐一编码生成实际装箱方案P 。P 是与Q 对应的包含n 个元素的有序集合,表示一种可行的装箱方案,其第k 个元素表示为P[k] 。P[k] 为实际装箱的第k 阶段中,实际装入箱子的物品(朝向)编号,其值可能会因为装箱检验的调整与Q[k] 不一致。2.2.3 大规模邻域搜索算法优化设计
本文在传统启发式算法搜索装箱方案的过程中,通过对关键元素选取和相关度函数定义,引入大规模邻域搜索算法。
1) 大规模邻域搜索算法关键元素选取和相关度函数定义。
分析目标函数
maxU(I,P)=A+E ,其中,E∈[0,1] ,故A的取值即箱子所装物品数对目标函数值起关键影响。因此,P中无法成功装箱的元素即为关键元素,关键元素集合表示为R={P[k]|P[k]<0,P[k]∈P} ,其第d 个元素记为R[d] ,R中元素数量记为D。2) 相关度函数定义。
根据本文问题背景,关键元素与装箱方案的相关度由其对应物品的体积大小决定,因此其相关度函数表示为
φ(R[d])=li(R[d])×wi(R[d])×hi(R[d]) 。同时,为简便计算,根据各关键元素相关度大小,筛选保留原集合R中部分相关度较高的关键元素,即R[1],⋯,R[⌈D3⌉] 。2.3 算法流程描述
2.3.1 子算法装箱检验算法
步骤1 初始化
k=1 ,输入预设装箱方案Q 和被选箱型I。步骤2 根据所选箱子
bI 构建空间矩阵。步骤3 根据当前所装物品信息及空间矩阵表征方式规则,更新空间矩阵及其可用空间集合
S 。步骤4 将
Q[k] 解码成物品ti(Q[k]) 的lXi(Q[k]) 、lYi(Q[k]) 、lZi(Q[k]) ,并将其解码信息与S 进行装箱检验,根据检验情况调整Q[k] 生成相应P[k] ,并确定ti(Q[k]) 的xi(Q[k]) 、yi(Q[k]) 、zi(Q[k]) 。1) 初始化
p=1 ,当前S 中所含子空间元素数量为s 。2) 根据物品
ti(Q[k]) 的尺寸信息,若S[p]l⩾li(Q[k]) 、S[p]w⩾wi(Q[k]) 、S[p]h⩾hi(Q[k]) ,则ti(Q[k]) 可装载于可用空间S[p] 中,否则p=p+1 ,跳至4)。3) 根据物品
ti(Q[k]) 的朝向信息,若物品可直接装箱,则P[k]=Q[k] ,若物品旋转后可装箱,则P[k]∈{6i(Q[k])−5,6i(Q[k])−4,⋯,6i(Q[k])} 。步骤4结束。4) 若
p⩽s ,返回2)。5) 物品
ti(Q[k]) 始终无法装箱,P[k]=−Q[k] ,负值表示物品ti(Q[k]) 在方案P 中无法装箱。步骤4结束。步骤5 如果
k<n ,n 为待装载物品数量,即未完成所有物品装箱检验,k=k+1 ,返回步骤3。步骤6 根据空间矩阵表征方式规则,获得空间矩阵当前所装物品信息,并输出实际装箱方案
P 和目标函数值U(I,P) ,算法结束。2.3.2 基于三维矩阵的大规模邻域搜索算法
步骤1 确定最小可用箱型编号I。
n∑i=1liwihi⩽LIWIHI,I∈{1,2,⋯,N}。 步骤2 启发式算法初始化,启发式迭代次数
m=0 。步骤3 根据蚁群算法信息素浓度规则生成
e 种预设装箱序列{Q1,Q2,⋯,Qe} 。步骤4 根据输入被选箱型I 和预设装箱序列
{Q1,Q2,⋯,Qe} ,调用装箱检验算法输出实际装箱方案{P1,P2,⋯,Pe} 和目标函数值{U1,U2,⋯,Ue} ,并确定该次迭代最优目标函数值U∗ 。U∗=max{U1,U2,⋯,Ue}。 步骤5 由于最优装箱方案可能并不唯一,根据
U∗ 生成最优装箱方案集合ˉP∗ 和其对应目标函数值集合ˉU∗ ,ˉP∗[j] 、ˉU∗[j] 分别表示其第j 个元素,J 为其所含元素数量。如果U∗>n ,则完成单箱装载所有物品,算法结束。1) 初始化
p=1 ,j=1 。2) 若
Up=U∗ ,则ˉP∗[j]=Pp ,ˉU∗[j]=U∗ 。3) 若
p<e ,则p=p+1 ,返回2),否则,确定集合ˉP∗ 和ˉU∗ 。4) 如果
U∗>n ,则I∗=I ,P∗∈ˉP∗ ,输出I∗ 和P∗ ,算法结束,否则步骤5结束,算法继续。步骤6 通过大规模邻域搜索算法优化集合
ˉP∗ 和相应目标函数值集合ˉU∗ 。1) 初始化
j=1 。2) 通过大规模邻域搜索算法优化装箱方案
ˉP∗[j] ,并初始化大规模邻域搜索迭代次数r=0 。3) 根据前文所述关键元素选取规则和相关度函数定义,确定并选取
ˉP∗[j] 中若干关键元素并计算各关键元素相关度,并保留部分相关度较高元素生成关键元素集合R。根据R中所保留关键元素,ˉP∗[j] 中相应元素依次与非关键元素随机置换重组。如果U(I,ˉP∗[j])>ˉU∗[j] ,则更新优化ˉP∗[j] 、ˉU∗[j] ,并转至4),否则,ˉP∗[j] 保持不变,跳至5)。4) 如果
ˉU∗[j]>n ,则I * = I,P∗=ˉP∗[j] ,输出I *和P*,算法结束,否则,算法继续。5) 如果
r 超过给定值或多次迭代没有新的ˉU∗[j] 产生,则当前装箱方案无大规模邻域搜索算法优化可能,转至6),否则,返回3),r=r+1 。6) 若
j<J ,则j=j+1 ,返回2),否则,更新最优目标函数值U∗=maxˉU∗ 及其对应最优装箱方案ˉP∗ ,步骤6结束。步骤7 根据启发式规则,强化最优装箱方案集合
ˉP∗ 对应路径信息素浓度。步骤8 如果
m 超过给定值或多次迭代没有新的U∗ 产生,则当前箱型限制下无更优方案,否则,返回步骤2,m=m+1 。步骤9 如果
I>N ,无更大箱型可以选择,则I∗=I ,输出I *和P*,算法结束,否则,返回步骤2,I =I+1 。3. 数值实验
本文的组合启发式算法以Python实现,程序试验运行在Intel Core i7-8750H 2.20 GHZ的处理器上。本文针对电商领域所提出的组合启发式算法,在电商领域3D-MBSBPP中具有良好表现。在实验中,为便于检验算法性能,本文组合启发算法的路径搜索算法部分拟采用蚁群算法作为大规模邻域搜索算法的优化对象,同时将基于电商领域物流装箱订单数据,与之前学者所提出的三维装箱算法、当前电商物流企业常用装箱软件进行性能比较。
3.1 算例说明
实验采用的标准算例集来自电商物流企业,共计49 591个客户订单和17种可选箱型,每个订单均可看作有17种箱型可选的3D-MBSBPP算例。此外,由于每个订单所含物品总体积小于最大箱型体积,且问题背景以单箱装载尽可能多物品为目标,因此装箱问题将以订单所含物品全部单箱装载成功作为达标情况并统计,从而简单直观地比较算法性能。
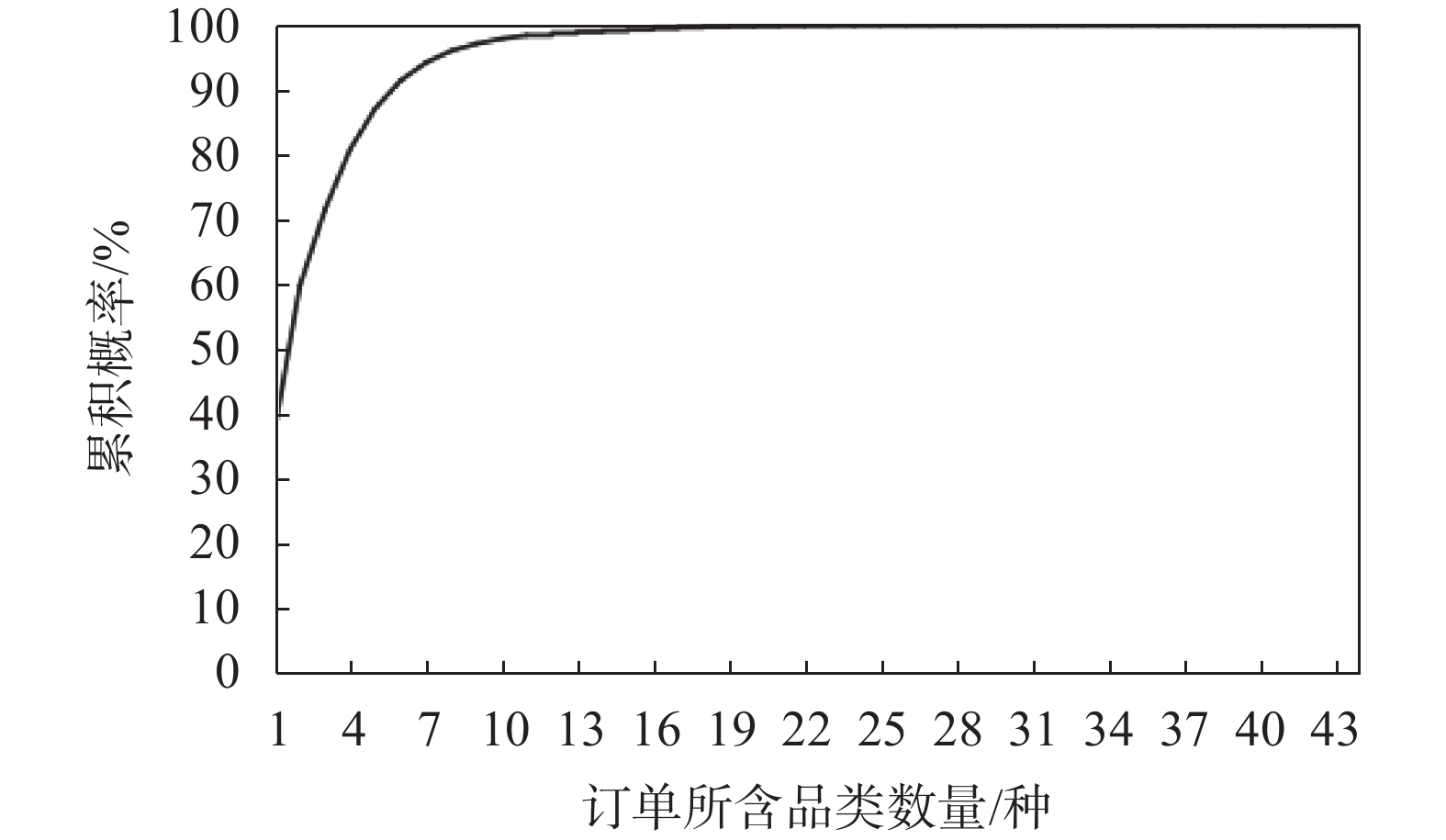
订单来自于电商物流企业实际订单,订单样本具有高度个性化特点,订单间品类数量波动大,订单所含品类最多达44种,所含物品数量最多达208个,品类数量概率分布如图4所示,物品数量概率分布如图5所示。箱型选择较多、长宽高比例特点明显,详细情况如表1所示。
表 1 箱型详细数据Table 1. Box type details箱型 长/cm 宽/cm 高/cm 体积/cm3 箱型 长/cm 宽/cm 高/cm 体积/cm3 1 2 12 6 1512 10 45 40 23 41400 2 2 15 14 4410 11 55 42 19 43890 3 3 18 10 5400 12 51 43 25 54825 4 3 18 15 8910 13 79 61 12 57828 5 3 26 15 11700 14 62 45 26 72540 6 4 30 12 16200 15 56 45 38 95760 7 3 25 20 17500 16 94 56 26 136864 8 4 30 25 30000 17 70 50 45 157500 9 4 36 18 31104 同时,为了便于比较本文算法和同类型装箱算法、商用软件在求解不同复杂程度的多箱型三维装箱问题时的性能,基于图4和图5,将算例集按照品类数量分成7组,详细情况如表2所示,按照物品数量分成9组,详细情况如表3所示。
表 2 标准算例集(按品类数量分组)Table 2. Standard example set (group by category quantity)组别 品类数量下限/种 品类数量上限/种 可选箱型种类/种 算例数量/个 1-1 1 2 17 29617 1-2 3 4 17 10477 1-3 5 6 17 5237 1-4 7 8 17 2277 1-5 9 10 17 928 1-6 11 44 17 1055 1-7 1 44 17 49591 表 3 标准算例集(按物品数量分组)Table 3. Standard example set (group by item quantity)组别 物品数量下限/个 物品数量上限/个 可选箱型种类/种 算例数量/个 2-1 1 2 17 23965 2-2 3 4 17 10159 2-3 5 6 17 6671 2-4 7 8 17 3845 2-5 9 10 17 1998 2-6 11 15 17 1852 2-7 16 30 17 1010 2-8 31 208 17 91 2-9 1 208 17 49591 此外,在上述的标准算例集中,虽然算例数量庞大,特点明显,但是其仅能实现本文算法和同类型装箱算法、商用软件的性能比较,无法实现和精确解的比较。因此,本文根据该电商物流企业的实际检验反馈,从49 591个标准算例中,遴选出其中58个算例作为特殊算例。这58个特殊算例虽然相较标准算例集,数量较少,但是经由人工装箱检验后理论精确解为100%(即所有装箱订单均可实现单箱全部装载),且当前该企业所有商用装箱软件均无法对其实现单箱全部装载,具有较大的比较价值。
3.2 比较实验
首先将基于前文分组后的标准算例集,分别进行本文算法和其他学者之前所提出的装箱算法、装箱软件的比较实验和结果分析,从而充分检验本文算法在求解不同品类数量复杂程度的3D-MBSBPP时的性能,比较结果如表4、表5所示。
表 4 与其他算法的结果比较(标准算例集)Table 4. Results compared with other algorithms (standard example set)组别 遗传算法[10] 模拟退火算法[11] 蚁群算法[12] 本文算法 速度/(s/单) 达标率/% 速度/(s/单) 达标率/% 速度/(s/单) 达标率/% 速度(s/单) 达标率/% 1-1 0.2554 84.24 0.8732 88.73 1.5704 88.75 1.6809 89.80 1-2 1.1044 81.72 1.7671 87.62 2.7577 87.80 2.7163 88.71 1-3 2.6024 76.82 3.4031 85.67 4.8079 86.13 4.6733 86.57 1-4 3.3790 76.98 3.8932 84.61 6.1815 85.22 4.8873 86.87 1-5 5.0219 74.87 5.2531 82.41 8.8046 83.34 6.0676 86.23 1-6 5.6293 70.28 7.3931 78.13 12.3458 79.81 8.2766 83.52 1-7 0.7075 82.15 1.6291 87.67 3.0925 87.83 2.5920 88.89 2-1 0.2488 85.77 0.4144 90.84 0.8991 90.93 0.9517 91.19 2-2 0.4967 82.92 1.0294 88.65 1.9185 88.79 1.8897 89.45 2-3 0.7621 79.67 1.9625 85.43 3.0552 85.61 2.8725 87.39 2-4 1.0113 77.04 2.6343 83.30 4.7384 83.54 3.7463 85.83 2-5 1.2959 73.57 3.4170 79.93 6.9003 80.28 4.7553 83.43 2-6 1.7219 70.41 4.9610 76.84 10.9563 77.21 6.6747 81.10 2-7 7.3264 64.95 16.1743 71.58 31.9576 72.08 24.6429 76.73 2-8 21.5359 60.44 53.8736 67.03 83.4827 68.13 68.4576 73.63 2-9 0.7075 82.15 1.6291 87.67 3.0925 87.83 2.5920 88.89 表 5 与商用软件的达标率比较(标准算例集)Table 5. Compliance rate compared with commercial softwares (standard example set) %组别 Eba-fit 装箱大师 本文算法 1-1 87.54 88.18 89.80 1-2 85.93 86.44 88.71 1-3 83.11 83.28 86.57 1-4 81.48 82.13 86.87 1-5 78.17 79.25 86.23 1-6 73.97 75.59 83.52 1-7 85.97 86.56 88.89 2-1 89.79 90.05 91.19 2-2 86.78 87.35 89.45 2-3 83.54 84.14 87.39 2-4 80.16 81.77 85.83 2-5 76.73 78.18 83.43 2-6 73.60 75.11 81.10 2-7 68.22 69.80 76.73 2-8 63.74 64.84 73.63 2-9 85.97 86.56 88.89 根据比较结果,在达标率方面,本文算法求解电商物流领域装箱问题时的性能优于其他算法和装箱软件,而且随着装箱问题复杂程度的提升,性能优势越发明显。此外,在求解速度方面,虽然本文算法慢于部分算法,但是同样随着装箱问题复杂程度的提升,求解速度的差距也在逐渐缩小。因此,本文算法相比之前针对弱异构性问题设计的算法、软件,能更好地满足高度个性化的电商物流邻域订单中强异构性和弱异构性兼有的要求。
最后,将基于特殊算例集对本文算法和其他装箱算法进行进一步性能比较,比较结果如表6所示。根据比较结果,本文算法达标率明显超过其他算法,充分体现出其性能的优越。而且,在求解商用软件无法解决而实际可解的装箱问题时,本文算法的达标率非常接近理论精确解100%,进一步证明本文算法对电商物流领域3D-MBSBPP的求解非常接近理论最优解。
4. 结论
本文提出一种针对个性化程度高的电商领域3D-MBSBPP的组合启发式算法。首先,根据电商物流背景建立数学模型;其次,以物品(朝向)作为算法搜索空间,建立编码译码规则及预设装箱序列、实际装箱方案等数据结构,并提出基于空间矩阵表征方式的装箱检验算法,快速实现从预设序列到实际方案的转换;最后,提出一种大规模邻域搜索算法,用于优化3D-MBSBPP中启发式算法的路径搜索过程。实验测试表明,本文所提出的组合启发式算法在求解电商物流3D-MBSBPP中,精度超过传统三维装箱算法,且运算速度较为理想。但是,本文所涉及的三维装箱问题约束较少,且大规模邻域搜索算法的重构规则较为简单,还需要进一步的调试参数、优化算法。
-
表 1 箱型详细数据
Table 1 Box type details
箱型 长/cm 宽/cm 高/cm 体积/cm3 箱型 长/cm 宽/cm 高/cm 体积/cm3 1 2 12 6 1512 10 45 40 23 41400 2 2 15 14 4410 11 55 42 19 43890 3 3 18 10 5400 12 51 43 25 54825 4 3 18 15 8910 13 79 61 12 57828 5 3 26 15 11700 14 62 45 26 72540 6 4 30 12 16200 15 56 45 38 95760 7 3 25 20 17500 16 94 56 26 136864 8 4 30 25 30000 17 70 50 45 157500 9 4 36 18 31104 表 2 标准算例集(按品类数量分组)
Table 2 Standard example set (group by category quantity)
组别 品类数量下限/种 品类数量上限/种 可选箱型种类/种 算例数量/个 1-1 1 2 17 29617 1-2 3 4 17 10477 1-3 5 6 17 5237 1-4 7 8 17 2277 1-5 9 10 17 928 1-6 11 44 17 1055 1-7 1 44 17 49591 表 3 标准算例集(按物品数量分组)
Table 3 Standard example set (group by item quantity)
组别 物品数量下限/个 物品数量上限/个 可选箱型种类/种 算例数量/个 2-1 1 2 17 23965 2-2 3 4 17 10159 2-3 5 6 17 6671 2-4 7 8 17 3845 2-5 9 10 17 1998 2-6 11 15 17 1852 2-7 16 30 17 1010 2-8 31 208 17 91 2-9 1 208 17 49591 表 4 与其他算法的结果比较(标准算例集)
Table 4 Results compared with other algorithms (standard example set)
组别 遗传算法[10] 模拟退火算法[11] 蚁群算法[12] 本文算法 速度/(s/单) 达标率/% 速度/(s/单) 达标率/% 速度/(s/单) 达标率/% 速度(s/单) 达标率/% 1-1 0.2554 84.24 0.8732 88.73 1.5704 88.75 1.6809 89.80 1-2 1.1044 81.72 1.7671 87.62 2.7577 87.80 2.7163 88.71 1-3 2.6024 76.82 3.4031 85.67 4.8079 86.13 4.6733 86.57 1-4 3.3790 76.98 3.8932 84.61 6.1815 85.22 4.8873 86.87 1-5 5.0219 74.87 5.2531 82.41 8.8046 83.34 6.0676 86.23 1-6 5.6293 70.28 7.3931 78.13 12.3458 79.81 8.2766 83.52 1-7 0.7075 82.15 1.6291 87.67 3.0925 87.83 2.5920 88.89 2-1 0.2488 85.77 0.4144 90.84 0.8991 90.93 0.9517 91.19 2-2 0.4967 82.92 1.0294 88.65 1.9185 88.79 1.8897 89.45 2-3 0.7621 79.67 1.9625 85.43 3.0552 85.61 2.8725 87.39 2-4 1.0113 77.04 2.6343 83.30 4.7384 83.54 3.7463 85.83 2-5 1.2959 73.57 3.4170 79.93 6.9003 80.28 4.7553 83.43 2-6 1.7219 70.41 4.9610 76.84 10.9563 77.21 6.6747 81.10 2-7 7.3264 64.95 16.1743 71.58 31.9576 72.08 24.6429 76.73 2-8 21.5359 60.44 53.8736 67.03 83.4827 68.13 68.4576 73.63 2-9 0.7075 82.15 1.6291 87.67 3.0925 87.83 2.5920 88.89 表 5 与商用软件的达标率比较(标准算例集)
Table 5 Compliance rate compared with commercial softwares (standard example set) %
组别 Eba-fit 装箱大师 本文算法 1-1 87.54 88.18 89.80 1-2 85.93 86.44 88.71 1-3 83.11 83.28 86.57 1-4 81.48 82.13 86.87 1-5 78.17 79.25 86.23 1-6 73.97 75.59 83.52 1-7 85.97 86.56 88.89 2-1 89.79 90.05 91.19 2-2 86.78 87.35 89.45 2-3 83.54 84.14 87.39 2-4 80.16 81.77 85.83 2-5 76.73 78.18 83.43 2-6 73.60 75.11 81.10 2-7 68.22 69.80 76.73 2-8 63.74 64.84 73.63 2-9 85.97 86.56 88.89 -
[1] TARANTILIS C D, ZACHARIADIS E E, KIRANOUDIS C T. A hybrid metaheuristic algorithm for the integrated vehicle routing and three-dimensional container-loading problem[J]. IEEE Transactions on Intelligent Transportation Systems, 2009, 10(2): 255-271. DOI: 10.1109/TITS.2009.2020187
[2] FANSLAU T, BORTFELDT A. A tree search algorithm for solving the container loading problem[J]. Informs Journal on Computing, 2010, 22(2): 222-235. DOI: 10.1287/ijoc.1090.0338
[3] CHE C H, HUANG W, LIM A, et al. The multiple container loading cost minimization problem[J]. European Journal of Operational Research, 2011, 214(3): 501-511. DOI: 10.1016/j.ejor.2011.04.017
[4] ELEY M. A bottleneck assignment approach to the multiple container loading problem[J]. Or Spectrum, 2003, 25(1): 45-60. DOI: 10.1007/s002910200113
[5] SULAIMAN H F, SARTANA B T, BUDIYANTO U. Genetic algorithm with random crossover and dynamic mutation on bin packing problem[C]. 2019 6th International Conference on Electrical Engineering, Computer Science and Informatics (EECSI). Bandung, Indonesia: IEEE, 2019: 229-234.
[6] FU Z Y, LV M G, WANG G Q, et al. The priority queue branch and bound method for multi-truck multi-container loading problem[J]. Modern Computer, 2019: 23-27.
[7] DELL'AMICO M, FURINI F, IORI M. A branch-and-price algorithm for the temporal bin packing problem[J]. Computers & Operations Research, 2020, 114: 104825.1-104825.16.
[8] LI X L, WANG J S, YANG X. Invasive weed optimization algorithm based on differential evolution operators to solve bin packing problem[C]. Proceedings of the 32th Chinese Control and Decision Conference 2020. Hefei: CCDC, 2020: 4141-4145.
[9] FAN Y, CHU J, XU H. Improvement grouping genetic algorithm for solving the bin packing problem[J]. Journal of Physics Conference Series, 2020, 1550: 032168. DOI: 10.1088/1742-6596/1550/3/032168
[10] 于明正, 徐斌, 陈佳. 基于双层启发式遗传算法的三维装箱问题[J]. 科学技术与工程, 2020, 20(5): 2042-2047. DOI: 10.3969/j.issn.1671-1815.2020.05.050 YU Mingzheng, XU Bin, CHEN Jia. 3D packing problem based on double-layer heuristic genetic algorithm[J]. Science Technology and Engineering, 2020, 20(5): 2042-2047. DOI: 10.3969/j.issn.1671-1815.2020.05.050
[11] 张钧, 贺可太. 求解三维装箱问题的混合遗传模拟退火算法[J]. 计算机工程与应用, 2019, 55(14): 32-39. ZHANG Jun, HE Ketai. Study on hybrid genetic and simulated annealing algorithm for three-dimensional packing problems[J]. Computer Engineering and Applications, 2019, 55(14): 32-39.
[12] 汪圆圆, 陈顺怀. 多目标蚁群算法在集装箱配载问题中的应用[J]. 武汉理工大学学报(交通科学与工程版), 2017(3): 479-483. WANG Yuanyuan, CHEN Shunhuai. Multi-objective ant colony algorithms for solving container loading plan problem[J]. Journal of Wuhan University of Technology (Transportation Science & Engineering), 2017(3): 479-483.
[13] 贾瑞玉, 马文华. 基于邻域搜索的改进最大最小蚁群算法[J]. 计算机仿真, 2014, 31(12): 261-264. DOI: 10.3969/j.issn.1006-9348.2014.12.058 JIA Ruiyu, MA Wenhua. The improved max min ant colony algorithm based on neighborhood search[J]. Computer Simulation, 2014, 31(12): 261-264. DOI: 10.3969/j.issn.1006-9348.2014.12.058
[14] NGOI B K A, WHYBREW K. A fast spatial representation method (applied to fixture design)[J]. The International Journal of Advanced Manufacturing Technology, 1993, 8(2): 71-77. DOI: 10.1007/BF01748770
[15] 庄凤庭, 张磊, 张春鲜, 等. 基于蚁群算法的集装箱装载问题[J]. 江南大学学报(自然科学版), 2007, 6(6): 795-799. ZHUANG Fengting, ZHANG Lei, ZHANG Chunxian, et al. Research on solution to container loading problem based on ant colony optimization[J]. Journal of Jiangnan University(Natural Science Edition), 2007, 6(6): 795-799.
-
期刊类型引用(5)
1. 肖茂友,范玉林,魏翔宇,唐沂媛. 考虑顾客订单分类与装卸顺序的三维装箱系统优化算法研究. 制造业自动化. 2025(03): 110-119 .  百度学术
百度学术
2. 徐翔斌,吁琴芳. 考虑作业姿势舒适的三维装箱问题. 工业工程. 2024(02): 37-47 .  本站查看
本站查看
3. 郭戈. 基于改进最小二乘支持向量机的电商细粒度数据采集检测研究. 自动化与仪器仪表. 2024(10): 69-74 .  百度学术
百度学术
4. 周冲,于兴林,杨静,林建瑞,林静,王张威. 一种基于经验数据和算法的物料包材推荐方法. 设备管理与维修. 2024(21): 43-46 .  百度学术
百度学术
5. 丁一芳,徐素秀,陆一平. 电子产品零部件的三维不规则堆叠优化问题研究. 物流技术. 2024(12): 70-84 .  百度学术
百度学术
其他类型引用(6)



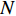
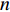
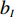
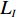
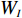
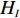
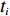
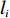
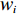
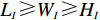
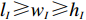
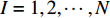
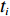
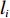
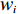
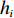
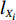
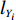
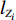
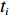
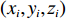
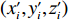
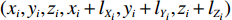
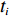
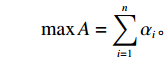
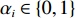
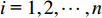
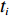
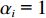
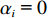
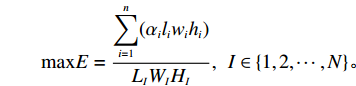
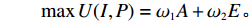
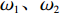
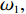
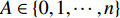
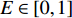
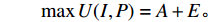
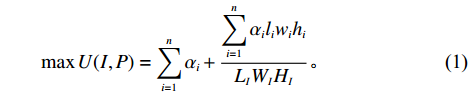
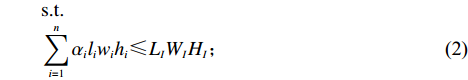
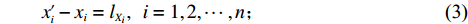
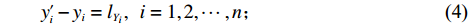
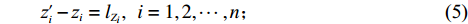
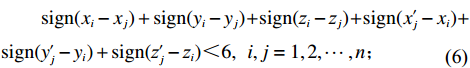
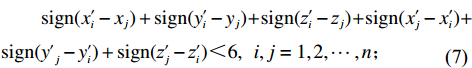
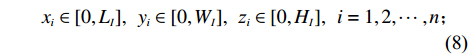
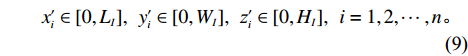
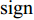
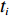
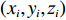
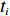
 下载:
下载: