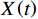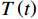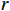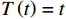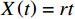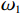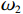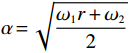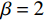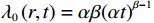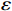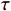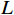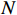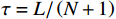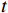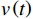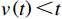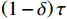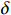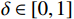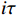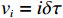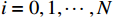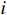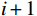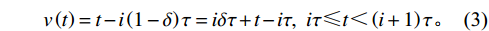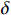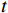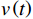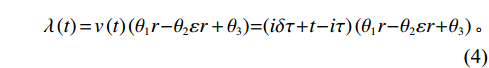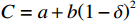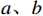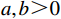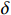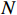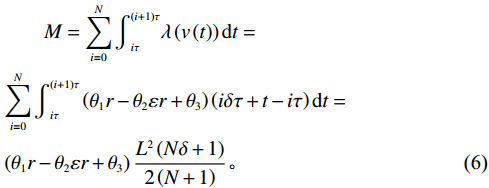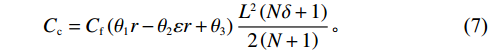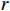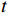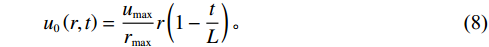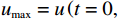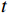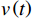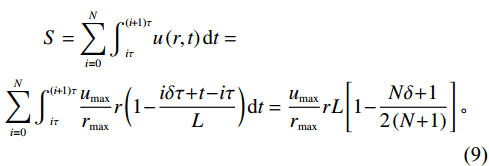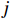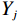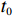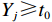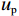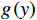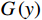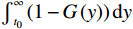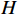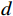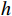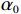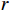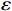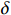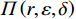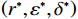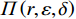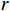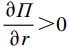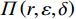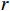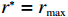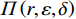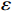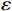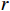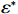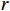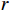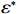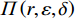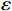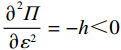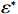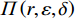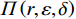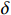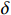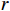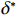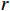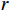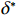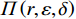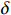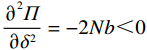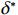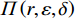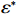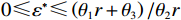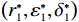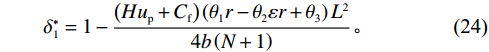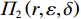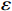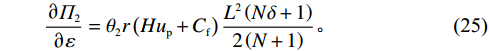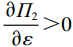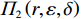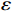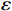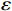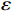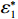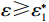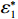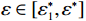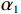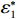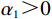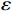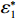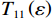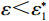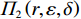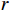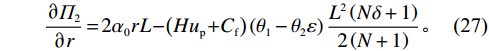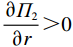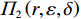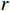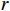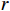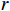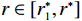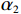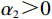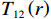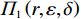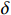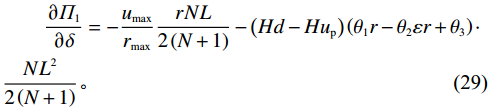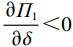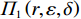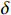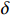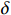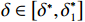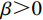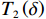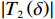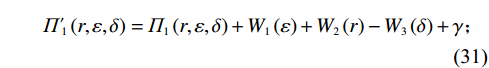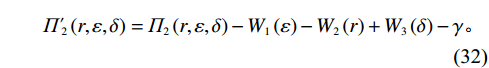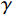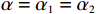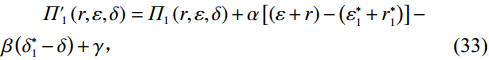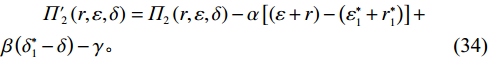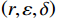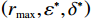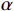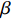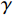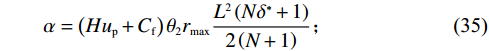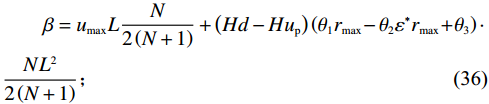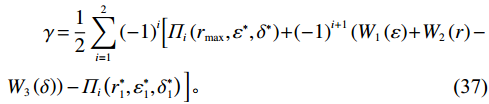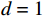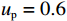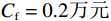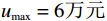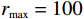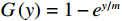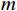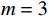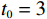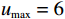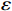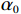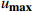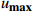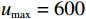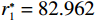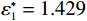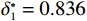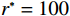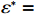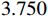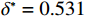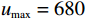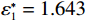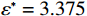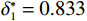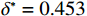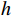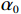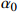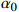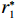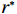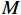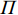Production Decisions and Revenue Adjustment Incentive Mechanisms in Leased Manufacturing Systems Considering Equipment Protection
-
摘要:
针对租赁设备合作生产过程中可能会出现承租方滥用设备的现象,提出一种考虑设备保护的租赁制造系统生产决策模型与收益调整激励机制,以形成租赁制造的最优生产策略。从设备保护的角度出发,构建考虑承租方对租赁设备使用率和保护程度的优化模型,以租赁制造系统总收益最大化为目标,确定设备保护的努力程度、设备使用率以及维护后设备状态与如新状态偏差度,即租赁制造系统的最优生产策略。提出一套收益调整激励机制,运用补偿金对合作双方的收益进行调整,并令双方独立决策的最优策略与系统最优策略相同,得到最佳补偿金系数,从而确定收益调整方案。案例研究表明,系统决策模型存在使得总收益最大的最优努力程度和预防维护程度,且系统决策下的最大总收益总是高于独立决策下的最大总收益,提升承租方对设备保护的努力程度和出租方对设备的预防程度,可以减少租赁设备平均故障次数。
Abstract:To address the potential issue of lessees abusing equipment during cooperative production in leased manufacturing systems, a production decision-making model and an incentive mechanism of revenue adjustment are proposed considering equipment protection to develop the optimal production strategy. From the perspective of equipment protection, an optimization model is developed considering the usage rate and protection degree of the leased equipment by lessees with the objective of maximizing the total revenue of the leased manufacturing system. The model determines the optimal production strategy by defining the effort degree of equipment protection, the equipment usage rate and the state deviation between a new equipment and the equipment after maintenance. Then, an incentive mechanism about revenue adjustment is proposed using compensation to adjust the revenue of both parties. The mechanism ensures that the optimal strategy for independent decision of each party align with the systematic optimal strategy. In this way, the best compensation coefficient is determined and the revenue adjustment plan is developed. Case study shows that the system decision-making model identifies the optimal effort degree and preventive maintenance degree that maximize the total revenue. Additionally, the maximum total revenue obtained by the system decision model is always higher than that with independent decisions. Moreover, increasing lessee efforts in equipment protection and lessor preventive maintenance can reduce the average number of failures of leased equipment.
-
随着时代的演进,科技不断进步,工业设备变得越来越复杂,而机械设备的价格也水涨船高。为了规避昂贵的购买和维护设备费用,越来越多的企业选择租赁设备而非购买。由于租赁设备的所有权属于出租方,承租方在使用过程中通常会忽视对设备的保护,导致在租赁期间设备故障频繁发生。与此同时,出租方负责设备的维护,希望通过制定合理的维护策略确保设备正常运行,并以较低的维护成本获取更高的收益,而这通常需要承租方的配合,即双方需要合作才能达到最佳的系统生产策略。为了实现系统层面的最佳生产策略,收益分配的激励机制也是不可或缺的。
1. 文献梳理
随着系统使用年限的不断增加,系统故障概率也会随之增加。因此,制定有效的维护策略以确保系统的正常运行是重要的。维护策略的制定需要考虑维护成本与设备故障成本之间的平衡,以确保维护策略的有效性。预防维护策略主要包括基于时间的维护、基于使用度的维护以及基于状态的维护。文献梳理如下。
1)基于时间的预防维护策略。金玉兰等[1]针对租赁设备维修时间的不确定性,建立考虑维修时间随机性的等周期预防性维护策略。Zhou等[2]提出租赁设备的定期预防性维护策略模型,该模型可以区分持续内部退化和随机外部冲击的影响。Chang等[3]提出以利润最大为目标的基于时间的控制限预防维修策略,系统役龄超过阈值时进行预防维修,还考虑了设备购买费和租赁结束时的设备剩余价值。文献[4-5]亦解决了不同问题场景的基于时间的预防维护策略问题。
2)基于使用度的预防维护策略。Hamidi等[6]建立两个非合作博弈论模型和一个合作博弈论模型,承租方决定租赁设备的使用率和租赁期,出租方确定租赁设备的维护策略。刘碧玉等[7]针对产品在租赁期达到前达到额定使用量,承租方需要延长租赁的情形,构建以出租方维修成本最小化为目标的预防维修决策模型,并通过算例分析确定最佳使用率范围。李龙辉等[8]考虑不同使用率顾客在二维质保结束时间和使用量上的差异性,构建基于二维质保期的需求模型和考虑周期预防性维护的质保成本模型,对基础质保时间和使用量限制、预防性维护次数和水平以及价格进行优化。Wang等[9]从出租人的角度出发,研究了在基于使用的连续租赁合同中考虑保修期的工业设备升级和预防性维护策略。
3)基于状态的预防维护策略。张云正等[10]研究基于状态检测的租赁设备的最优维修问题,建立以维修成本最低为目标的模型,确定系统最优的检测间隔和预防维修阈值。吴常洁等[11]建立面向动态租赁的双因子修复非新模型, 提出阶段租赁期内基于设备状态与特定环境的弹性预防维护策略。李亚平等[12-13]先后提出改进的转移概率矩阵描述外部冲击对退化的影响,构建预防维护策略的收益模型。此外,关于合作维护多主体间利益的研究也有很多研究成果。例如,Zhang等[14]提出一个分析模型来确定最优检查周期和预防维护阈值,以最大化出租方的利润。董克等[15]综合考虑设备的休眠期和预防维护等因素对维护费用的影响,从出租方角度出发,建立以维护总费用最小化为目标的周期预防维护模型。Huang等[16]考虑定制租赁服务,并为租赁行业开发了一个定价模型,提供定制的租赁合同以提高承租人购买租赁服务的意愿,从而增加出租人的总利润。
上述文献主要侧重于平衡出租方的惩罚成本和维护成本,以制定租赁设备的最佳预防维护策略,但很少考虑设备保护对预防维护策略的影响,而设备保护可以保障系统可靠性与稳定性。对于租赁设备老化问题的研究多集中于使用时间对设备的影响,忽视了承租方在租赁期间实际使用率对设备老化的影响。在实际情况中,租赁设备的故障常常受到使用时间和使用率的双重影响。
租赁制造系统的生产决策是一个复杂的问题,需要协调和平衡双方的利益。在这个过程中,合作才能够实现最优的生产策略,从而实现系统总收益最大化。而设备保护是合作过程中的重要环节,可以降低设备故障概率,有效提高制造系统的生产效率和经济效益,从而增强合作双方之间共赢意识,有利于合作的达成。激励机制在合作过程中起着至关重要的作用。合理的收益调整能够激励合作双方愿意合作,使得系统实现生产策略最优、总收益最大,并且双方能够从增加的系统收益中得到补偿,从而实现双赢的局面。
基于上述考虑,本文主要探讨设备保护和收益调整机制对租赁制造系统中生产决策的影响,主要创新点如下。
1)建立考虑设备保护和使用率的故障率函数模型,进而构建生产决策优化模型,求解得到租赁制造系统的最优生产策略。
2)为了实现系统最优策略,提出收益调整激励机制。激励机制主要考虑承租方(出租方)对出租方(承租方)的补偿金,即一方为了达到系统最优策略,对自身策略作出相应调整。这可能导致自身收益减少而对方收益增加(增加量大于减少量)的情形。这时,另一方就需要向其支付一定的补偿金,以激励对方进行合作,从而达到系统策略最优的目标。通过构建收益调整机制,即构建考虑补偿金的独立决策收益函数,令其最优解与系统决策下的最优解一致,得到补偿金系数(单位调整量的补偿金),从而确定合作中具体的利益调整方案,促使合作达成。
2. 问题描述
本文以单个租赁设备为研究对象,考虑由出租方将一台新设备出租给承租方,在租赁期间,设备由出租方进行维护。假设租赁设备租赁周期为
$ L $ ,出租方在租赁期间对设备进行$ N $ 次预防性维护。出租方执行不完美预防维护策略,即维护后租赁设备不能被恢复到如新状态。事后维护采取小修方式,被设置一个维修时间阈值。若超过此阈值,则出租方需要向承租方支付超时罚金,预防维护时间则忽略不计。假设每次维护后的设备状态与如新状态的偏差度为$ \delta $ ,反映出租方实际维护水平,$ \delta $ 介于0和1之间。假设承租方在设备保护层面愿意付出努力,如定期清洁、定期上润滑油等,使得设备故障率有所降低,令承租方为保护租赁设备的努力程度为$ \varepsilon $ ,$ \varepsilon > 0 $ 。承租方使用设备的频率或设备工作强度(加工设备每天加工产品100套,运输卡车每天运输200 t),通过租赁设备使用率$ r $ 表示,且令设备最大使用率为$ {r}_{\mathrm{m}\mathrm{a}\mathrm{x}} $ 。为了鼓励承租方与出租方在追求自身利益的同时,也重视系统整体利益,在系统最优维护策略的基础上,合作双方共同制定并执行利益调整激励机制,促进合作顺利进行,达到系统最佳决策的目的。
本文模型主要变量及其符号如表1所示。
表 1 模型的主要变量Table 1. Variables in the model符号 说明 符号 说明 $ r $ 设备使用率 $ {u}_{\mathrm{p}} $ 事后维修超时的单位时间罚金 $ \varepsilon $ 承租方保护租赁设备的努力程度 $ h $ 单位努力成本 $ \delta $ 维护后的设备状态与如新状态的偏差度 $ d $ 单位时间内承租方的停机损失 $ N $ 租赁周期内设备预防维护的次数 $ S $ 承租方在租赁周期内的总生产收益 $ L $ 设备租赁周期 $ g\left (y\right) $ 事后维修时间的概率密度函数 $ \tau $ 预防维护时间间隔 $ G\left (y\right) $ 事后维修时间的累积分布函数 $ {C}_{\mathrm{p}} $ 预防维护总成本 $ {\theta }_{1} $ 设备使用率对故障率的影响系数 $ {C}_{\mathrm{f}} $ 每次事后维修的固定成本 $ {\theta }_{2} $ 承租方努力程度对故障率的影响系数 $ {C}_{{\mathrm{c}}} $ 事后维修总成本 $ {\theta }_{3} $ 使用时间对故障率的影响系数 $ M $ 租赁期间设备平均故障次数 $ {\varPi }_{1} $ 承租方收益 $ {Y}_{j} $ 第$ j $次事后维修时间 $ {\varPi }_{2} $ 出租方收益 $ \lambda \left (t\right) $ 设备故障率函数 $ \varPi $ 系统总收益 $ v\left (t\right) $ 设备虚拟年龄 $ \alpha ,\beta ,\gamma $ 收益调整参数 $ {r}_{\mathrm{m}\mathrm{a}\mathrm{x}} $ 设备最大使用率 $ {\varPi }_{1}^{\mathrm{{'}}} $ 收益调整后承租方收益 $ {u}_{\mathrm{m}\mathrm{a}\mathrm{x}} $ 最大产能时单位时间产生的潜在收入 $ {\varPi }_{2}^{\mathrm{{'}}} $ 收益调整后出租方收益 3. 模型构建
3.1 故障率函数
设备故障率通常被设定为服从Weibull分布[17]。Hamidi等[6]认为设备故障率与设备使用率和运行时间有关系。设
$ X\left (t\right) $ 表示设备总使用量,$ T\left (t\right) $ 表示设备累计运行时间,$ r $ 表示设备使用率,反映承租方使用设备的频率或设备工作强度,例如,加工设备每天加工产品100套,运输卡车每天可运输200 t。在这种假设下,可以令$ T\left (t\right) =t $ ,$ X\left (t\right) =rt $ 。基于这些假设,设备故障率函数可以表示为$$\qquad {\lambda }_{0}\left (r,t\right) ={\omega }_{1}X\left (t\right) +{\omega }_{2}T\left (t\right) ={\omega }_{1}rt+{\omega }_{2}t 。 $$ (1) 其中,
$ {\omega }_{1} $ 表示使用率对故障率的影响系数;$ {\omega }_{2} $ 表示运行时间对故障率的影响系数。不难看出,式(1)是尺度参数$ \alpha = \sqrt{\dfrac{{\omega }_{1}r+{\omega }_{2}}{2}} $ ,形状参数$ \beta =2 $ 的Weibull分布函数的形式,即式(1)是$ {\lambda }_{0}\left (r,t\right) =\alpha \beta {\left (\alpha t\right) }^{\beta -1} $ 的一种特殊形式[6]。若承租方在租赁期间适度注意对设备的保护,例如定期清洁、定期上润滑油等,使得设备故障率有所降低,进而使得设备总使用量减少。令
$ \varepsilon $ 为承租方保护设备的努力程度,并将其被表示为设备总使用量的减少,那么,故障率函数可以表示为$$\qquad \lambda \left (r,t\right) =\left ({\theta }_{1}-{\theta }_{2}\varepsilon \right) rt+{\theta }_{3}t 。 $$ (2) 出租方在时刻
$ \tau 、2\tau 、\cdots 、N\tau $ 进行预防维护。其中,$ \tau $ 是两个连续预防维护操作之间的恒定时间间隔。令$ L $ 为设备租赁周期长度,$ N $ 为租赁周期内设备预防维护的次数,则预防维护时间间隔为$ \tau =L/\left (N+1\right) $ 。最后一次预防维护为替换更新。维护往往是不完美的,即维护后设备不能被恢复到如新状态。根据Kijima type-I模型[18],维护操作将设备从实际年龄
$ t $ 减少到虚拟年龄$ v\left (t\right) $ ,且$ v\left (t\right) < t $ 。该模型假设每次维护会将设备的年龄减少$ \left (1-\delta \right) \tau $ 。其中,$ \delta $ 为每次维护后的设备状态与如新状态的偏差度,反映出租方的维护水平,$ \delta \in \left[0,1\right] $ 。那么,在$ i\tau $ 时刻,执行维护操作后,设备的虚拟年龄为$ {v}_{i}=i\delta \tau $ ,$ i=\mathrm{0,1},\cdots , N $ 。这样,设备在第$ i $ 次和第$ i+1 $ 次预防维护操作之间的虚拟年龄可以表示为[18]$$\qquad v\left (t\right) =t-i\left (1-\delta \right) \tau =i\delta \tau +t-i\tau ,\;\; i\tau \leqslant t < \left (i+1\right) \tau 。 $$ (3) 不难看出,
$ \delta $ 越小,维护后设备虚拟年龄越小。将式(2)中的设备实际年龄
$ t $ 用式(3)中的虚拟年龄$ v\left (t\right) $ 代替,得到租赁设备故障率函数为$$ \begin{split} \qquad \lambda \left (t\right) = v\left (t\right) \left ({\theta }_{1}r - {\theta }_{2}\varepsilon r+{\theta }_{3}\right) = \left (i\delta \tau + t - i\tau \right) \left ({\theta }_{1}r - {\theta }_{2}\varepsilon r + {\theta }_{3}\right) 。 \end{split} $$ (4) 式(4)同时考虑了不完美维护效果与承租方对设备保护的努力程度。
3.2 成本与收益函数
1)维护成本。
每次预防维护成本为[19]
$ C=a+b{\left (1-\delta \right) }^{2} $ 。其中,$ a、b $ 分别表示每次维护的固定成本与可变成本,且$ a,b > 0 $ 。可以看出,$ \delta $ 越小,设备年龄减少量会越大,维护成本会越高。租赁周期内,$ N $ 次预防维护总成本为$$\qquad {C}_{\mathrm{p}}=Na+Nb{\left (1-\delta \right) }^{2} 。 $$ (5) 若设备在租赁期间发生故障,出租方对设备实施小修策略,使得设备恢复至如旧状态,即事后维修不改变设备故障率函数。因此,租赁期内设备的平均故障次数为
$$\begin{split} &\qquad M=\displaystyle\sum _{i=0}^{N}{\int }_{i\tau }^{\left (i+1\right) \tau }\lambda \left (v\left (t\right) \right) {\mathrm{d}}t=\\ &\displaystyle\sum _{i=0}^{N}{\int }_{i\tau }^{\left (i+1\right) \tau }\left ({\theta }_{1}r-{\theta }_{2}\varepsilon r+{\theta }_{3}\right) \left (i\delta \tau +t-i\tau \right) {\mathrm{d}}t=\\ & \left ({\theta }_{1}r-{\theta }_{2}\varepsilon r+{\theta }_{3}\right) \dfrac{{L}^{2}\left (N\delta +1\right) }{2\left (N+1\right) }\mathrm{。} \end{split} $$ (6) 假设每次事后维修都会产生固定成本
$ {C}_{\mathrm{f}} $ ,那么,租赁期间设备事后维修总成本可以表示为$$\qquad {C}_{\mathrm{c}}={C}_{\mathrm{f}}\left ({\theta }_{1}r-{\theta }_{2}\varepsilon r+{\theta }_{3}\right) \dfrac{{L}^{2}\left (N\delta +1\right) }{2\left (N+1\right) } 。 $$ (7) 2)承租方生产收益。
现实生产中,承租方对租赁设备的使用率越高,其产能就越大,单位时间的收入也就越高。然而,由于不完美预防维护的效果,设备故障率会随运行时间增加而增加,导致设备效率下降,进而导致收入减少。类似Cobb-Douglas生产函数,承租方收益率可以表示为关于
$ r $ 的递增函数和$ t $ 的递减函数[6],即$$\qquad {u}_{0}\left (r,t\right) =\dfrac{{u}_{\mathrm{m}\mathrm{a}\mathrm{x}}}{{r}_{\mathrm{m}\mathrm{a}\mathrm{x}}}r\left (1-\dfrac{t}{L}\right) \text{。} $$ (8) 其中,
$ {u}_{\mathrm{m}\mathrm{a}\mathrm{x}} $ 为设备在其产能被充分使用的情况下每单位时间产生的潜在收入,即$ {u}_{\mathrm{m}\mathrm{a}\mathrm{x}}=u\left (t=0, r={r}_{\mathrm{m}\mathrm{a}\mathrm{x}}\right) $ ;$ {r}_{\mathrm{m}\mathrm{a}\mathrm{x}} $ 为设备最大使用率。维护可以降低设备故障率,从而能够减少因设备劣化造成的收入损失。将式(8)中的年龄
$ t $ 替换为设备的虚拟年龄$ v\left (t\right) $ ,可以得到承租方在整个租赁周期内的总生产收益为$$\begin{split} &\qquad S=\displaystyle\sum _{i=0}^{N}{\int }_{i\tau }^{\left (i + 1\right) \tau }u\left (r,t\right) {\mathrm{d}}t=\\ & \displaystyle\sum _{i=0}^{N}{\int }_{i\tau }^{\left (i + 1\right) \tau }\dfrac{{u}_{\mathrm{m}\mathrm{a}\mathrm{x}}}{{r}_{\mathrm{m}\mathrm{a}\mathrm{x}}}r\left (1 - \dfrac{i\delta \tau + t - i\tau }{L}\right) {\mathrm{d}}t=\dfrac{{u}_{\mathrm{m}\mathrm{a}\mathrm{x}}}{{r}_{\mathrm{m}\mathrm{a}\mathrm{x}}}rL\left[1 - \dfrac{N\delta + 1}{2\left (N + 1\right) }\right]\mathrm{。} \end{split}$$ (9) 3)出租方超时罚金。
设备一旦因故障停止运行,将会导致承租方产生停机损失。为了减少停机损失,承租方希望事后维修时间越短越好。令第
$ j $ 次事后维修时间为$ {Y}_{j} $ ,事后维修阈值为$ {t}_{0} $ ,若$ {Y}_{j}\geqslant {t}_{0} $ ,意味着出租方事后维修任务超时,则出租方需要向承租方支付罚金。设$ {u}_{\mathrm{p}} $ 为出租方因为事后维修超时向承租方支付的单位时间的罚金,$ g\left (y\right) $ 和$ G\left (y\right) $ 分别是事后维修时间的概率密度函数和累积分布函数。那么,出租方需要向承租方支付的事后维修超时罚金可以表示为$$\begin{split} &\qquad P={u}_{\mathrm{p}}\displaystyle\sum _{j=1}^{M}\max\left (0,{Y}_{j}-{t}_{0}\right) ={u}_{\mathrm{p}}M{\int }_{{t}_{0}}^{\mathrm{\infty }}\left (y-{t}_{0}\right) g\left (y\right) {\mathrm{d}}y=\\ &{u}_{\mathrm{p}}M{\int }_{{t}_{0}}^{\mathrm{\infty }}\left (1-G\left (y\right) \right) {\mathrm{d}}y 。 \end{split} $$ (10) 4)承租方停机损失。
因为设备在运行过程中发生故障停机不可避免,因而本文仅考虑出租方维护超时导致承租方产生的停机损失。将式(10)中的
$ {\int }_{{t}_{0}}^{\mathrm{\infty }}\left (1-G\left (y\right) \right) {\mathrm{d}}y $ 记为$ H $ ,那么因出租方超时而导致的承租方停机损失为$$\qquad D=dMH 。 $$ (11) 其中,
$ d $ 为单位时间内承租方的停机损失。5)承租方保护设备的努力成本。
承租方对租赁设备进行保护,会产生努力成本。承租方保护设备的努力成本可以表示为[20]
$$\qquad E=\dfrac{1}{2}h{\varepsilon }^{2} 。 $$ (12) 其中,
$ h $ 是单位努力成本。6)承租方向出租方支付的租金。
承租方向出租方支付租金定义为
$$\qquad A={\alpha }_{0}{r}^{2}L 。 $$ (13) 其中,
$ {\alpha }_{0} $ 为价格系数,即承租方对租赁设备的使用率变动对租金的影响。根据上述分析的收益与成本函数,承租方的总收益函数可以表示为总生产收益与出租方超时罚金之和减去租金、努力成本与停机损失之和,即
$$\begin{split} &\qquad {\varPi }_{1}\left (r,\varepsilon ,\delta \right) =S+P-A-E-D=\\ & \dfrac{{u}_{\mathrm{m}\mathrm{a}\mathrm{x}}}{{r}_{\mathrm{m}\mathrm{a}\mathrm{x}}}rL\left[1-\dfrac{N\delta +1}{2\left (N+1\right) }\right]-{\alpha }_{0}{r}^{2}L-\dfrac{1}{2}h{\varepsilon }^{2} - \\ & \left (Hd-{Hu}_{\mathrm{p}}\right) \left ({\theta }_{1}r-{\theta }_{2}\varepsilon r+{\theta }_{3}\right) \dfrac{{L}^{2}\left (N\delta +1\right) }{2\left (N+1\right) } 。 \end{split} $$ (14) 出租方的总收益函数可以表示为租金减去预防维护成本、事后维护成本与维护超时罚金之和,即
$$\begin{split} &\qquad{\varPi }_{2}\left (r,\varepsilon ,\delta \right) =A-{C}_{\mathrm{p}}-{C}_{\mathrm{c}}-P={\alpha }_{0}{r}^{2}L-Na-\\ & Nb{\left (1-\delta \right) }^{2} -\left (H{u}_{\mathrm{p}}+{C}_{\mathrm{f}}\right) \left ({\theta }_{1}r-{\theta }_{2}\varepsilon r+{\theta }_{3}\right) \dfrac{{L}^{2}\left (N\delta +1\right) }{2\left (N+1\right) } 。 \end{split}$$ (15) 3.3 系统总收益及最优生产策略
出租方和承租方需要共同合作,才能实现租赁制造系统的最大效益。系统总收益函数可以表示为承租方总收益与出租方总收益之和,即
$$\begin{split} &\qquad \varPi \left (r,\varepsilon ,\delta \right) ={\varPi }_{1}\left (r,\varepsilon ,\delta \right) +{\varPi }_{2}\left (r,\varepsilon ,\delta \right) =\\ & \dfrac{{u}_{\mathrm{m}\mathrm{a}\mathrm{x}}}{{r}_{\mathrm{m}\mathrm{a}\mathrm{x}}}rL\left[1 - \dfrac{N\delta + 1}{2\left (N + 1\right) }\right] - Na-Nb{\left (1-\delta \right) }^{2} - \dfrac{1}{2}h{\varepsilon }^{2}- \\ &\left (Hd+{C}_{\mathrm{f}}\right) \left ({\theta }_{1}r-{\theta }_{2}\varepsilon r+{\theta }_{3}\right) \dfrac{{L}^{2}\left (N\delta +1\right) }{2\left (N+1\right) }。 \end{split} $$ (16) 以系统总收益最大化为目标,确定最优的设备使用率
$ r $ 、设备保护的努力程度$ \varepsilon $ ,以及维护后设备状态与如新状态偏差度$ \delta $ ,构成系统最优生产策略。具体来讲,通过求解$ \varPi \left (r,\varepsilon ,\delta \right) $ 关于各个决策变量的一阶偏导数,得到使得总收益最大的各个变量的最优解$ \left ({r}^{*},{\varepsilon }^{*},{\delta }^{*}\right) $ ,将最优解代入式(16)即可得到系统总收益。求解一阶偏导数的过程如下。$ \varPi \left (r,\varepsilon ,\delta \right) $ 对$ r $ 求一阶偏导数,得到$$\begin{split} &\qquad \dfrac{\partial \varPi }{\partial r}=\dfrac{{u}_{\mathrm{m}\mathrm{a}\mathrm{x}}}{{r}_{\mathrm{m}\mathrm{a}\mathrm{x}}}L\left[1-\dfrac{N\delta +1}{2\left (N+1\right) }\right]- \left (Hd+{C}_{\mathrm{f}}\right) \dfrac{{L}^{2}\left (N\delta +1\right) }{2\left (N+1\right) }\cdot \\ &\left ({\theta }_{1}-{\theta }_{1}\varepsilon \right)。 \end{split} $$ (17) 可以发现
$ \dfrac{\partial \varPi }{\partial r} > 0 $ ,式(17)显示$ \varPi \left (r,\varepsilon ,\delta \right) $ 是关于$ r $ 的递增函数。因此,在系统决策中,最优设备使用率等于其最大值$ {r}_{\mathrm{m}\mathrm{a}\mathrm{x}} $ ,即$ {r}^{*}={r}_{\mathrm{m}\mathrm{a}\mathrm{x}} $ 。令
$ \varPi \left (r,\varepsilon ,\delta \right) $ 对$ \varepsilon $ 的一阶偏导数为0,求解得到$ \varepsilon $ 最优值为$$\qquad {\varepsilon }^{\mathrm{*}}=\dfrac{\left (Hd+{C}_{\mathrm{f}}\right) {\theta }_{2}r{L}^{2}\left (N\delta +1\right) }{2h\left (N+1\right) } 。 $$ (18) 式(18)对
$ r $ 求一阶偏导数为$$\qquad \dfrac{\partial {\varepsilon }^{\mathrm{*}}}{\partial r}=\dfrac{\left (Hd+{C}_{\mathrm{f}}\right) {\theta }_{2}{L}^{2}\left (N\delta +1\right) }{2h\left (N+1\right) } > 0 。 $$ (19) 式(19)显示,
$ {\varepsilon }^{*} $ 是关于$ r $ 的递增函数,当$ r $ 取$ {r}_{\mathrm{m}\mathrm{a}\mathrm{x}} $ 时,$ {\varepsilon }^{*} $ 取得最大值。同时,$ \varPi \left (r,\varepsilon ,\delta \right) $ 关于$ \varepsilon $ 的二阶偏导数为$ \dfrac{{\partial }^{2}\varPi }{\partial {\varepsilon }^{2}}=-h < 0 $ 。因此,$ {\varepsilon }^{*} $ 是关于$ \varPi \left (r,\varepsilon ,\delta \right) $ 的极大值点。同理,令
$ \varPi \left (r,\varepsilon ,\delta \right) $ 关于$ \delta $ 的一阶偏导数为0,求解得到$ \delta $ 的最优值为$$\qquad {\delta }^{*} = 1 - \dfrac{{u}_{\mathrm{m}\mathrm{a}\mathrm{x}}rL+\left (Hd+{C}_{\mathrm{f}}\right) \left ({\theta }_{1}r-{\theta }_{2}\varepsilon r+{\theta }_{3}\right) {r}_{\mathrm{m}\mathrm{a}\mathrm{x}}{L}^{2}}{4b{r}_{\mathrm{m}\mathrm{a}\mathrm{x}}\left (N+1\right) } 。 $$ (20) 式(20)对
$ r $ 求一阶偏导数为$$\qquad \dfrac{\partial {\delta }^{*}}{\partial r}=-\dfrac{{u}_{\mathrm{m}\mathrm{a}\mathrm{x}}L+\left (Hd+{C}_{\mathrm{f}}\right) \left ({\theta }_{1}-{\theta }_{2}\varepsilon \right) {r}_{\mathrm{m}\mathrm{a}\mathrm{x}}{L}^{2}}{4b{r}_{\mathrm{m}\mathrm{a}\mathrm{x}}\left (N+1\right) } < 0\mathrm{。} $$ (21) 式(21)显示,
$ {\delta }^{*} $ 是关于$ r $ 的递减函数,当$ r $ 取$ {r}_{\mathrm{m}\mathrm{a}\mathrm{x}} $ 时,$ {\delta }^{*} $ 取得最小值。同时,$ \varPi \left (r,\varepsilon ,\delta \right) $ 关于$ \delta $ 的二阶偏导数为$ \dfrac{{\partial }^{2}\varPi }{\partial {\delta }^{2}}=-2Nb < 0 $ 。因此,$ {\delta }^{*} $ 是关于$ \varPi \left (r,\varepsilon ,\delta \right) $ 的极大值点。通过分析,可以得到设备保护的努力程度最优解
$ {\varepsilon }^{*} $ 的取值范围为$ 0\leqslant {\varepsilon }^{*}\leqslant \left ({\theta }_{1}r+{\theta }_{3}\right) /{\theta }_{2}r $ 。3.4 收益调整激励机制设计
由于系统最优策略不一定能够满足双方独立决策时的最优方案,因此,需要分析系统最佳方案与双方独立决策时各自的最佳方案,以确定合作中的收益再分配方案,从而促进合作的顺利实施。
通过最大化各自总收益函数,可以得到独立决策下最优解
$ \left ({r}_{1}^{\mathrm{*}},{\varepsilon }_{1}^{\mathrm{*}},{\delta }_{1}^{\mathrm{*}}\right) $ 。其中,$$\begin{split} &\qquad {r}_{1}^{\mathrm{*}}=\\ & \dfrac{\dfrac{{u}_{\mathrm{m}\mathrm{a}\mathrm{x}}}{{r}_{\mathrm{m}\mathrm{a}\mathrm{x}}}\left[1-\dfrac{N\delta +1}{2\left (N+1\right) }\right]-\left (Hd-H{u}_{\mathrm{p}}\right) \left ({\theta }_{1}-{\theta }_{2}\varepsilon \right) \dfrac{L\left (N\delta +1\right) }{2\left (N+1\right) }}{2{\alpha }_{0}} \text{;} \end{split}$$ (22) $$\qquad {\varepsilon }_{1}^{\mathrm{*}}=\dfrac{\left (Hd-H{u}_{\mathrm{p}}\right) {\theta }_{2}r{L}^{2}\left (N\delta +1\right) }{2h\left (N+1\right) } \text{;} $$ (23) $$\qquad {\delta }_{1}^{\mathrm{*}}=1-\dfrac{\left (H{u}_{\mathrm{p}}+{C}_{\mathrm{f}}\right) \left ({\theta }_{1}r-{\theta }_{2}\varepsilon r+{\theta }_{3}\right) {L}^{2}}{4b\left (N+1\right) } 。 $$ (24) 为了促进双方达成系统最优策略,提出一种收益调整激励机制。该激励机制主要是考虑承租方(出租方)对出租方(承租方)的补偿金,确保双方的收益都比独立决策时的收益更高,以此激励双方进行合作,从而达到系统最优策略。因此,本文讨论基于3个决策变量的收益调整问题。通过构建考虑补偿金的独立决策收益函数,最终得到补偿金系数(单位调整量的补偿金),从而确定具体的收益调整方案。
1)基于承租方保护设备努力程度的收益调整。
出租方总收益函数
$ {\varPi }_{2}\left (r,\varepsilon ,\delta \right) $ 关于$ \varepsilon $ 的一阶偏导数为$$\qquad \dfrac{\partial {\varPi }_{2}}{\partial \varepsilon }={\theta }_{2}r\left (H{u}_{\mathrm{p}}+{C}_{\mathrm{f}}\right) \dfrac{{L}^{2}\left (N\delta +1\right) }{2\left (N+1\right) } 。 $$ (25) 不难看出,
$ \dfrac{\partial {\varPi }_{2}}{\partial \varepsilon } > 0 $ ,$ {\varPi }_{2}\left (r,\varepsilon ,\delta \right) $ 是$ \varepsilon $ 的增函数,出租方的预期收益随着$ \varepsilon $ 的增加而增加。因此,出租方希望$ \varepsilon $ 越大越好。只有当$ \varepsilon $ 大于独立决策下的努力程度$ {\varepsilon }_{1}^{\mathrm{*}} $ 时,出租方才愿意向承租方支付补偿金。而$ \varepsilon \geqslant {\varepsilon }_{1}^{\mathrm{*}} $ 时,相较于$ {\varepsilon }_{1}^{\mathrm{*}} $ 的情况,承租方的收益会减少。从独立最优策略到系统最优策略,即$ \varepsilon \in [{\varepsilon }_{1}^{\mathrm{*}},{\varepsilon }^{*}] $ ,出租方需要支付给承租方的补偿金为$$\qquad {W}_{1}\left (\varepsilon \right) ={\alpha }_{1}\left (\varepsilon -{\varepsilon }_{1}^{\mathrm{*}}\right) 。 $$ (26) 其中,
$ {\alpha }_{1} $ 表示承租方将努力程度从$ {\varepsilon }_{1}^{\mathrm{*}} $ 增加一单位时出租方需要支付的补偿金,且$ {\alpha }_{1} > 0 $ 。如果承租方的努力程度$ \varepsilon $ 小于$ {\varepsilon }_{1}^{\mathrm{*}} $ ,则$ {T}_{11}\left (\varepsilon \right) $ 为负,表明较小的努力程度会使出租方需要承担更多的维修成本,承租方需要进行支付补偿金以弥补出租方的损失,因而,$ \varepsilon < {\varepsilon }_{1}^{\mathrm{*}} $ 这种情况在现实中不会发生。2)基于承租方单位时间设备使用率的收益调整。
出租方总收益函数
$ {\varPi }_{2}\left (r,\varepsilon ,\delta \right) $ 关于$ r $ 的一阶偏导数为$$\qquad \dfrac{\partial {\varPi }_{2}}{\partial r} = 2{\alpha }_{0}rL - \left (H{u}_{\mathrm{p}} + {C}_{\mathrm{f}}\right) \left ({\theta }_{1}-{\theta }_{2}\varepsilon \right) \dfrac{{L}^{2}\left (N\delta +1\right) }{2\left (N+1\right) } 。 $$ (27) 可以发现
$ \dfrac{\partial {\varPi }_{2}}{\partial r} > 0 $ ,那么,$ {\varPi }_{2}\left (r,\varepsilon ,\delta \right) $ 是关于$ r $ 的增函数,即出租方的预期收益随着$ r $ 的增加而增加,出租方希望$ r $ 越高越好。因此,在$ r $ 从独立最优策略到系统最优策略过程中,即$ r\in [{r}_{1}^{*},{r}^{*}] $ ,出租方需要向承租方支付的补偿金为$$\qquad {W}_{2}\left (r\right) ={\alpha }_{2}\left (r-{r}_{1}^{\mathrm{*}}\right) 。 $$ (28) 其中,
$ {\alpha }_{2} $ 表示当承租方将单位时间设备使用率增加一单位时出租方支付向其支付的金额,$ {\alpha }_{2} > 0 $ 。如果承租方降低使用率,则$ {T}_{12}\left (r\right) $ 为负,意味着承租方需要向出租方支付补偿金。然而,高使用率意味着设备发生故障的可能性增加,从而导致出租方维护成本增加。因此,在确定最优生产策略时,需要综合考虑单位时间设备使用率和维护成本。3)基于出租方维修后设备状态与如新状态偏差度的收益调整。
承租方总收益函数
$ {\varPi }_{1}\left (r,\varepsilon ,\delta \right) $ 关于$ \delta $ 的一阶偏导数为$$\begin{split} &\qquad \dfrac{\partial {\varPi }_{1}}{\partial \delta }=-\dfrac{{u}_{\mathrm{m}\mathrm{a}\mathrm{x}}}{{r}_{\mathrm{m}\mathrm{a}\mathrm{x}}}\dfrac{rNL}{2\left (N+1\right) }- \left (Hd-{Hu}_{\mathrm{p}}\right) \left ({\theta }_{1}r-{\theta }_{2}\varepsilon r+{\theta }_{3}\right)\cdot \\ &\dfrac{{NL}^{2}}{2\left (N+1\right) }。 \end{split} $$ (29) 不难看出,
$ \dfrac{\partial {\varPi }_{1}}{\partial \delta } < 0 $ ,$ {\varPi }_{1}\left (r,\varepsilon ,\delta \right) $ 是$ \delta $ 的减函数,承租方的预期收益随着$ \delta $ 减少而增加。因此,承租方鼓励出租方降低$ \delta $ 。只有当$ \delta \in \left[{{\delta }^{*},\delta }_{1}^{\mathrm{*}}\right] $ 时,承租方才愿意补偿出租方由此降低的收益。在偏差度从独立策略到系统最优策略变化过程中,承租方需要向出租方支付的补偿金为$$\qquad {W}_{3}\left (\delta \right) =\beta \left ({\delta }_{1}^{\mathrm{*}}-\delta \right) \text{。} $$ (30) 其中,参数
$ \beta > 0 $ 表示当出租方将偏差度减少一单位时承租方需要向其支付的金额。如果出租方增大偏差度,则$ {T}_{2}\left (\delta \right) $ 为负,出租方支付$ \left|{T}_{2}\left (\delta \right) \right| $ 金额以补偿承租方的收益损失。收益调整的目的是确保租赁双方更好的合作,收益调整后承租方和出租方的预期收益变为
$$\qquad {\varPi'}_{ 1}\left (r,\varepsilon ,\delta \right) ={\varPi }_{1}\left (r,\varepsilon ,\delta \right) +{W}_{1}\left (\varepsilon \right) +{W}_{2}\left (r\right) -{W}_{3}\left (\delta \right) +\gamma \text{;} $$ (31) $$\qquad {\varPi'}_{ 2}\left (r,\varepsilon ,\delta \right) ={\varPi }_{2}\left (r,\varepsilon ,\delta \right) -{W}_{1}\left (\varepsilon \right) -{W}_{2}\left (r\right) +{W}_{3}\left (\delta \right) -\gamma 。 $$ (32) 其中,
$ \gamma $ 是为了确保承租方和出租方通过调整获得的收益高于独立决策时的收益,从而鼓励双方进行系统决策。为简单起见,假设承租方对租赁设备的使用率和保护的努力程度对出租方的策略有着相同的影响,即
$ \alpha ={\alpha }_{1}={\alpha }_{2} $ 。从而,式(31)与(32)可以简化为$$\begin{split} &\qquad {\varPi'}_{ 1}\left (r,\varepsilon ,\delta \right) ={\varPi }_{1}\left (r,\varepsilon ,\delta \right) +\alpha \left[\left (\varepsilon +r\right) -\left ({\varepsilon }_{1}^{\mathrm{*}}+{r}_{1}^{\mathrm{*}}\right) \right]-\\ & \beta \left ({\delta }_{1}^{\mathrm{*}}-\delta \right) +\gamma \text{,} \end{split} $$ (33) $$\begin{split} & \qquad {\varPi'}_{ 2}\left (r,\varepsilon ,\delta \right) ={\varPi }_{2}\left (r,\varepsilon ,\delta \right) -\alpha \left[\left (\varepsilon +r\right) -\left ({\varepsilon }_{1}^{\mathrm{*}}+{r}_{1}^{\mathrm{*}}\right) \right]+\\ & \beta \left ({\delta }_{1}^{\mathrm{*}}-\delta \right) -\gamma 。 \end{split} $$ (34) 通过收益调整,独立决策下最优解
$ \left (r,\varepsilon ,\delta \right) $ 与系统决策下最优解$ \left ({r}_{\mathrm{m}\mathrm{a}\mathrm{x}},{\varepsilon }^{*},{\delta }^{*}\right) $ 相同,可以得到参数$ \alpha $ 、$ \beta $ 与$ \gamma $ 分别为$$\qquad \alpha =\left (H{u}_{\mathrm{p}}+{C}_{\mathrm{f}}\right) {\theta }_{2}{r}_{\mathrm{m}\mathrm{a}\mathrm{x}}\dfrac{{L}^{2}\left (N{\delta }^{*}+1\right) }{2\left (N+1\right) } \text{;} $$ (35) $$\begin{split} & \qquad \beta ={u}_{\mathrm{m}\mathrm{a}\mathrm{x}}L\dfrac{N}{2\left (N+1\right) }+ \left (Hd-H{u}_{\mathrm{p}}\right) \left ({\theta }_{1}{r}_{\mathrm{m}\mathrm{a}\mathrm{x}} -{\theta }_{2}{\varepsilon }^{\mathrm{*}}{r}_{\mathrm{m}\mathrm{a}\mathrm{x}} + {\theta }_{3}\right)\cdot\\ & \dfrac{N{L}^{2}}{2\left (N+1\right) } ; \end{split} $$ (36) $$\begin{split} & \qquad \gamma = \dfrac{1}{2}\sum _{i=1}^{2}{\left (-1\right) }^{i}\Big[{\varPi }_{i}\left ({r}_{\mathrm{m}\mathrm{a}\mathrm{x}},{\varepsilon }^{\mathrm{*}},{\delta }^{\mathrm{*}}\right) + {\left (-1\right) }^{i+1}\left ({W}_{1}\left (\varepsilon \right) + {W}_{2}\left (r\right) -\right. \\ & \left.{W}_{3}\left (\delta \right) \right) -{\varPi }_{i}\left ({r}_{1}^{\mathrm{*}},{\varepsilon }_{1}^{\mathrm{*}},{\delta }_{1}^{\mathrm{*}}\right) \Big] 。 \end{split} $$ (37) 4. 数值案例研究
以某租赁设备为研究对象,出租方将一台新设备出租给承租方,在租赁期间,设备由出租方进行维护,研究其生产策略与收益调整机制。出租方执行不完美预防维护策略,即维护后租赁设备不能被恢复到如新状态。此外,事后维护采取小修方式,被设置一个维修时间阈值,若超过此阈值,则出租方需要向承租方支付超时罚金,预防维护时间则忽略不计。承租方则会对设备执行定期清洁、定期上润滑油等保护动作。系统运行中的收益由总生产收益、租金、预防维护成本、事后维护成本、停机损失、努力成本和故障超时罚金构成。根据企业调研结果,模型相关参数初始值设置如下。设备保护的单位努力成本
$ h=1 $ 万元,单位停机损失$ d=1$ 万元,单位超时罚金$ {u}_{\mathrm{p}}=0.6 $ 万元,单次事后维修固定成本$ {C}_{\mathrm{f}}=0.2\mathrm{万}\mathrm{元} $ ,单位时间潜在收入$ {u}_{\mathrm{m}\mathrm{a}\mathrm{x}}=6\mathrm{万}\mathrm{元} $ ,设备最大使用率$ {r}_{\mathrm{m}\mathrm{a}\mathrm{x}}=100 $ t/月。假设事后维修时间服从指数分布,令其累积分布函数$ G\left (y\right) =1-{e}^{y/m} $ ,其中,$ m $ 为事后维修的平均时间,$ m=3 $ 。事后维修阈值$ {t}_{0}=3 $ 。假设设备的租赁周期为10个月,租赁期间,定期维护次数$ N=4 $ 。当承租方以最大使用率租用一个月,则需向出租方支付2万元,该设备给出租方带来的收入为6万元,即$ {u}_{\mathrm{m}\mathrm{a}\mathrm{x}}=6 $ 万元。基于以上数据,计算并讨论承租方和出租方合作下的系统决策与各自独立决策两种不同情形的生产策略。独立决策与系统决策下的收益情况及决策变量最优值(生产策略)结果如表2所示。从表2中可以看出,随着承租方保护设备的努力程度
$ \varepsilon $ 的提高,设备故障次数从14.983次减少到3.905次。这表明承租方的努力程度提高可以显著减少设备故障次数,一方面提高了设备的稳定性和可靠性,另一方面为决策双方带来更高的收益。因此,合作对系统总收益和参与者个人收益的增加具有显著积极的影响。表 2 独立决策与系统决策的生产策略与收益情况Table 2. Production strategies and revenue outcomes using independent and system decisions决策方式 $ {r}^{\mathrm{*}}_{1} $或$ {r}^{\mathrm{*}} $ $ {\varepsilon }^{\mathrm{*}}_{1} $或$ {\varepsilon }^{\mathrm{*}} $ $ {\delta }^{\mathrm{*}}_1 $或$ {\delta }^{\mathrm{*}} $ $ M $ $ \varPi $ $ {\varPi }_{1} $ $ {\varPi }_{2} $ 独立决策 82.962 1.420 0.826 14.983 761.380 757.870 3.510 系统决策 100 3.750 0.531 3.905 2170.000 1265.625 904.375 4.1 敏感性分析
分别对单位时间潜在收入
$ {u}_{\mathrm{m}\mathrm{a}\mathrm{x}} $ 、单位努力成本h、价格系数$ {\alpha }_{0} $ 作敏感性分析,研究3个参数的变化对决策变量、租赁期间平均故障次数以及收益等的影响。首先,单位时间潜在收入$ {u}_{\mathrm{m}\mathrm{a}\mathrm{x}} $ 敏感性分析结果如表3所示。表 3 单位时间潜在收入$ {\mathit{u}}_{\mathbf{m}\mathbf{a}\mathbf{x}} $ 敏感性分析结果Table 3. Sensitivity analysis of potential income$ {\mathit{u}}_{\mathbf{m}\mathbf{a}\mathbf{x}} $ per unit time决策方式 $ {u}_{\mathrm{m}\mathrm{a}\mathrm{x}} $ $ {r}^{\mathrm{*}}_1 $或$ {r}^{\mathrm{*}} $ $ {\varepsilon }^{\mathrm{*}}_1 $或$ {\varepsilon }^{\mathrm{*}} $ $ {\delta }^{\mathrm{*}}_1 $或$ {\delta }^{\mathrm{*}} $ $ M $ $ {\varPi }_{1} $ $ {\varPi }_{2} $ $ \varPi $ 独立决策 600 82.962 1.429 0.836 15.090 757.870 3.511 761.381 620 85.950 1.482 0.828 14.856 850.355 114.378 964.733 640 88.916 1.535 0.829 14.732 945.100 229.235 1174.335 660 91.869 1.589 0.831 14.605 1042.800 348.271 1391.071 680 94.804 1.643 0.833 14.462 1142.600 471.309 1614.909 系统决策 600 100 3.750 0.531 3.905 1265.625 904.375 2170.000 620 100 3.656 0.512 4.097 1478.760 829.521 2308.281 640 100 3.563 0.492 4.265 1694.624 753.399 2448.125 660 100 3.469 0.473 4.428 1913.525 676.006 2589.531 680 100 3.375 0.453 4.570 2135.156 597.344 2732.500 通过表3 可以计算得到,当单位时间产生的潜在收入增加到一定程度时,独立决策总收益占系统决策总收益的百分比由35.09%增加到56.13%,这是因为在合作模式下,承租方和出租方都会付出更多的努力去维护设备和提升效率,以减少设备故障发生次数,从而增加系统总收益。然而,当单位时间潜在收入增加到一定值时,所带来的收益将会边际递减。因此,合作对系统总收益的提升作用逐渐减弱。随着价格系数的增加,独立决策总收益占系统决策总收益的百分比由60.51%减少到35.09%。这是由于随着价格系数的增加,独立决策中承租方和出租方的收益均有所下降,从而导致系统总收益的下降。
通过表3发现,当
$ {u}_{\mathrm{m}\mathrm{a}\mathrm{x}}=600 $ 时,承租方在独立决策中对设备的使用率为$ {r}_{1}^{*}=82.962 $ ,保护设备的努力程度为$ {\varepsilon }_{1}^{*}=1.429 $ ,出租方对租赁设备维修后设备状态与如新状态的偏差度为$ {\delta }_{1}^{*}=0.836 $ 。如果参与者选择合作,承租方对租赁设备的最大使用率为$ {r}^{*}=100 $ ,此时,承租方保护设备的努力程度为$ {\varepsilon }^{*}= $ $ 3.750 $ ,出租方对租赁设备维修后设备状态与如新状态的偏差度为$ {\delta }^{*}=0.531 $ 。从独立决策到系统决策,承租方的收益从757.870增加到1265.625 ,出租方的收益从3.511增加到904.375。可以发现,选择合作可以为决策双方带来更大的收益提升。当$ {u}_{\mathrm{m}\mathrm{a}\mathrm{x}}=680 $ 时,如果承租方和出租方进行合作,承租方保护租赁设备的努力程度从$ {\varepsilon }_{1}^{*}=1.643 $ 增加到$ {\varepsilon }^{*}=3.375 $ ,出租方对租赁设备维修后设备状态与如新状态的偏差度将从$ {\delta }_{1}^{*}=0.833 $ 减少到$ {\delta }^{*}=0.453 $ 。从独立决策到系统决策,承租方的收益从1142.600 增加到2135.156 ,收益相对增加了87.0%;出租方的收益从471.309增加到597.344,收益仅增加了26.8%,总收益从1614.909 增加到2732.500 。单位努力成本
$ h $ 敏感性分析结果如表4所示。通过表4可以发现,随着单位努力成本的增加,承租方的收益随之增加,而出租方收益和系统总收益有所下降。这是由于单位努力成本的增加导致承租方保护设备的努力程度下降。然而,对于出租方而言,承租方保护设备的努力程度下降会导致设备故障次数增加,进而增加了维护成本,最终导致出租方的收益减少。在这种情况下,由于维护成本增加值超过了努力成本减少值,从而导致系统总收益的下降。因此,承租方应当积极通过技术改革或者管理手段降低单位努力成本,从而实现长期合作和共赢的局面。表 4 系统决策下单位努力成本h敏感性分析结果Table 4. Sensitivity analysis of unit effort cost h with system decisions$ h $ $ {r}^{\mathrm{*}} $ $ {\varepsilon }^{\mathrm{*}} $ $ {\delta }^{\mathrm{*}} $ $ M $ $ {\varPi }_{1} $ $ {\varPi }_{2} $ $ \varPi $ 100 100 3.750 0.531 3.906 1265.625 904.375 2170.000 105 100 3.478 0.511 4.631 1353.497 783.894 2137.391 110 100 3.243 0.493 5.223 1428.780 680.409 2109.189 115 100 3.038 0.478 5.712 1493.991 590.566 2084.557 120 100 2.857 0.464 6.122 1551.020 511.837 2062.857 价格系数
$ {\alpha }_{0} $ 敏感性分析结果如表5所示。通过表5可以发现,随着价格系数的增加,独立决策中承租方、出租方和系统总收益都出现显著的下降。当价格系数上升时,承租方对设备的使用率和保护设备的努力程度均有所下降,其中,承租方保护设备的努力成本减少值低于使用设备的生产收益减少值,从而导致承租方的收益减少。对于出租方而言,价格系数增加会导致设备使用率和租金减少,从而减少出租方的收益。需要注意的是,价格系数的变动对系统决策总收益的结果没有产生影响。这表明系统决策总收益独立于价格系数的变动,其决策结果更多地受到其他因素的影响。表 5 价格系数$ {\mathit{\alpha }}_{0} $ 敏感性分析结果Table 5. Sensitivity analysis of price coefficient$ {\mathit{\alpha }}_{0} $ 决策方式 $ {\alpha }_{0} $ $ {r}_{1}^{\mathrm{*}} $或$ {r}^{\mathrm{*}} $ $ {\varepsilon }_{1}^{\mathrm{*}} $或$ {\varepsilon }^{\mathrm{*}} $ $ {\delta }_{1}^{\mathrm{*}} $或$ {\delta }^{\mathrm{*}} $ M $ {\varPi }_{1} $ $ {\varPi }_{2} $ $ \varPi $ 独立决策 0.017 98.346 1.708 0.836 14.279 977.065 335.901 1312.966 0.018 92.652 1.603 0.832 14.576 897.528 208.916 1106.444 0.019 87.552 1.511 0.829 14.796 824.528 99.158 923.686 0.020 82.96 1.42 0.826 14.983 757.870 3.510 761.380 系统决策 0.017 100 3.750 0.531 3.905 1565.625 604.375 2170.000 0.018 100 3.750 0.531 3.905 1465.625 704.375 2170.000 0.019 100 3.750 0.531 3.905 1365.625 804.375 2170.000 0.020 100 3.750 0.531 3.905 1265.625 904.375 2170.000 4.2 对比分析
针对承租方考虑设备保护和不考虑设备保护两种情况,对系统最优策略时的设备使用率
$ {r}_{1}^{*} $ 或者$ {r}^{*} $ 、平均故障次数$ M $ 与系统总收益$ \varPi $ 作对比分析,分析结果如表6所示。表 6 对比分析结果Table 6. Results of comparative analysis行为方式 $ r/M/\varPi $ 独立决策 系统决策 不进行设备保护 $ {r}_{1}^{*} $或$ {r}^{*} $ 62.450 100 $ M $ 15 10 $ \varPi $ 147.428 1720.000 进行设备保护 $ {r}_{1}^{*} $或$ {r}^{*} $ 82.962 100 $ M $ 15 4 $ \varPi $ 761.381 2170.000 根据表6可以发现,如果承租方不对租赁设备进行保护,系统总收益显著低于进行设备保护行为下的系统总收益。同时在系统决策中,承租方进行设备保护行为可以显著降低设备故障次数。因此,考虑承租方对设备的保护行为具有一定的有效性和竞争性。
5. 结论
基于设备保护视角,建立考虑设备使用率和保护程度的租赁制造系统生产决策优化模型,以系统总收益最大化为目标,确定承租方设备保护的努力程度、设备使用率以及维护后设备状态与如新状态偏差度构成的系统最优生产策略。在此基础上,设计收益调整激励机制,旨在激励承租方与出租方进行合作,从而达到系统策略最优的目标。若承租方提高保护设备的努力程度,出租方需向其支付补偿金;若出租方预防维护程度提高,承租方需向其支付补偿金。
案例研究表明,系统最优策略模型存在使得总收益最大的最优努力程度和预防维护程度。而且,系统决策下的最大总收益总是高于独立决策下的最大总收益。敏感性分析表明,在租金较高或潜在收入较低的情况下,采用系统决策可以显著增加最优总收益,这意味着决策者可以根据具体情况选择合适的决策方案,实现最大化总收益的目标。此外,提升承租方对设备保护的努力程度和出租方对设备的预防程度,可以减少租赁设备平均故障次数,从而提高双方的收益。
-
表 1 模型的主要变量
Table 1 Variables in the model
符号 说明 符号 说明 r 设备使用率 up 事后维修超时的单位时间罚金 ε 承租方保护租赁设备的努力程度 h 单位努力成本 δ 维护后的设备状态与如新状态的偏差度 d 单位时间内承租方的停机损失 N 租赁周期内设备预防维护的次数 S 承租方在租赁周期内的总生产收益 L 设备租赁周期 g(y) 事后维修时间的概率密度函数 τ 预防维护时间间隔 G(y) 事后维修时间的累积分布函数 Cp 预防维护总成本 θ1 设备使用率对故障率的影响系数 Cf 每次事后维修的固定成本 θ2 承租方努力程度对故障率的影响系数 Cc 事后维修总成本 θ3 使用时间对故障率的影响系数 M 租赁期间设备平均故障次数 Π1 承租方收益 Yj 第j次事后维修时间 Π2 出租方收益 λ(t) 设备故障率函数 Π 系统总收益 v(t) 设备虚拟年龄 α,β,γ 收益调整参数 rmax 设备最大使用率 Π′1 收益调整后承租方收益 umax 最大产能时单位时间产生的潜在收入 Π′2 收益调整后出租方收益 表 2 独立决策与系统决策的生产策略与收益情况
Table 2 Production strategies and revenue outcomes using independent and system decisions
决策方式 r∗1或r∗ ε∗1或ε∗ δ∗1或δ∗ M Π Π1 Π2 独立决策 82.962 1.420 0.826 14.983 761.380 757.870 3.510 系统决策 100 3.750 0.531 3.905 2170.000 1265.625 904.375 表 3 单位时间潜在收入
umax 敏感性分析结果Table 3 Sensitivity analysis of potential income
umax per unit time决策方式 umax r∗1或r∗ ε∗1或ε∗ δ∗1或δ∗ M Π1 Π2 Π 独立决策 600 82.962 1.429 0.836 15.090 757.870 3.511 761.381 620 85.950 1.482 0.828 14.856 850.355 114.378 964.733 640 88.916 1.535 0.829 14.732 945.100 229.235 1174.335 660 91.869 1.589 0.831 14.605 1042.800 348.271 1391.071 680 94.804 1.643 0.833 14.462 1142.600 471.309 1614.909 系统决策 600 100 3.750 0.531 3.905 1265.625 904.375 2170.000 620 100 3.656 0.512 4.097 1478.760 829.521 2308.281 640 100 3.563 0.492 4.265 1694.624 753.399 2448.125 660 100 3.469 0.473 4.428 1913.525 676.006 2589.531 680 100 3.375 0.453 4.570 2135.156 597.344 2732.500 表 4 系统决策下单位努力成本h敏感性分析结果
Table 4 Sensitivity analysis of unit effort cost h with system decisions
h r∗ ε∗ δ∗ M Π1 Π2 Π 100 100 3.750 0.531 3.906 1265.625 904.375 2170.000 105 100 3.478 0.511 4.631 1353.497 783.894 2137.391 110 100 3.243 0.493 5.223 1428.780 680.409 2109.189 115 100 3.038 0.478 5.712 1493.991 590.566 2084.557 120 100 2.857 0.464 6.122 1551.020 511.837 2062.857 表 5 价格系数
α0 敏感性分析结果Table 5 Sensitivity analysis of price coefficient
α0 决策方式 α0 r∗1或r∗ ε∗1或ε∗ δ∗1或δ∗ M Π1 Π2 Π 独立决策 0.017 98.346 1.708 0.836 14.279 977.065 335.901 1312.966 0.018 92.652 1.603 0.832 14.576 897.528 208.916 1106.444 0.019 87.552 1.511 0.829 14.796 824.528 99.158 923.686 0.020 82.96 1.42 0.826 14.983 757.870 3.510 761.380 系统决策 0.017 100 3.750 0.531 3.905 1565.625 604.375 2170.000 0.018 100 3.750 0.531 3.905 1465.625 704.375 2170.000 0.019 100 3.750 0.531 3.905 1365.625 804.375 2170.000 0.020 100 3.750 0.531 3.905 1265.625 904.375 2170.000 表 6 对比分析结果
Table 6 Results of comparative analysis
行为方式 r/M/Π 独立决策 系统决策 不进行设备保护 r∗1或r∗ 62.450 100 M 15 10 Π 147.428 1720.000 进行设备保护 r∗1或r∗ 82.962 100 M 15 4 Π 761.381 2170.000 -
[1] 金玉兰, 刘莹, 严嘉欣. 考虑维修时间随机和维修惩罚的租赁设备预防性维护策略研究[J]. 工业工程与管理,2020,25(2):30-35. JIN Yulan, LIU Ying, YAN Jiaxin. Research on preventive maintenance strategy of leased equipment considering random maintenance time and maintenance penalty[J]. Industrial Engineering and Management, 2020, 25(2): 30-35.
[2] ZHOU X J, WU C J, LI Y T, et al. A preventive maintenance model for leased equipment subject to internal degradation and external shock damage[J]. Reliability Engineering & System Safety, 2016, 154: 1-7.
[3] CHANG W L, LO H C. Joint determination of lease period and preventive maintenance policy for leased equipment with residual value[J]. Computers & Industrial Engineering, 2011, 61(3): 489-496.
[4] XIA T, CAO L, XU Y, et al. Multi-level maintenance and inventory joint optimization for a k-out-of-n hyper-system considering the selection of suppliers with incentive discount policies[J]. Reliability Engineering & System Safety, 2024, 241: 109700.
[5] DE JONGE B, DIJKSTRA AS, ROMEIJNDERS W. Cost benefits of postponing time-based maintenance under lifetime distribution uncertainty[J]. Reliability Engineering & System Safety, 2015, 140: 15-21.
[6] HAMIDI M, LIAO HT, SZIDAROVSZKY F. Non-cooperative and cooperative game-theoretic models for usage-based lease contracts[J]. European Journal of Operational Research, 2016, 255(1): 163-174. DOI: 10.1016/j.ejor.2016.04.064
[7] 刘碧玉, 胡承阳, 杨海东. 二维租赁合同下考虑延长租赁基于可靠性的预防性维修决策[J]. 工业工程与管理,2023,28(4):38-46. LIU Biyu, HU Chengyang, YANG Haidong. Reliability-based preventive maintenance decision considering extended lease period in a two-dimensional lease contract[J]. Industrial Engineering and Management, 2023, 28(4): 38-46.
[8] 李龙辉, 刘子先, 张兆民, 等. 考虑预防性为维护的二维基础质保策略与价格联合优化[J]. 计算机集成制造系统,2023,29(11):3812-3822. LI Longhui, LIU Zixian, ZHANG Zhaomin, et al. Joint optimization of two-dimensional basic warranty strategy and price considering preventive maintenance[J]. Computer Integrated Manufacturing Systems, 2023, 29(11): 3812-3822.
[9] WANG XL, LI LS, XIE M. Optimal preventive maintenance strategy for leased equipment under successive usage-based contracts[J]. International Journal of Production Research, 2018, 157(18): 5705-5724.
[10] 张云正, 张晓红, 曾建潮. 租赁设备的状态维修决策建模与优化[J]. 系统工程理论与实践,2019(7):1732-1743. DOI: 10.12011/1000-6788-2017-2099-12 ZHANG Yunzheng, ZHANG Xiaohong, ZENG Jianchao. Modeling and optimization of state maintenance decision for leased equipment[J]. Systems Engineering Theory and Practice, 2019(7): 1732-1743. DOI: 10.12011/1000-6788-2017-2099-12
[11] 吴常洁, 滕春晓, 周晓军. 面向动态租赁的设备修复非新建模与弹性预防维护决策[J]. 计算机集成制造系统,2017,23(2):380-386. WU Changjie, TENG Chunxiao, ZHOU Xiaojun. Dynamic leasing oriented imperfect maintenance modeling and flexible preventive maintenance decision[J]. Computer Integrated Manufacturing Systems, 2017, 23(2): 380-386.
[12] 李亚平, 李海燕, 陶良彦. 基于 CSD-STM 的风电机马尔可夫链退化建模与预防维护策略[J/OL]. 计算机集成制造系统, 2022 (2022-11-03). https://kns.cnki.net/kcms/detail/11.5946.TP.20221103.1338.012.html. LI Yaping, LI Haiyan, TAO Liangyan. Reliability assessment and preventive maintenance strategy of wind turbine considering performance degradation and shocks[J/OL]. Computer Integrated Manufacturing Systems, 2022(2022-11-03). https://kns.cnki.net/kcms/detail/11.5946.TP.20221103.1338.012.html.
[13] 李海燕, 李亚平, 韩腾飞. 考虑自然退化与冲击的风电机可靠性评估与预防维护策略研究[J]. 工业工程,2023,26(3):67-74. LI Haiyan, LI Yaping, HAN Tengfei. A reliability assessment and preventive maintenance strategy of wind turbines considering natural degradation and shocks[J]. Industrial Engineering Journal, 2023, 26(3): 67-74.
[14] ZHANG Y Z, ZHANG X H, ZENG J C, et al. Lessees' satisfaction and optimal condition-based maintenance policy for leased system[J]. Reliability Engineering & System Safety, 2019, 191: 106519.
[15] 董克, 吕元芳. 考虑租赁延迟的设备预防维护策略优化研究[J]. 工业工程与管理,2016,21(1):60-66. DONG Ke, LYU Yuanfang. Optimal preventive maintenance policy for leased equipment considering lease delay[J]. Industrial Engineering and Management, 2016, 21(1): 60-66.
[16] HUANG Y S, HO J W, HUNG J W, et al. A customized warranty model by considering multi-usage levels for the leasing industry[J]. Reliability Engineering and System Safety, 2021, 215: 107769. DOI: 10.1016/j.ress.2021.107769
[17] LI Y, XIA T B, CHEN Z, et al. Multiple degradation-driven preventive maintenance policy for serial-parallel multi-station manufacturing systems[J]. Reliability Engineering & System Safety, 2023, 230: 108905.
[18] KIJIMA M. Some results for repairable systems with general repair[J]. Journal of Applied Probability, 1989, 26: 89-102. DOI: 10.2307/3214319
[19] PONGPECH J, MURTHY DNP, BOONDISKULCHOCK R. Maintenance strategies for used equipment under lease[J]. Journal of Quality in Maintenance Engineering, 2006, 12(1): 52-67. DOI: 10.1108/13552510610654538
[20] MA P, WANG H Y, SHANG J. Contract design for two-stage supply chain coordination: Integrating manufacturer-quality and retailer-marketing efforts[J]. International Journal of Production Economics, 2013, 146(2): 745-755. DOI: 10.1016/j.ijpe.2013.09.004
计量
- 文章访问数: 1180
- HTML全文浏览量: 36
- PDF下载量: 77



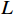
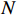
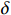
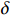
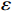
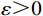
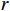

 下载:
下载: