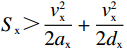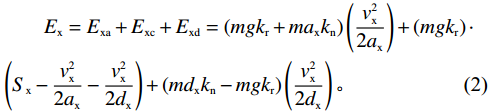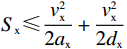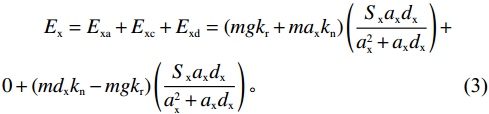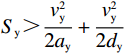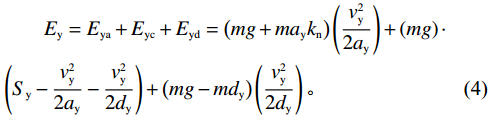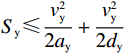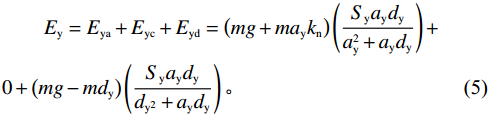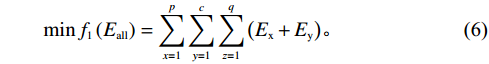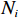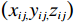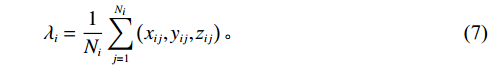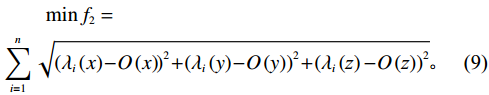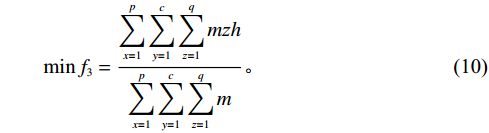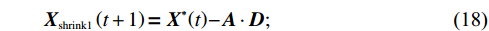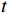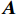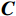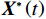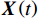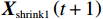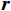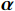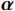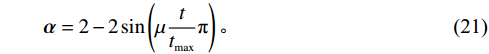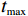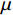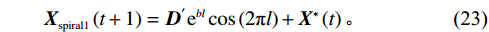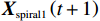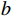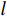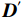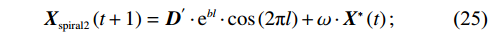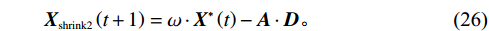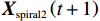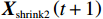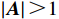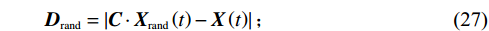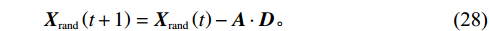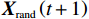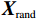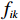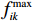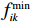Research on Multi-objective Storage Location Optimization in Automated Storage and Retrieval System Considering Energy Consumption
-
摘要:
针对自动化立体仓库货位分配问题,基于堆垛机运行路径、加速度以及产品类别等因素,建立了以降低堆垛机能耗、加强相关产品空间聚合、提高货架整体稳定性为优化目标的多目标优化模型。使用标准多目标鲸鱼优化算法(NSWOA)和改进的多目标鲸鱼优化算法(INSWOA)求解模型,借助Matlab对实际货物储位分配实例进行仿真验证,得出货位分配结果,对比分析结果证明了在解决货位优化问题时,所提出的模型及算法能够更好地改善自动化立体仓库作业过程能耗高、同类产品相关性低、货物摆放混乱的现状,有效解决自动化立体仓库货位分配问题。
-
关键词:
- 立体仓库 /
- 货位分配 /
- 多目标优化 /
- 鲸鱼优化算法(WOA)
Abstract:In addressing the inventory allocation problem in automated storage and retrieval systems (AS/RS), a multi-objective optimization model was established based on factors such as the operational path of the stacker crane, acceleration, and product categories. The objectives of this model are to reduce the energy consumption of the stacker crane, enhance the spatial aggregation of related products, and ensure the overall stability of the shelves. The standard multi-objective whale optimization algorithm (NSWOA) and an improved multi-objective whale optimization algorithm (INSWOA) were used to solve the model. Simulations were conducted using MATLAB on a real-world instance of inventory allocation, leading to specific allocation results. Comparative analysis proved that the proposed model and algorithms effectively improve the issues of high energy consumption, low correlation among similar products, and disorganized product placement in the operational processes of automated storage systems, thereby providing an effective solution to the inventory allocation problem in AS/RS environments.
-
在制造业智能化转型升级背景下,自动化立体仓库在现代物流仓储系统中取得广泛应用。其在提高仓库运营效率、节约人力成本、避免产品损坏等方面有显著优势。
自动化立体仓库中,货位合理分配对提高空间利用率和作业效率至关重要。国内外研究主要通过优化出入库效率、货品相关性、货架稳定性和巷道分布均衡来构建数学模型,以提升仓储运行效率[1-2]。如吴伟开等[3]建立了针对自动化立体仓库货位分配问题的数学模型,设计了改进的海鸥优化算法进行求解,并验证了该算法的有效性;李阳等[4]研究了航天零件仓储系统中的货位分配问题,运用模拟退火算法对模型进行求解;陈港生等[5]针对多巷道立体仓库中的货位分配问题,建立了多目标函数模型,并采用一种自适应多种群遗传算法进行求解;Jiao等[6]基于出入库操作时间、产品堆积程度和货架整体重心,构建了多目标数学模型,并提出了一种多种群遗传算法求解该数学模型;Yan等[7]针对电子产品在立体仓库存储时的货位分配问题,采用随机库存的动态货位分配策略,建立了多目标货位分配模型,采用改进的遗传算法进行求解;Wan等[8]基于高交付频率优先、相关性原则和大容量优先原则,建立了人工拣选区域的多目标货位优化模型,并采用遗传粒子群优化算法解决模型。
与此同时,在“绿色物流”“低碳物流”等概念的持续推动下,国内外开始关注自动化立体仓库中的能耗问题[9-10],主要集中在拣选路径优化、仓库布局和出入库作业调度等方面。例如,Ren等[11]从低碳经济的角度出发,研究SLP(systematic layout planning,系统设施布置)方法在减少仓库布局和运营过程中碳排放的理论潜力,并通过优化仓库内部设计和管理策略来实现仓库减碳的目标;方磊等[12]针对立库中能耗优化调度问题,建立了以最小化堆垛机任务总能耗为目标的调度模型,并通过改进的帝国竞争算法进行求解;夏绪辉等[13]针对立库中堆垛机在三维空间内的路径规划问题,综合考虑堆垛机运行时加速度、行走路径以及货物载重对能耗的影响,建立以最大化绿色度为目标的模型,并采用免疫蚁群算法进行求解。
综上所述,目前关于自动化立体仓库货位分配的研究主要集中在提高货架稳定性、提升货物出入库效率、巷道分布均衡等方面,对于堆垛机能耗优化方面研究较少,且现有研究多为单目标优化,与货位优化目标往往相互矛盾,因此,应采用多目标优化方法权衡最优解。本文在考虑堆垛机作业距离、运动特性和载货质量等因素的基础上,结合出入库效率和同类产品空间聚合因素,建立了考虑能耗的多目标自动化立体仓库货位优化模型,运用INSWOA (Improved multi-objective whale optimization algorithm, 改进的多目标鲸鱼优化算法) 算法求解,并通过实例仿真验证了该模型的适用性和算法的有效性。
1. 问题描述及相关假设
在家电制造业中,自动化立体仓库已经成为现代化生产的关键设施之一。由于家电产品种类繁多且多种配件之间相关性大,产品质量差异明显,不合理的货位分配会在运输过程中增加能耗。本文以某家电制造企业的自动化立体仓库为研究对象,探讨在保障堆垛机运行效率的同时如何合理分配货物的存储位置。
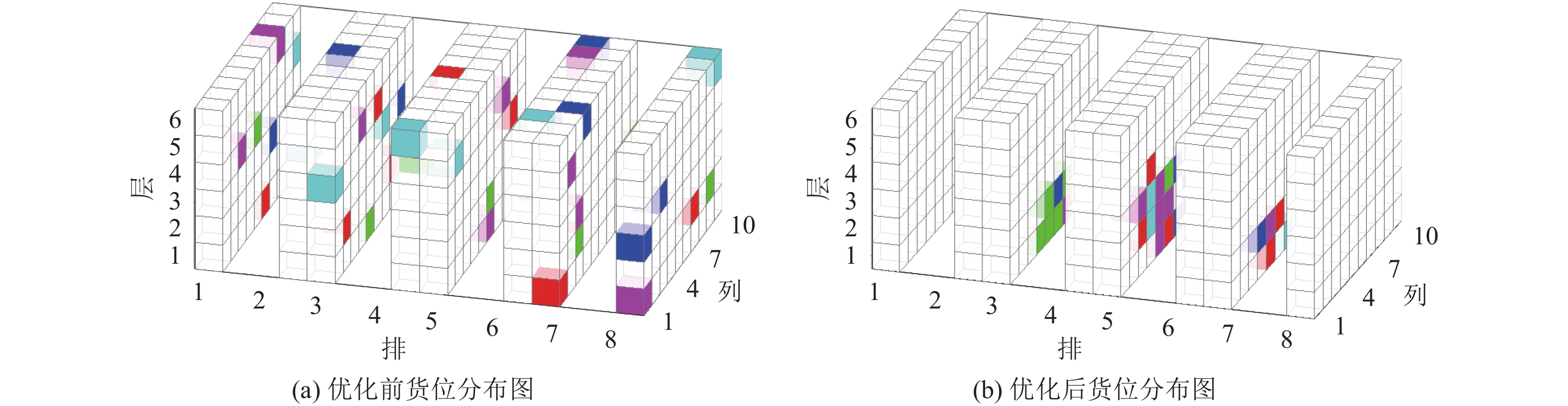
自动化立体仓库由多个巷道组成,并配备相应的自动化设备和系统来实现货物的存储、检索和搬运。主要包含高层货架系统、出入库台、堆垛机、输送系统、货物检测与识别系统。本文以某家电制造企业的立体仓库为研究对象,在该立体仓库中,每个巷道都配备了一台堆垛机,负责处理左右两侧货架上货物的存取任务,仓库布局如图1所示。
为求解自动化立体仓库的最优货位集合,满足作业能耗最低的同时兼顾货架重心以及相关产品空间聚合,对货位分配优化模型作如下假设:
1) 每个货位、货架的规格和最大承载都保持一致;
2) 自动化立体仓库内的I/O (input/output, 输入/输出)口在同一侧;
3) 将目标货位与出入口间的曼哈顿距离作为搬运距离;
4) 库内能存放的货位数大于等于入库货箱数;
5) 堆垛机启动、制动、转向和拣选时间均为固定值,这些固定值在计算中忽略不计;
6) 堆垛机每次只搬运一种货物;
7)考虑堆垛机的加速度;
8) 堆垛机完成任务后返回I/O点,穿梭车完成任务后回到等待点。
2. 构建货位优化模型
2.1 模型参数定义
本文模型参数定义如表1所示。
表 1 参数定义Table 1. Parameter definitions模型参数 定义 Ex/J 堆垛机水平运行时能耗 Exa/J 堆垛机在水平方向进行加速运动时能耗 Exc/J 堆垛机在水平方向进行匀速运动时能耗 Exd/J 堆垛机在水平方向进行减速运动时能耗 Ey/J 堆垛机垂直运行时能耗 Eya/J 堆垛机在垂直方向进行加速运动时能耗 Eyc/J 堆垛机在垂直方向进行匀速运动时能耗 Eyd/J 堆垛机在垂直方向进行减速运动时能耗 vx/ (m∙s−1) 堆垛机水平运行额定速度 vy/ (m∙s−1) 堆垛机垂直运行额定速度 g/ (m∙s−2) 重力加速度 kr 匀速状态下的滚动阻力系数 kn 非匀速状态下的转动质量阻力系数 ax/ (m∙s−2) 堆垛机水平运行加速度 dx/ (m∙s−2) 堆垛机水平运行减速度 ay/ (m∙s−2) 堆垛机垂直运行加速度 dy/ (m∙s−2) 堆垛机垂直运行减速度 p 货架的排数 c 货架的列数 q 货架的层数 L/m 单元货格的长度 w/m 单元货格的宽度 h/m 单元货格的高度 m/kg 货位为(x,y,z)的货物质量 o/m 全部货物的中心坐标 n 所有产品类别数 i 货物种类的索引,i∈[1,n] λi/m 货物种类i的平均中心坐标 Ni 第i类产品的个数,j∈[1,Ni] (xij,yij,zij)/m 种类i下第j个货物的坐标 2.2 降低堆垛机作业能耗模型
在家电制造业的仓库中,不同产品的质量差异明显,通过合理的货位分配可以优化货物的负载规划,使得运输的货物重量合理分配,减少电机的负荷,从而降低能耗。本文所研究的堆垛机在水平和垂直方向上运动,由各自电机提供驱动,且运动间相互独立,其运行能耗为水平及垂直方向所用能耗之和。
考虑到堆垛机在运动过程中会产生加速度,根据其运行速度是否能够达到额定速度,将运动形态分为两类。当运动路径长度大于临界值时,运输设备做第Ⅰ类运动,经历加速、匀速和减速3个阶段;当运动路径长度小于等于临界值时,运输设备做第Ⅱ类运动,经历加速、减速两个阶段。根据基本位移公式,堆垛机在两个方向上达到额定速度所需的临界距离为
Slim (1) 结合运输货物的重量、地面摩擦力的影响以及货物的运输距离对堆垛机在运动过程中的运动特性进行分析,得出其在水平、垂直方向运行时的能耗计算公式如下。
1)水平方向。
当
{S_{\mathrm{x}}} > \dfrac{{v_{\mathrm{x}}^2}}{{2 {a_{\mathrm{x}}}}} + \dfrac{{v_{\mathrm{x}}^2}}{{2 {d_{\mathrm{x}}}}} 时:\begin{split} &\qquad {E_{\mathrm{x}}} = {E_{{\mathrm{xa}}}} + {E_{{\mathrm{xc}}}} + {E_{{\mathrm{xd}}}} = \left(m g {k_{\mathrm{r}}} + m {a_{\mathrm{x}}} {k_{\mathrm{n}}}\right) \left(\frac{{v_{\mathrm{x}}^2}}{{2 {a_{\mathrm{x}}}}}\right) + \left(m g {k_{{\mathrm{r}}}}\right)\cdot \\ & \left({S_{\mathrm{x}}} - \frac{{v_{\mathrm{x}}^2}}{{2 {a_{\mathrm{x}}}}} - \frac{{v_{\mathrm{x}}^2}}{{2 {d_{\mathrm{x}}}}}\right) + \left(m {d_{\mathrm{x}}} {k_{\mathrm{n}}} - m g {k_{\mathrm{r}}}\right) \left(\frac{{v_{\mathrm{x}}^2}}{{2 {d_{\mathrm{x}}}}}\right)。\end{split} (2) 当
{S_{\mathrm{x}}} \leqslant \dfrac{{v_{\mathrm{x}}^2}}{{2 {a_{\mathrm{x}}}}} + \dfrac{{v_{\mathrm{x}}^2}}{{2 {d_{\mathrm{x}}}}} 时:\begin{split} &\qquad {E_{\mathrm{x}}} = {E_{{\mathrm{xa}}}} + {E_{{\mathrm{xc}}}} + {E_{{\mathrm{xd}}}} = \left(m g {k_{\mathrm{r}}} + m {a_{\mathrm{x}}} {k_{\mathrm{n}}}\right) \left(\frac{{{S_{\mathrm{x}}} {a_{\mathrm{x}}} {d_{\mathrm{x}}}}}{{{a_{\mathrm{x}}^2} + {a_{\mathrm{x}}} {d_{\mathrm{x}}}}}\right) + \\& 0 + \left(m {d_{\mathrm{x}}} {k_{\mathrm{n}}} - m g {k_{\mathrm{r}}}\right) \left(\frac{{{S_{\mathrm{x}}} {a_{\mathrm{x}}} {d_{\mathrm{x}}}}}{{a_{_{\mathrm{x}}}^2 + {a_{\mathrm{x}}} {d_{\mathrm{x}}}}}\right)。 \end{split} (3) 2)垂直方向。
当
{S_{\mathrm{y}}} > \dfrac{{v_{\mathrm{y}}^2}}{{2 {a_{\mathrm{y}}}}} + \dfrac{{v_{\mathrm{y}}^2}}{{2 {d_{\mathrm{y}}}}} 时:\begin{split} & \qquad {E_{\mathrm{y}}} = {E_{{\mathrm{ya}}}} + {E_{{\mathrm{yc}}}} + {E_{{\mathrm{yd}}}} = \left(m g + m {a_{\mathrm{y}}} {k_{\mathrm{n}}}\right) \left(\frac{{v_{\mathrm{y}}^2}}{{2 {a_{\mathrm{y}}}}}\right) + \left(m g\right) \cdot \\ &\left({S_{\mathrm{y}}} - \frac{{v_{\mathrm{y}}^2}}{{2 {a_{\mathrm{y}}}}} - \frac{{v_{\mathrm{y}}^2}}{{2 {d_{\mathrm{y}}}}}\right) + \left(m g - m {d_{\mathrm{y}}}\right) \left(\frac{{v_{\mathrm{y}}^2}}{{2 {d_{\mathrm{y}}}}}\right)。 \end{split} (4) 当
{S_{\mathrm{y}}} \leqslant \dfrac{{v_{\mathrm{y}}^2}}{{2 {a_{\mathrm{y}}}}} + \dfrac{{v_{\mathrm{y}}^2}}{{2 {d_{\mathrm{y}}}}} 时:\begin{split} & \qquad {E_{\mathrm{y}}} = {E_{{\mathrm{ya}}}} + {E_{{\mathrm{yc}}}} + {E_{{\mathrm{yd}}}} = \left(m g + m {a_{\mathrm{y}}} {k_{\mathrm{n}}}\right) \left(\frac{{{S_{\mathrm{y}}} {a_{\mathrm{y}}} {d_{\mathrm{y}}}}}{{{a_{\mathrm{y}}^2} + {a_{\mathrm{y}}} {d_{\mathrm{y}}}}}\right) + \\ & 0 + \left(m g - m {d_{\mathrm{y}}}\right) \left(\frac{{{S_{\mathrm{y}}} {a_{\mathrm{y}}} {d_{\mathrm{y}}}}}{{d_{\mathrm{y}^2} + {a_{\mathrm{y}}} {d_{\mathrm{y}}}}}\right)。 \end{split} (5) 综上,堆垛机在水平、垂直方向运行时的总能耗目标函数公式为
\qquad \min {f_1} \left({E_{{\mathrm{all}}}}\right) = \sum\limits_{x = 1}^p {\sum\limits_{y = 1}^{{c}} {\sum\limits_{{\textit{z}} = 1}^q { \left({E_{\mathrm{x}}} + {E_{\mathrm{y}}}\right) } } } 。 (6) 2.3 同类产品空间聚合模型
在家电制造业的自动化立体仓库中,某些零件在产品中经常配合使用,例如,控制面板和其相应的按钮、显示屏等,这些相关的零件在仓库中需要靠近存放,以便于更高效的拣货和组装。本研究提出了同类产品空间聚合数学模型,将经常同时出现在订单中的零件归为一类,存放在相同或相近货位,不仅可有效提高拣货效率,还可以减少仓库内货物的运输路径,使堆垛机的运动距离更短,从而减少能耗。
将立体仓库中的货物划分为n个种类,每种类货物占用
{N_i} 个货位,相同类别的货位坐标为\left({x_{ij,}}{y_{ij,}}{{\textit{z}} _{ij}}\right) 。则同种类货物的平均坐标为\qquad {\lambda _i} = \frac{1}{{{N_i}}}\mathop \sum \limits_{j = 1}^{{N_i}} \left( {{x_{ij}},{y_{ij}},{{\textit{z}} _{ij}}} \right)。 (7) 全部货物中心坐标为
\qquad O = \frac{1}{n}\mathop \sum \limits_{i = 1}^n {\lambda _i} 。 (8) 计算同一种类货物的平均坐标到全部货物中心坐标的距离总和最短,即为同类产品空间聚合模型的优化函数,第2个目标函数的计算公式如下:
\begin{split} &\qquad \min {f_2} =\\ & \mathop \sum \limits_{{{i}} = 1}^{{n}}\sqrt {{{\left( {{\lambda _i}\left( x \right) - O\left( x \right)} \right)}^2} + {{\left( {{\lambda _i}\left( y \right) - O\left( y \right)} \right)}^2} + {{\left( {{\lambda _i}\left( {\textit{z}} \right) - O\left( {\textit{z}} \right)} \right)}^2}} 。 \end{split} (9) 2.4 货架稳定性模型
考虑到货物存放的安全问题,重型货物应放置在货架较下层,而轻型货物则应放置在货架较上层。即将每个货格中货物的总重量与其所在层数和货格高度的乘积相加,然后除以所有货格中货物总重量的总和。一方面保证了货物的安全摆放,防止货架的倾倒,另一方面遵守“上轻下重”原则,可以减少堆垛机升起或下降时所产生的能耗。
第3个目标函数计算公式为
\qquad \min {f_3} = \dfrac{{\displaystyle\sum\limits_{x = 1}^p {\displaystyle\sum\limits_{y = 1}^c {\displaystyle\sum\limits_{{\textit{z}} = 1}^q {m {\textit{z}} h} } } }}{{\displaystyle\sum\limits_{x = 1}^p {\displaystyle\sum\limits_{y = 1}^c {\displaystyle\sum\limits_{{\textit{z}} = 1}^q m } } }} 。 (10) 2.5 货位优化模型
在上述的货位分配模型函数公式中,目标函数式(6)在考虑堆垛机运动路径长度、速度、加速度等因素的影响下,保证货物存取时能耗最低;目标函数式(9)使得在货架中放入同类货物时能够放在相近货位,保证同类货物之间的相关性,同时使得巷道负载均衡;目标函数式(10)将入库货物按照质量“上小下大”的原则进行摆放,从而增强货架稳定性。
上述优化模型的3个目标之间存在相互冲突的情况,无法获得每个目标函数值的最优解。因此本文建立多目标模型,充分考虑到不同目标之间的相互影响和权衡关系,在多个相互制约的目标之间作出最优决策,更符合实际问题的需要。
2.6 约束条件
针对上述模型构建约束条件如下所示:
\qquad 1 \leqslant x \leqslant p \text{;} (11) \qquad 1 \leqslant y \leqslant c \text{;} (12) \qquad 1 \leqslant {\textit{z}} \leqslant q \text{;} (13) \qquad L \leqslant {S_{\mathrm{x}}} \leqslant Lc \text{;} (14) \qquad h \leqslant {S_{\mathrm{y}}} \leqslant h q \text{;} (15) \qquad I \left(x,y,{\textit{z}} \right) = 0 。 (16) 其中,式 (11) ~ (13)表示货物货位约束;式(14)表示货物运行水平距离约束;式 (15)表示货物运行垂直距离约束;式 (16)表示货位独占性,即货位分配时只考虑空置货位。
3. 改进的多目标鲸鱼优化算法
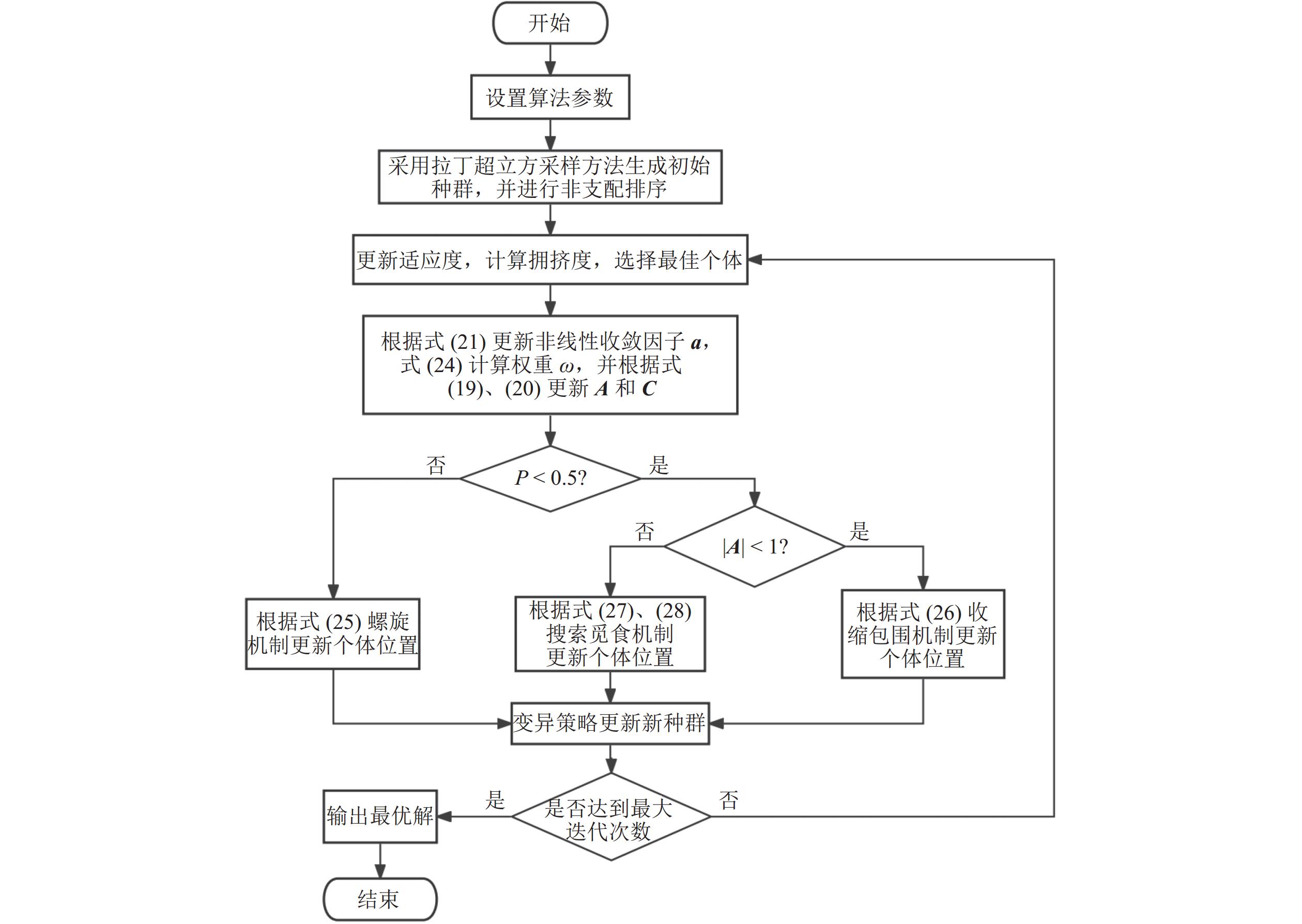
鲸鱼优化算法(whale optimization algorithm,WOA)是一种基于自然界中鲸鱼觅食行为的启发式优化算法,由Mirjalili等[14]于2016年提出。本文为解决多目标货位优化问题,将非支配排序与改进的WOA算法相结合,采用改进的多目标鲸鱼优化算法(INSWOA) 进行模型求解[15]。算法的整体流程如图2所示。
3.1 采用拉丁超立方采样方法初始化种群
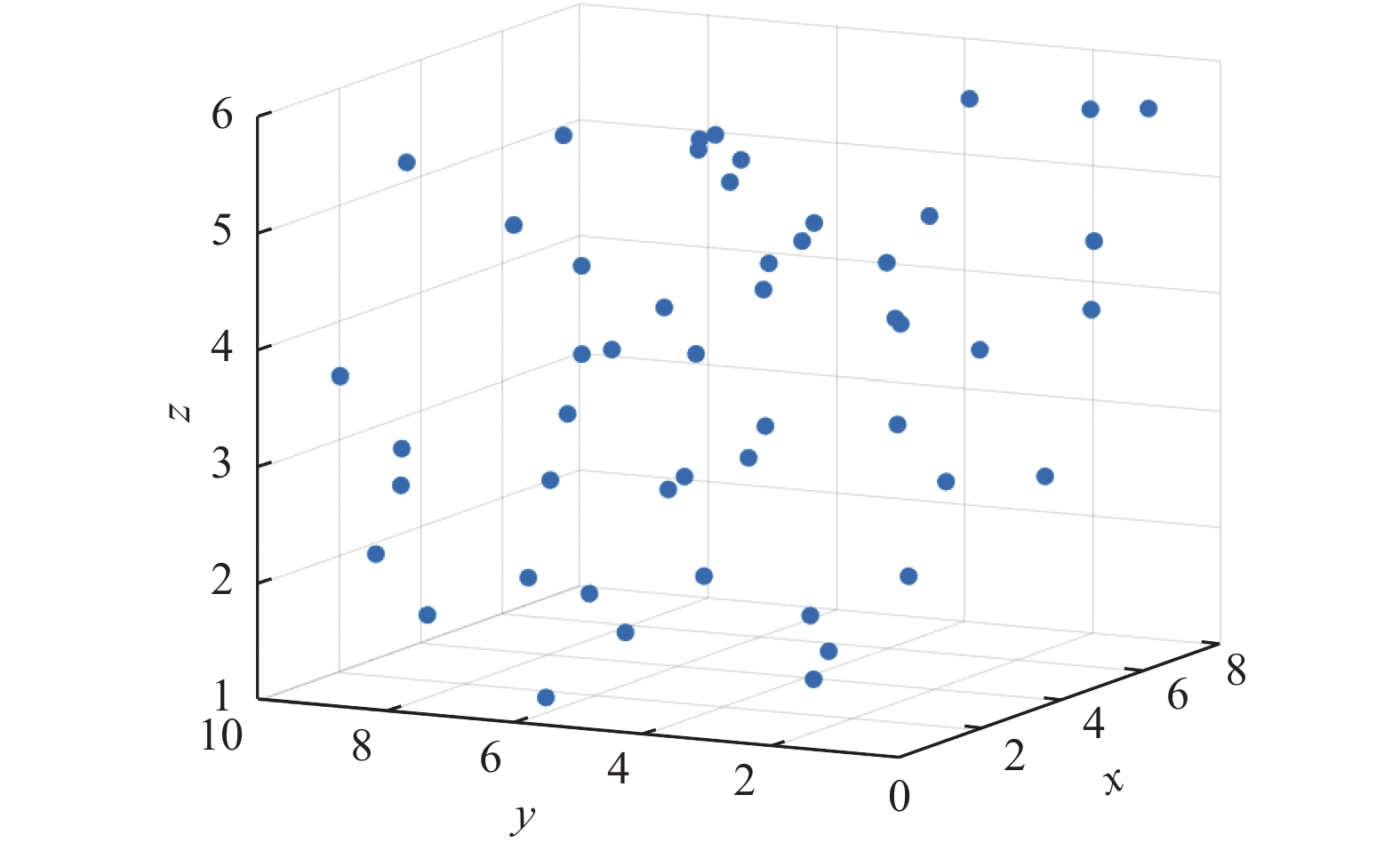
WOA以随机方式初始化种群,可能导致种群集中在搜索空间中的某些区域,增加了陷入局部最优解的风险。拉丁超立方体采样方法产生的初始种群位置,能够确保在每个维度上的采样点均匀分布,有助于覆盖整个搜索空间,确保全空间填充和抽样非重叠,从而使种群分布均匀。采样分布如图3所示。
3.2 非支配排序和拥挤度计算
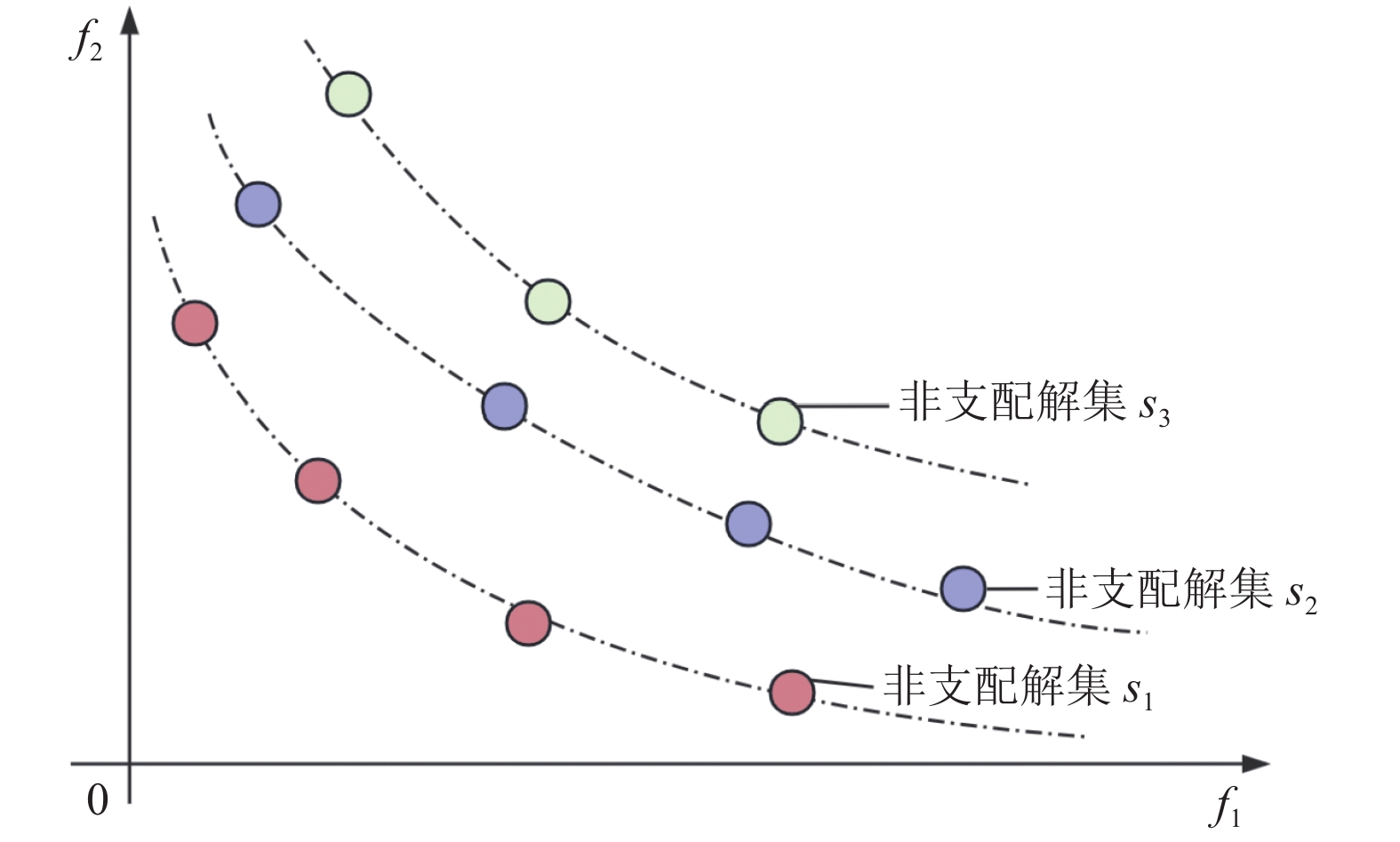
非支配排序是将种群个体根据Pareto支配关系进行分级的过程。首先,从种群中选出支配等级为1的Pareto解,即不被其他解支配的解;然后依次选出支配等级为2的解,直到完成整个种群的分级。支配等级越低的解优先支配等级较高的解,如图4所示。
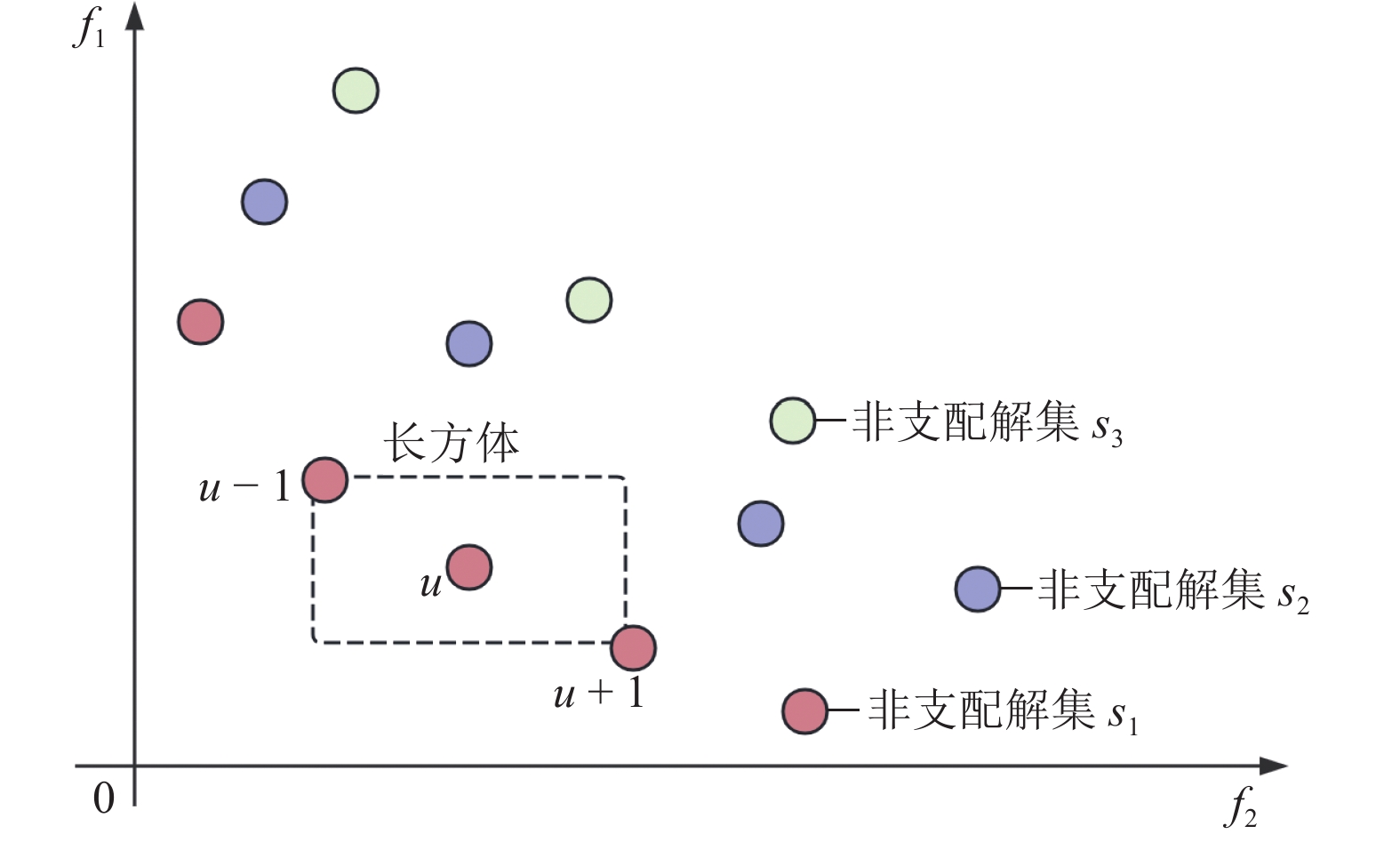
拥挤度是衡量解的稀疏程度的指标,定义为解与其邻域解之间所围成矩形的长度。以某一个体“u”为例,通过计算该个体与其邻域解 (“u−1”和“u+1”) 之间在目标维度上所围成矩形的长度,来衡量该个体的拥挤度。拥挤度越大,表示该解周围的解越稀疏。在多目标优化中,为了保持种群的多样性,选择拥挤度较大的解作为“最优个体”,以防止种群过度集中在某一区域。拥挤度计算示意图如图5所示。
3.3 收缩包围阶段
在收缩包围阶段,WOA算法通过分析猎物的位置来确定当前种群中的最佳候选解,其他鲸鱼个体会根据最优个体的位置不断更新自身位置。
收缩包围猎物的计算公式如下:
\qquad {{\boldsymbol{D}}_{{\mathrm{shrink}}}}{\boldsymbol{ = }}\left| {{\boldsymbol{CX}}^* {{ \left(t\right) }}{\boldsymbol{ - X}}{{ \left(t\right) }}} \right|; (17) \qquad {{\boldsymbol{X}}_{{\mathrm{shrink1}}}} \left({{{{t }}+ 1}}\right) {\boldsymbol{ = X}}^ * {{ \left({{t}}\right) }}{\boldsymbol{ - A}} \cdot {\boldsymbol{D}} ; (18) \qquad {\boldsymbol{A = }}2{\boldsymbol{\alpha }}{\boldsymbol{r}}{\boldsymbol{ - \alpha }}; (19) \qquad {\boldsymbol{C = }}2r 。 (20) 其中,
t 是当前的迭代次数,{\boldsymbol{A}} 和{\boldsymbol{C}} 是系数向量,{\boldsymbol{X}}^* \left(t\right) 是最优解的位置向量,{\boldsymbol{X}} \left(t\right) 是位置向量,{{\boldsymbol{D}}_{{\mathrm{shrink}}}} 是在收缩包围阶段鲸鱼与最优解之间的距离,{{\boldsymbol{X}}_{{\mathrm{shrink1}}}} \left({{t + 1}}\right) 是在收缩包围阶段经过t+1次迭代后鲸鱼的位置,{\boldsymbol{r}} 为[0,1]范围内的随机向量。WOA算法中{\boldsymbol{\alpha }} 表示系数向量,{\boldsymbol{\alpha }} 的值线性地从2下降至0,不利于算法的全局和局部搜索。因此,本文提出了一种非线性收敛因子,在迭代初期,该因子的值较大且收敛速度快,从而增强了算法的全局搜索能力。随着迭代的进行,收敛因子会非线性地逐渐降低且收敛速度减缓,增强了局部搜索能力[16]。其表达式如下:\qquad {\boldsymbol{\alpha }} = 2 - 2\sin \left( {\mu \frac{t}{{{t_{\max }}}}\text{π} } \right) 。 (21) 其中,
{t_{\max }} 为最大迭代次数,\mu 为取值为0.5的参数,在非线性收敛因子公式中参与计算,影响收敛因子的变化趋势。3.4 螺旋气泡网攻击阶段
螺旋更新策略通过在鲸鱼和猎物之间建立螺旋方式对座头鲸螺旋运动方式进行模拟,位置更新公式如下:
\qquad {\boldsymbol{D' = }}\left| {{\boldsymbol{X}}^ * \left(t\right) {\boldsymbol{ - X}} \left(t\right) } \right| ; (22) \qquad {{\boldsymbol{X}}_{{\mathrm{spiral1}}}} \left(t + 1\right) = {{\boldsymbol{D}}^{\boldsymbol{'}}} {{\mathrm{e}}^{bl}} \cos \left( {2\text{π} l} \right) + {\boldsymbol{X}}^* \left(t\right)。 (23) 其中,
{{\boldsymbol{X}}_{{\mathrm{spiral1}}}} \left(t + 1\right) 是在螺旋起泡网攻击阶段经过t+1次迭代后鲸鱼的位置,b 为对数螺旋形状的常量系数,l 为[−1,1]之间的随机数,{{\boldsymbol{D}}^{\boldsymbol{'}}} 为当前个体与目标个体间的距离向量。在WOA后期的局部开发阶段,算法容易陷入局部最优解并出现早熟收敛现象。为了保持种群的多样性并有效跳出局部最优解,本文依据文献[17-18]采用一种自适应权重策略。自适应权重策略表达式如下:\qquad \omega = 1 - \frac{{{{\mathrm{e}}^{\tfrac{t}{{{t_{\max }}}}}} - 1}}{{{\mathrm{e}} - 1}} ; (24) \qquad {{\boldsymbol{X}}_{{\mathrm{spiral2}}}} \left(t + 1\right) = {{\boldsymbol{D}}^{'}} \cdot {{\mathrm{e}}^{bl}} \cdot \cos \left( {2\text{π} l} \right) + \omega \cdot {\boldsymbol{X}} ^* \left(t\right); (25) \qquad {{\boldsymbol{X}}_{{\mathrm{shrink2}}}} \left(t + 1\right) = \omega \cdot {\boldsymbol{X}}^ * \left(t\right) - {\boldsymbol{A}} \cdot {\boldsymbol{D}} 。 (26) 其中,
{{\boldsymbol{X}}_{{\mathrm{spiral2}}}} \left(t + 1\right) 、{{\boldsymbol{X}}_{{\mathrm{shrink2}}}} \left(t + 1\right) 是在自适应权重调整后,经过t+1次迭代后鲸鱼的位置。3.5 搜索觅食阶段
在捕猎时,若
\left| {\boldsymbol{A}} \right| > 1 ,WOA将执行随机搜索觅食行为,此时,当前鲸鱼个体位置更新将通过随机选择另一只鲸鱼并向其靠近来实现,在这一阶段,鲸鱼个体将以较大的步长进行移动,以增强算法的全局搜索能力,该数学公式表示为:\qquad {{\boldsymbol{D}}_{{\mathrm{rand}}}} = \left| {{\boldsymbol{C}} \cdot {{\boldsymbol{X}}_{{\mathrm{rand}}}} \left(t\right) - {\boldsymbol{X}} \left(t\right) } \right| ; (27) \qquad {{\boldsymbol{X}}_{{\mathrm{rand}}}} \left(t + 1\right) = {{\boldsymbol{X}}_{{\mathrm{rand}}}} \left(t\right) - {\boldsymbol{A}} \cdot {\boldsymbol{D}} 。 (28) 其中,
{{\boldsymbol{D}}_{{\mathrm{rand}}}} 是搜索觅食阶段鲸鱼与最优解之间的距离,{{\boldsymbol{X}}_{{\mathrm{rand}}}} \left(t + 1\right) 是此阶段下经过t+1次迭代后鲸鱼的位置,{{\boldsymbol{X}}_{{\mathrm{rand}}}} 为随机选择的鲸鱼个体在当前种群中的位置。3.6 变异策略
在算法中加入变异策略以增强种群多样性,随机选择部分货位设计变量进行变异,生成新的解向量。然后计算其目标函数值,并用非支配排序检查新解与当前种群解的优劣。如果新解在所有目标上不劣于当前解,则替换当前解;否则,保留当前解。重复这一过程直至达到终止条件。
4. 仿真实验
4.1 参数设定
以某家电企业零部件立体仓库为研究对象,来验证本文提出的考虑能耗的多目标货位优化模型和INSWOA算法的有效性。仓库规模、货架信息等主要规格参数如表2所示。研究数据来源于某家电制造企业零部件仓库2024年6月的备料订单,该月为销售旺季,确保了数据的代表性和分析价值。通过仓库的WMS(warehouse management system,仓储管理系统),提取出零件的质量、货位及出库频率等关键信息。为深化研究,本文在对所有订单数据进行系统汇总与初步分析后,选取了出货频率排名前50的货物作为后续试验的主要对象。同时,为了更深入地探索货物间的关联性,将经常同时出现在订单中的零件归类整理,最终形成了包含5类货物的数据集,初始信息如表3所示。
表 2 立体仓库相关参数Table 2. Related parameters of the automated storage and retrieval system参数描述 数值 货架参数 总排数p 8排 总列数c 10列 总层数q 6层 货位参数 长L 1 m 宽w 1 m 高h 1 m 堆垛机运动参数 堆垛机水平运行额定速度{v_{\rm{x}}} 1.5 m/s 堆垛机垂直运行额定速度{v_{\rm{y}}} 1 m/s 堆垛机水平运行加速度{a_{\rm{x}}} 1 m/s2 堆垛机水平运行减速度{d_{\rm{x}}} 0.5 m/s2 堆垛机垂直运行加速度{a_{\rm{y}}} 0.5 m/s2 堆垛机垂直运行减速度{d_{\rm{y}}} 0.5 m/s2 滚动阻力系数{k_{\rm{r}}} 0.1 转动质量阻力系数{k_{\rm{n}}} 1.0 其他 重力加速度g 9.8 m/s2 表 3 入库货物订单信息及原始货位信息Table 3. Information of in-warehousing goods orders and original storage location分类 货物编号 质量/kg 原始货位 (x, y, z) 出库频率 分类 货物编号 质量/kg 原始货位 (x, y, z) 出库频率 Ⅰ 1 25 (3,8,2) 0.78 Ⅲ 26 38 (1,7,3) 0.85 Ⅰ 2 47 (4,6,6) 0.85 Ⅲ 27 24 (4,6,2) 0.79 Ⅰ 3 34 (3,2,2) 0.88 Ⅲ 28 36 (8,3,4) 0.87 Ⅰ 4 57 (6,4,5) 0.73 Ⅲ 29 70 (7,4,6) 0.85 Ⅰ 5 19 (1,6,1) 0.65 Ⅲ 30 59 (2,7,6) 0.84 Ⅰ 6 21 (7,1,1) 0.84 Ⅳ 31 66 (3,4,5) 0.71 Ⅰ 7 33 (4,10,3) 0.69 Ⅳ 32 17 (7,3,5) 0.80 Ⅰ 8 35 (3,6,5) 0.83 Ⅳ 33 26 (6,9,6) 0.75 Ⅰ 9 44 (5,9,4) 0.74 Ⅳ 34 39 (5,8,5) 0.83 Ⅰ 10 30 (8,7,2) 0.86 Ⅳ 35 41 (4,7,3) 0.76 Ⅱ 11 39 (1,5,4) 0.67 Ⅳ 36 53 (1,8,6) 0.89 Ⅱ 12 68 (4,2,5) 0.71 Ⅳ 37 27 (8,1,1) 0.74 Ⅱ 13 34 (7,10,3) 0.68 Ⅳ 38 64 (7,2,5) 0.82 Ⅱ 14 19 (8,9,2) 0.81 Ⅳ 39 39 (1,3,4) 0.73 Ⅱ 15 55 (6,3,4) 0.76 Ⅳ 40 18 (5,6,1) 0.81 Ⅱ 16 36 (4,8,1) 0.73 Ⅴ 41 69 (6,3,6) 0.82 Ⅱ 17 29 (2,4,2) 0.82 Ⅴ 42 46 (3,1,4) 0.77 Ⅱ 18 22 (7,3,2) 0.79 Ⅴ 43 79 (2,2,5) 0.85 Ⅱ 19 39 (5,6,2) 0.63 Ⅴ 44 37 (3,7,4) 0.65 Ⅱ 20 23 (3,5,1) 0.72 Ⅴ 45 55 (1,10,5) 0.72 Ⅲ 21 64 (6,10,6) 0.70 Ⅴ 46 29 (4,1,6) 0.68 Ⅲ 22 29 (2,5,1) 0.67 Ⅴ 47 18 (6,8,1) 0.69 Ⅲ 23 68 (3,9,4) 0.75 Ⅴ 48 38 (4,9,5) 0.75 Ⅲ 24 35 (4,4,1) 0.69 Ⅴ 49 51 (5,2,5) 0.83 Ⅲ 25 32 (8,1,3) 0.74 Ⅴ 50 77 (8,10,6) 0.66 4.2 模型仿真
使用Matlab 2022对已构建的货位分配模型进行优化仿真。此仿真共涉及3个目标函数:降低堆垛机总能耗、加强同类产品空间聚合、提高货架稳定性。将NSWOA (non-dominated sorting whale optimization algorithm,非支配排序鲸鱼优化算法) 和INSWOA算法进行对比分析。其中算法参数均设置一致,迭代500次后,所得到的Pareto解集如图6所示。
由图6可知,INSWOA算法不仅在整体解质量上超越NSWOA,还在能耗目标函数上有明显的改进,具体数值从50 000 ~ 100 000 J降至42 000 ~ 46 000 J,最高能效提升达到了约20%,实现了能耗的显著降低。
以上Pareto解集中任意两解均不为支配关系。图7为能耗目标函数与其他目标函数之间的关系。
由图7可见降低堆垛机能耗的目标函数与其他目标函数值之间存在一定的权衡关系,当优化能耗目标函数时,INSWOA算法能够保持其他目标函数的性能不变,且其他目标函数值均有一定程度的优化,表明其在三者之间达成了良好的平衡,实现了多目标的协调发展。
4.3 模型求解结果
对初始货位进行优化,程序运行结束后得到一组Pareto解集,去掉一些重复的解,得到最优Pareto解集如表4所示。
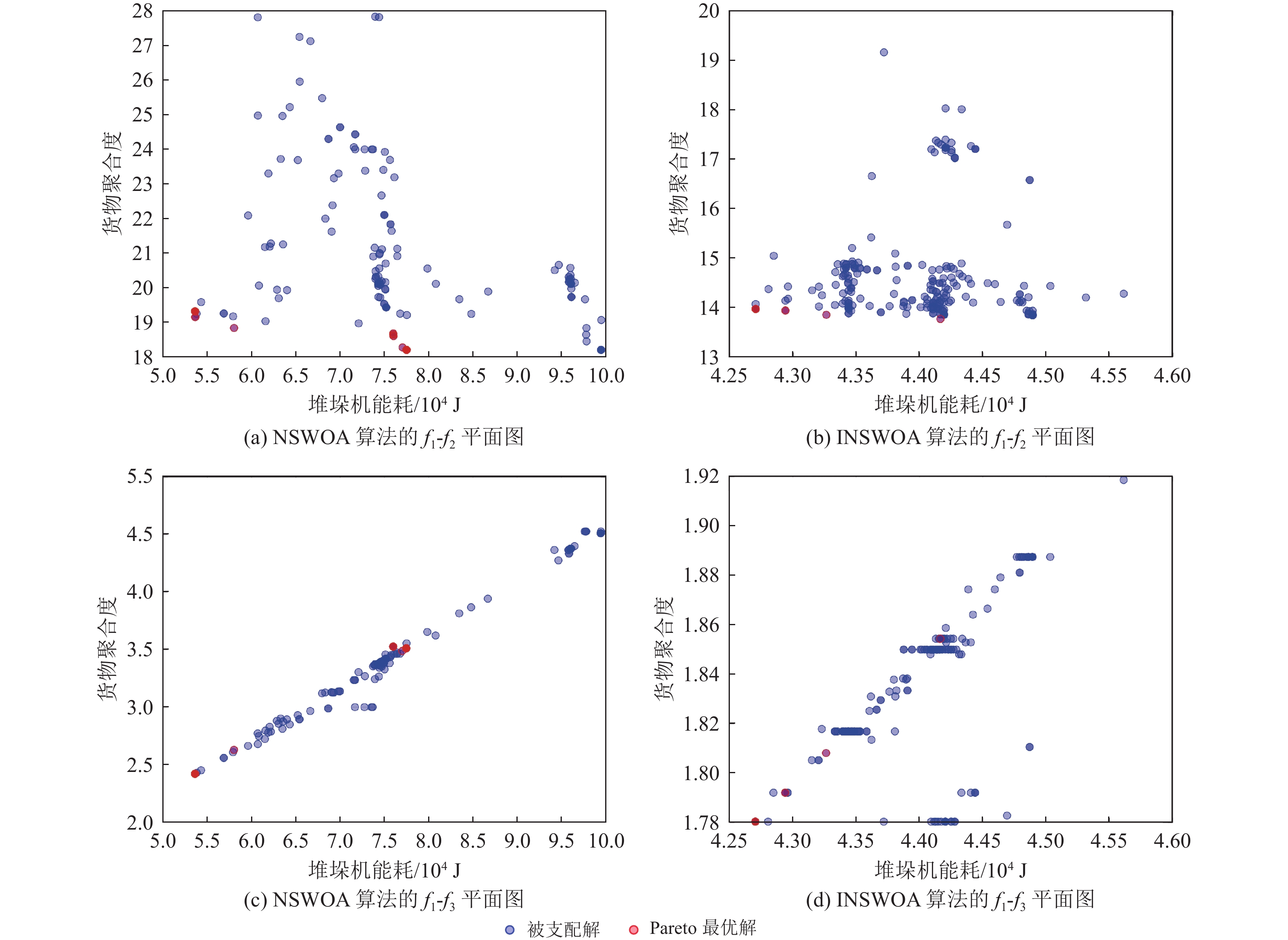
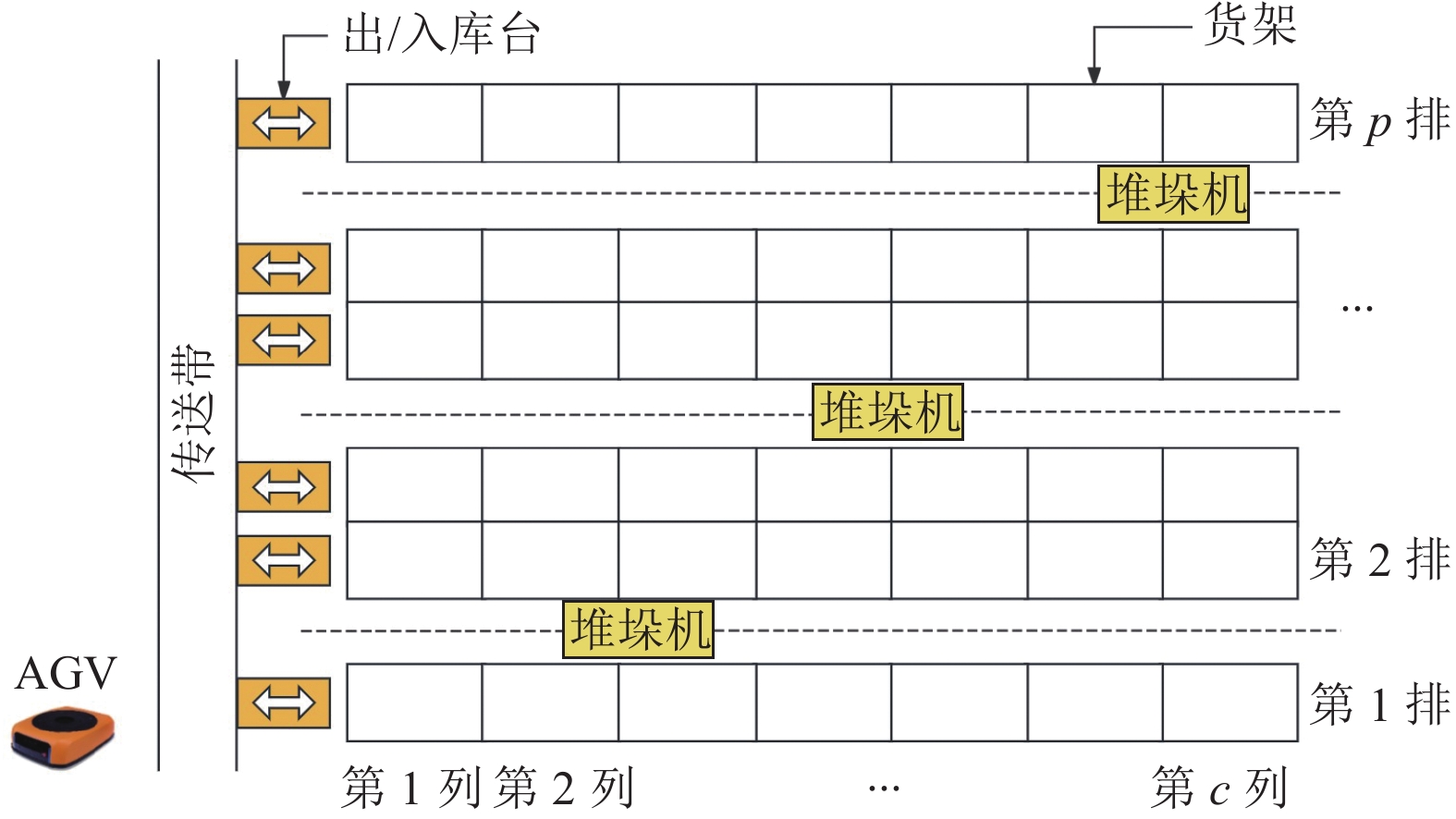
表 4 Pareto最优解集表Table 4. Table of Pareto optimal solution setPareto解集序号 堆垛机总能耗/J 货物空间聚合度 货架稳定性 1 44 249.54 12.10 1.89 2 44 174.08 12.39 1.89 3 43 831.08 12.41 1.87 4 42 991.22 13.29 1.82 5 44 163.82 13.76 1.85 6 43 262.22 13.85 1.80 7 42 938.82 13.94 1.79 8 42 703.62 13.97 1.78 9 44 173.10 14.65 1.81 10 44 168.20 14.66 1.81 11 44 131.94 14.79 1.81 12 44 122.14 15.04 1.81 13 44 116.26 15.06 1.81 14 44 100.58 15.13 1.81 15 44 031.00 15.15 1.81 16 44 006.50 15.29 1.81 17 43 960.44 15.48 1.80 18 43 715.44 15.71 1.79 1) 目标函数值的归一化。
\qquad f'_{ik} = \frac{{{f_{ik}} - f_{ik}^{\min }}}{{f_{ik}^{\max } - f_{ik}^{\min }}}。 (29) 式中:i表示Pareto解集中解的数量;
{f_{ik}} 表示第i个解在第k个目标上的值;f_{ik}^{\max } 表示在Pareto解集内第k个目标函数的最大值;f_{ik}^{\min } 表示在Pareto解集内第k个目标函数的最小值。经过归一化处理后的结果见表5。表 5 归一化处理后的目标函数值Table 5. Normalized objective function valuesPareto解集序号 堆垛机总能耗/J 货物空间聚合度 货架稳定性 1 1.000 0.000 1.000 2 0.951 0.080 1.000 3 0.729 0.086 0.818 4 0.186 0.330 0.364 5 0.945 0.460 0.636 6 0.361 0.485 0.182 7 0.152 0.510 0.091 8 0.000 0.518 0.000 9 0.951 0.706 0.273 10 0.947 0.709 0.273 11 0.924 0.745 0.273 12 0.918 0.814 0.273 13 0.914 0.820 0.273 14 0.904 0.839 0.273 15 0.859 0.845 0.273 16 0.843 0.884 0.273 17 0.813 0.936 0.182 18 0.655 1.000 0.091 2) 确定权重。
目标函数由3个子函数构成,权重的大小可以根据企业对于目标函数体现的存储策略的侧重程度灵活调整,由于在考虑能耗的货位优化模型中的核心优化目标是降低作业设备能耗,故为降低堆垛机作业能耗目标分配最大权重,以确保能源使用效率最大化,将f1权重设为0.63。将同类产品放置在靠近或相邻的位置可以提高存取效率,更有效地利用仓库空间,因此将f2分配较大权重,设为0.26。货架稳定性与降低能耗两个子目标均倾向于将货物存放较低的货架层,所以在货位优化时,为降低货架重心目标分配较小权重,将f3的权重设为0.11。这样的权重分配能够在主要优化目标是节省设备作业能耗的前提下,有效地平衡货物存取效率和操作空间的利用。
3) 目标加权值的计算。
求解Pareto解的综合目标值为
\qquad F = \sum\limits_{n = 1}^k {{\omega _n} {f_n}} 。 (30) 式中,F代表归一化后的目标函数加权值。通过式(30)可以计算出Pareto解加权后的目标综合值,如表6所示,其中,第8个解的加权值最小,因此该分配方案被确定为系统的最终优化结果,并用于后续分析。
表 6 加权后的目标综合值Table 6. Weighted comprehensive objective valuesPareto解集序号 目标综合值 1 0.740 2 0.730 3 0.572 4 0.243 5 0.785 6 0.374 7 0.238 8 0.135 9 0.813 10 0.811 11 0.806 12 0.820 13 0.819 14 0.818 15 0.791 16 0.791 17 0.776 18 0.682 优化后具体货位分配如表7所示。
表 7 优化后货位分配结果Table 7. Results of optimized storage location allocation货物编号 优化后货位 货物编号 优化后货位 1 (5,4,4) 26 (6,4,3) 2 (2,4,2) 27 (5,7,1) 3 (4,4,1) 28 (5,7,3) 4 (5,3,2) 29 (5,8,2) 5 (2,5,2) 30 (4,5,1) 6 (4,5,4) 31 (5,8,1) 7 (6,5,1) 32 (5,5,3) 8 (7,6,2) 33 (3,7,1) 9 (5,6,1) 34 (5,5,2) 10 (7,5,1) 35 (6,7,4) 11 (2,7,2) 36 (5,6,2) 12 (2,6,1) 37 (6,4,2) 13 (3,5,1) 38 (7,5,2) 14 (6,5,3) 39 (5,5,1) 15 (3,4,1) 40 (5,3,3) 16 (3,5,2) 41 (4,5,2) 17 (3,6,1) 42 (6,4,1) 18 (2,6,3) 43 (5,4,2) 19 (5,6,3) 44 (6,8,2) 20 (3,7,2) 45 (6,8,1) 21 (6,6,1) 46 (4,4,2) 22 (7,4,2) 47 (6,7,1) 23 (6,6,2) 48 (5,4,3) 24 (4,7,2) 49 (4,6,1) 25 (3,6,2) 50 (7,7,1) 优化前后货位分配仿真图如图8所示。
通过图8可以看出,优化前货物摆放混乱且同类货物分散,导致货架稳定性差、堆垛机行走距离长,进而影响了作业效率并增加了能耗。应用INSWOA算法进行货位分配后,货物显著集中于货架中间区域,从而提高了货架的稳定性,并显著缩短了堆垛机的行走距离,最终将能耗降低了51.96%。
表8显示,相比NSWOA算法,INSWOA算法在优化目标函数方面表现更佳,在保证能耗优化的同时,其他目标函数值均有明显优化,显示出INSWOA算法在降低能耗及多目标优化方面的显著优势。
表 8 优化前后各目标函数值对比情况Table 8. Comparison of objective function values before and after optimization目标函数 优化前 NSWOA INSWOA 优化后 降低值 优化百分比/% 优化后 降低值 优化百分比/% {f_1}/J 88 897.80 75 988.96 12 908.84 16.98 42 703.62 46 194.18 51.96 {f_2} 28.28 18.64 9.64 34.00 13.97 14.31 50.61 {f_3} 4.05 3.53 0.52 13.00 1.78 2.27 56.10 6. 结语
货位优化是一个多目标的优化过程,本文在考虑堆垛机运行路径长度、加速度、产品类别、货物质量等因素的基础上提出一种考虑能耗的多目标货位分配模型,使用了标准多目标鲸鱼优化算法和改进的多目标鲸鱼优化算法对模型求解。结果对比分析可得,本文提出的模型及算法在降低仓储能耗、增强同类产品空间聚合度以及提高货架稳定性3方面均表现出显著优势,有助于推动自动化立体仓库绿色化、高效化发展。
-
表 1 参数定义
Table 1 Parameter definitions
模型参数 定义 {E_{\mathrm{x}}}/J 堆垛机水平运行时能耗 {E_{{\mathrm{xa}}}}/J 堆垛机在水平方向进行加速运动时能耗 {E_{{\mathrm{xc}}}}/J 堆垛机在水平方向进行匀速运动时能耗 {E_{{\mathrm{xd}}}}/J 堆垛机在水平方向进行减速运动时能耗 {E_{\mathrm{y}}}/J 堆垛机垂直运行时能耗 {E_{{\mathrm{ya}}}}/J 堆垛机在垂直方向进行加速运动时能耗 {E_{{\mathrm{yc}}}}/J 堆垛机在垂直方向进行匀速运动时能耗 {E_{{\mathrm{yd}}}}/J 堆垛机在垂直方向进行减速运动时能耗 {v_{\mathrm{x}}}/ (m∙s−1) 堆垛机水平运行额定速度 {v_{\mathrm{y}}}/ (m∙s−1) 堆垛机垂直运行额定速度 g/ (m∙s−2) 重力加速度 {k_{\mathrm{r}}} 匀速状态下的滚动阻力系数 {k_{\mathrm{n}}} 非匀速状态下的转动质量阻力系数 {a_{\mathrm{x}}}/ (m∙s−2) 堆垛机水平运行加速度 {d_{\mathrm{x}}}/ (m∙s−2) 堆垛机水平运行减速度 {a_{\mathrm{y}}}/ (m∙s−2) 堆垛机垂直运行加速度 {d_{\mathrm{y}}}/ (m∙s−2) 堆垛机垂直运行减速度 p 货架的排数 c 货架的列数 q 货架的层数 L/m 单元货格的长度 w/m 单元货格的宽度 h/m 单元货格的高度 m/kg 货位为(x,y,z)的货物质量 o/m 全部货物的中心坐标 n 所有产品类别数 i 货物种类的索引,i \in [1,n] {\lambda _i}/m 货物种类i的平均中心坐标 {N_i} 第i类产品的个数,j \in [1,{N_i}] \left( {{x_{ij}},{y_{ij}},{{\textit{z}} _{ij}}} \right) /m 种类i下第j个货物的坐标 表 2 立体仓库相关参数
Table 2 Related parameters of the automated storage and retrieval system
参数描述 数值 货架参数 总排数p 8排 总列数c 10列 总层数q 6层 货位参数 长L 1 m 宽w 1 m 高h 1 m 堆垛机运动参数 堆垛机水平运行额定速度{v_{\rm{x}}} 1.5 m/s 堆垛机垂直运行额定速度{v_{\rm{y}}} 1 m/s 堆垛机水平运行加速度{a_{\rm{x}}} 1 m/s2 堆垛机水平运行减速度{d_{\rm{x}}} 0.5 m/s2 堆垛机垂直运行加速度{a_{\rm{y}}} 0.5 m/s2 堆垛机垂直运行减速度{d_{\rm{y}}} 0.5 m/s2 滚动阻力系数{k_{\rm{r}}} 0.1 转动质量阻力系数{k_{\rm{n}}} 1.0 其他 重力加速度g 9.8 m/s2 表 3 入库货物订单信息及原始货位信息
Table 3 Information of in-warehousing goods orders and original storage location
分类 货物编号 质量/kg 原始货位 (x, y, z) 出库频率 分类 货物编号 质量/kg 原始货位 (x, y, z) 出库频率 Ⅰ 1 25 (3,8,2) 0.78 Ⅲ 26 38 (1,7,3) 0.85 Ⅰ 2 47 (4,6,6) 0.85 Ⅲ 27 24 (4,6,2) 0.79 Ⅰ 3 34 (3,2,2) 0.88 Ⅲ 28 36 (8,3,4) 0.87 Ⅰ 4 57 (6,4,5) 0.73 Ⅲ 29 70 (7,4,6) 0.85 Ⅰ 5 19 (1,6,1) 0.65 Ⅲ 30 59 (2,7,6) 0.84 Ⅰ 6 21 (7,1,1) 0.84 Ⅳ 31 66 (3,4,5) 0.71 Ⅰ 7 33 (4,10,3) 0.69 Ⅳ 32 17 (7,3,5) 0.80 Ⅰ 8 35 (3,6,5) 0.83 Ⅳ 33 26 (6,9,6) 0.75 Ⅰ 9 44 (5,9,4) 0.74 Ⅳ 34 39 (5,8,5) 0.83 Ⅰ 10 30 (8,7,2) 0.86 Ⅳ 35 41 (4,7,3) 0.76 Ⅱ 11 39 (1,5,4) 0.67 Ⅳ 36 53 (1,8,6) 0.89 Ⅱ 12 68 (4,2,5) 0.71 Ⅳ 37 27 (8,1,1) 0.74 Ⅱ 13 34 (7,10,3) 0.68 Ⅳ 38 64 (7,2,5) 0.82 Ⅱ 14 19 (8,9,2) 0.81 Ⅳ 39 39 (1,3,4) 0.73 Ⅱ 15 55 (6,3,4) 0.76 Ⅳ 40 18 (5,6,1) 0.81 Ⅱ 16 36 (4,8,1) 0.73 Ⅴ 41 69 (6,3,6) 0.82 Ⅱ 17 29 (2,4,2) 0.82 Ⅴ 42 46 (3,1,4) 0.77 Ⅱ 18 22 (7,3,2) 0.79 Ⅴ 43 79 (2,2,5) 0.85 Ⅱ 19 39 (5,6,2) 0.63 Ⅴ 44 37 (3,7,4) 0.65 Ⅱ 20 23 (3,5,1) 0.72 Ⅴ 45 55 (1,10,5) 0.72 Ⅲ 21 64 (6,10,6) 0.70 Ⅴ 46 29 (4,1,6) 0.68 Ⅲ 22 29 (2,5,1) 0.67 Ⅴ 47 18 (6,8,1) 0.69 Ⅲ 23 68 (3,9,4) 0.75 Ⅴ 48 38 (4,9,5) 0.75 Ⅲ 24 35 (4,4,1) 0.69 Ⅴ 49 51 (5,2,5) 0.83 Ⅲ 25 32 (8,1,3) 0.74 Ⅴ 50 77 (8,10,6) 0.66 表 4 Pareto最优解集表
Table 4 Table of Pareto optimal solution set
Pareto解集序号 堆垛机总能耗/J 货物空间聚合度 货架稳定性 1 44 249.54 12.10 1.89 2 44 174.08 12.39 1.89 3 43 831.08 12.41 1.87 4 42 991.22 13.29 1.82 5 44 163.82 13.76 1.85 6 43 262.22 13.85 1.80 7 42 938.82 13.94 1.79 8 42 703.62 13.97 1.78 9 44 173.10 14.65 1.81 10 44 168.20 14.66 1.81 11 44 131.94 14.79 1.81 12 44 122.14 15.04 1.81 13 44 116.26 15.06 1.81 14 44 100.58 15.13 1.81 15 44 031.00 15.15 1.81 16 44 006.50 15.29 1.81 17 43 960.44 15.48 1.80 18 43 715.44 15.71 1.79 表 5 归一化处理后的目标函数值
Table 5 Normalized objective function values
Pareto解集序号 堆垛机总能耗/J 货物空间聚合度 货架稳定性 1 1.000 0.000 1.000 2 0.951 0.080 1.000 3 0.729 0.086 0.818 4 0.186 0.330 0.364 5 0.945 0.460 0.636 6 0.361 0.485 0.182 7 0.152 0.510 0.091 8 0.000 0.518 0.000 9 0.951 0.706 0.273 10 0.947 0.709 0.273 11 0.924 0.745 0.273 12 0.918 0.814 0.273 13 0.914 0.820 0.273 14 0.904 0.839 0.273 15 0.859 0.845 0.273 16 0.843 0.884 0.273 17 0.813 0.936 0.182 18 0.655 1.000 0.091 表 6 加权后的目标综合值
Table 6 Weighted comprehensive objective values
Pareto解集序号 目标综合值 1 0.740 2 0.730 3 0.572 4 0.243 5 0.785 6 0.374 7 0.238 8 0.135 9 0.813 10 0.811 11 0.806 12 0.820 13 0.819 14 0.818 15 0.791 16 0.791 17 0.776 18 0.682 表 7 优化后货位分配结果
Table 7 Results of optimized storage location allocation
货物编号 优化后货位 货物编号 优化后货位 1 (5,4,4) 26 (6,4,3) 2 (2,4,2) 27 (5,7,1) 3 (4,4,1) 28 (5,7,3) 4 (5,3,2) 29 (5,8,2) 5 (2,5,2) 30 (4,5,1) 6 (4,5,4) 31 (5,8,1) 7 (6,5,1) 32 (5,5,3) 8 (7,6,2) 33 (3,7,1) 9 (5,6,1) 34 (5,5,2) 10 (7,5,1) 35 (6,7,4) 11 (2,7,2) 36 (5,6,2) 12 (2,6,1) 37 (6,4,2) 13 (3,5,1) 38 (7,5,2) 14 (6,5,3) 39 (5,5,1) 15 (3,4,1) 40 (5,3,3) 16 (3,5,2) 41 (4,5,2) 17 (3,6,1) 42 (6,4,1) 18 (2,6,3) 43 (5,4,2) 19 (5,6,3) 44 (6,8,2) 20 (3,7,2) 45 (6,8,1) 21 (6,6,1) 46 (4,4,2) 22 (7,4,2) 47 (6,7,1) 23 (6,6,2) 48 (5,4,3) 24 (4,7,2) 49 (4,6,1) 25 (3,6,2) 50 (7,7,1) 表 8 优化前后各目标函数值对比情况
Table 8 Comparison of objective function values before and after optimization
目标函数 优化前 NSWOA INSWOA 优化后 降低值 优化百分比/% 优化后 降低值 优化百分比/% {f_1}/J 88 897.80 75 988.96 12 908.84 16.98 42 703.62 46 194.18 51.96 {f_2} 28.28 18.64 9.64 34.00 13.97 14.31 50.61 {f_3} 4.05 3.53 0.52 13.00 1.78 2.27 56.10 -
[1] 陈兴安, 吴超华, 王磊, 等. 包装行业自动化立体仓库货位分配方法研究[J]. 武汉理工大学学报, 2023, 45(4): 140-148. DOI: 10.3963/j.issn.1671-4431.2023.04.020 CHEN Xing'an, WU Chaohua, WANG Lei, et al. Research on storage location allocation method in automated stereoscopic warehouse of packaging industry[J]. Journal of Wuhan University of Technology, 2023, 45(4): 140-148. DOI: 10.3963/j.issn.1671-4431.2023.04.020
[2] 段剑峰, 李成群, 陈思. 基于自适应细菌觅食算法的立体仓库货位优化[J]. 制造业自动化, 2023, 45(5): 107-112. DUAN Jianfeng, LI Chengqun, CHEN Si. Optimization of storage locations in automated warehouse based on adaptive bacterial foraging algorithm[J]. Manufacturing Automation, 2023, 45(5): 107-112.
[3] 吴伟开, 何雪明, 黄育鹏. 基于海鸥算法的库区货位分配及优化研究[J]. 轻工机械, 2023, 41(4): 91-98. WU Weikai, HE Xueming, HUANG Yupeng. Research on storage location allocation and optimization in warehouse area based on seagull algorithm[J]. Light Industry Machinery, 2023, 41(4): 91-98.
[4] 李阳, 唐磊, 胡俊. 基于遗传算法的航天零件仓库货位优化研究[J]. 制造业自动化, 2020, 42(8): 68-73. LI Yang, TANG Lei, HU Jun. Research on storage location optimization of aerospace parts warehouse based on genetic algorithm[J]. Manufacturing Automation, 2020, 42(8): 68-73.
[5] 陈港生, 谢家翔, 付建林, 等. 一种多巷道立体仓库货位分配优化方法[J]. 机械工程师, 2023(12): 40-44. CHEN Gangsheng, XIE Jiaxiang, FU Jianlin, et al. An optimization method for storage location allocation in multi - lane automated storage and retrieval system[J]. Mechanical Engineer, 2023(12): 40-44.
[6] JIAO Y, XING X, ZHANG P, et al. Multi-objective storage location allocation optimization and simulation analysis of automated warehouse based on multi-population genetic algorithm[J]. Concurrent Engineering, 2018, 26(4): 367-377.
[7] YAN B, YAN C, LONG F, et al. Multi-objective optimization of electronic product goods location assignment in stereoscopic warehouse based on adaptive genetic algorithm[J]. Journal of Intelligent Manufacturing, 2018(29): 1273-1285.
[8] WAN Y, WANG S, HU Y, et al. Multiobjective optimization of the storage location allocation of a retail E-commerce picking zone in a picker-to-parts warehouse[J]. Engineering Letters, 2023, 31(2): EL_31_2_04.
[9] 王璐. 基于低碳经济环境的绿色物流管理策略研究[J]. 物流科技, 2024, 47(6): 43-45. WANG Lu. Research on green logistics management strategies in the context of a low - carbon economy[J]. Logistics Science and Technology, 2024, 47(6): 43-45.
[10] 冯心仪. 发展低碳物流的影响因素及对策[J]. 中国航务周刊, 2023(28): 65-67. FENG Xinyi. Influencing factors and countermeasures for the development of low - carbon logistics[J]. China Shipping Gazette, 2023(28): 65-67.
[11] REN Q, KU Y, WANG Y, et al. Research on design and optimization of green warehouse system based on case analysis[J]. Journal of Cleaner Production, 2023(388): 135998.
[12] 方磊, 吉卫喜, 彭威, 等. 动态储位分配策略下仓储作业能耗优化调度[J]. 计算机工程与应用, 2023, 59(4): 303-311. FANG Lei, JI Weixi, PENG Wei, et al. Energy - consumption - optimized scheduling of warehouse operations under dynamic storage location allocation strategy[J]. Computer Engineering and Applications, 2023, 59(4): 303-311.
[13] 夏绪辉, 朱强, 王蕾, 等. 考虑时间和能耗的立体仓库三维空间路径优化[J]. 武汉科技大学学报, 2018, 41(6): 465-472. XIA Xuhui, ZHU Qiang, WANG Lei, et al. Three - dimensional space path optimization of automated warehouse considering time and energy consumption[J]. Journal of Wuhan University of Science and Technology, 2018, 41(6): 465-472.
[14] MIRJALILI S, ANDREW L. The whale optimization algorithm[J]. Advances in Engineering Software, 2016(95): 51-67.
[15] JANGIR P, JANGIR N. Non-dominated sorting whale optimization algorithm (NSWOA): a multi-objective optimization algorithm for solving engineering design problems[J]. Global Journal of Research in Engineering, 2017, 14(4): 15-42.
[16] 武泽权, 牟永敏. 一种改进的鲸鱼优化算法[J]. 计算机应用研究, 2020, 37(12): 3618-3621. WU Zequan, MU Yongmin. An improved whale optimization algorithm[J]. Application Research of Computers, 2020, 37(12): 3618-3621.
[17] 尚猛, 康建英, 曹峻玮, 等. 基于改进鲸鱼优化算法的物流配送中心选址策略[J]. 计算机应用与软件, 2019, 36(6): 254-259. SHANG Meng, KANG Jianying, CAO Junwei, et al. Location - selection strategy of logistics distribution center based on improved whale optimization algorithm[J]. Computer Applications and Software, 2019, 36(6): 254-259.
[18] 褚鼎立, 陈红, 王旭光. 基于自适应权重和模拟退火的鲸鱼优化算法[J]. 电子学报, 2019, 47(5): 992-999. CHU Dingli, CHEN Hong, WANG Xuguang. Whale optimization algorithm based on adaptive weight and simulated annealing[J]. Acta Electronica Sinica, 2019, 47(5): 992-999.



 下载:
下载: